Zhang S., Yin H., Chen T., Huang Z., Cui L. and Zhang X. Graph embedding for recommendation against attribute inference attacks. In International World Wide Web Conferences (WWW), 2021.
概
利用差分隐私 (DP) 来作隐私保护的, 虽然标题强调了 graph embedding, 但是感觉所采用该的方法并不一定要局限在 graph embedding 上吧.
符号说明
- \(\mathcal{U}\), 用户;
- \(\mathcal{V}\), items;
- \(\mathcal{E}\), 用户和 items 之间的边, 当前进度 \(u, v\) 之间发生过交互二者之间才存在边, 且权重为 \(1\);
- \(\mathcal{G} = (\mathcal{U}, \mathcal{V}, \mathcal{E})\), 用户, items 所构成的二部图;
- \(\mathcal{N}(u)\), 那些和用户 \(u\) 产生过交互的 item \(v\) 的集合;
- \(\mathcal{N}(v)\), 那些和item \(v\) 产生过交互的 用户 \(u\) 的集合;
- \(\bm{x}_u = [\bm{x}_{(1)}, \bm{x}_{(2)} \cdots \bm{x}_{(d')}] \in [-1, 1]^{d_0}\), 用户 \(u\) 的其它的属性, 每一个 \(\bm{x}_{i}\) 表示一种属性 (一维的数值属性或者 one-hot 表示的 categorical 属性).
关于差分隐私 (differential privacy, DP) 可以看看 here. 这里按照文章的思路再重述一遍:
Differenttial privacy (DP)
\(\epsilon-\text{DP}\): 对于一个随机映射 \(f(\cdot)\) 而言, 如果对于任意集合 \(\mathcal{X}, \mathcal{X}', \rho(\mathcal{X}, \mathcal{X}') \le 1\) 以及任意可能的输出子集 \(O\) 有
\[\tag{1}
\mathbb{P}[f(\mathcal{X}) \in O] \le \exp(\epsilon) \mathbb{P}[f(\mathcal{X}') \in O]
\]
成立, 则称 \(f(\cdot)\) 是 \(\epsilon-\text{DP}\) 的. 注意这里 \(\rho(\mathcal{X}, \mathcal{X}') \le 1\) 表示两个集合距离最多为 1.
比如, \(\mathcal{X}, \mathcal{X}'\) 是两个仅有一个元素不同的两个数据集, 倘若模型随机函数 \(f(\cdot)\) 不符合 (1) 的定义, 那么说明这个元素是特殊的, 那么很有可能可以通过模型的输出来判断这个元素的一些信息, 从而导致信息的泄露.
Local DP
\(\epsilon-\text{LDP}\): 对于任意两个用户 \(u, u'\) 的两条交互数据 \(t, t'\), 若 \(f(\cdot)\)
\[\mathbb{P}[f(t) = t^*] \le \exp(\epsilon) \cdot \mathbb{P} [f(t') = t^*]
\]
对于任意的 \(t^*\) 成立, 则称 \(f(\cdot)\) 关于用户 \(u, u'\) 是 \(\epsilon-\text{LDP}\) 的.
主要内容
GNN 的流程
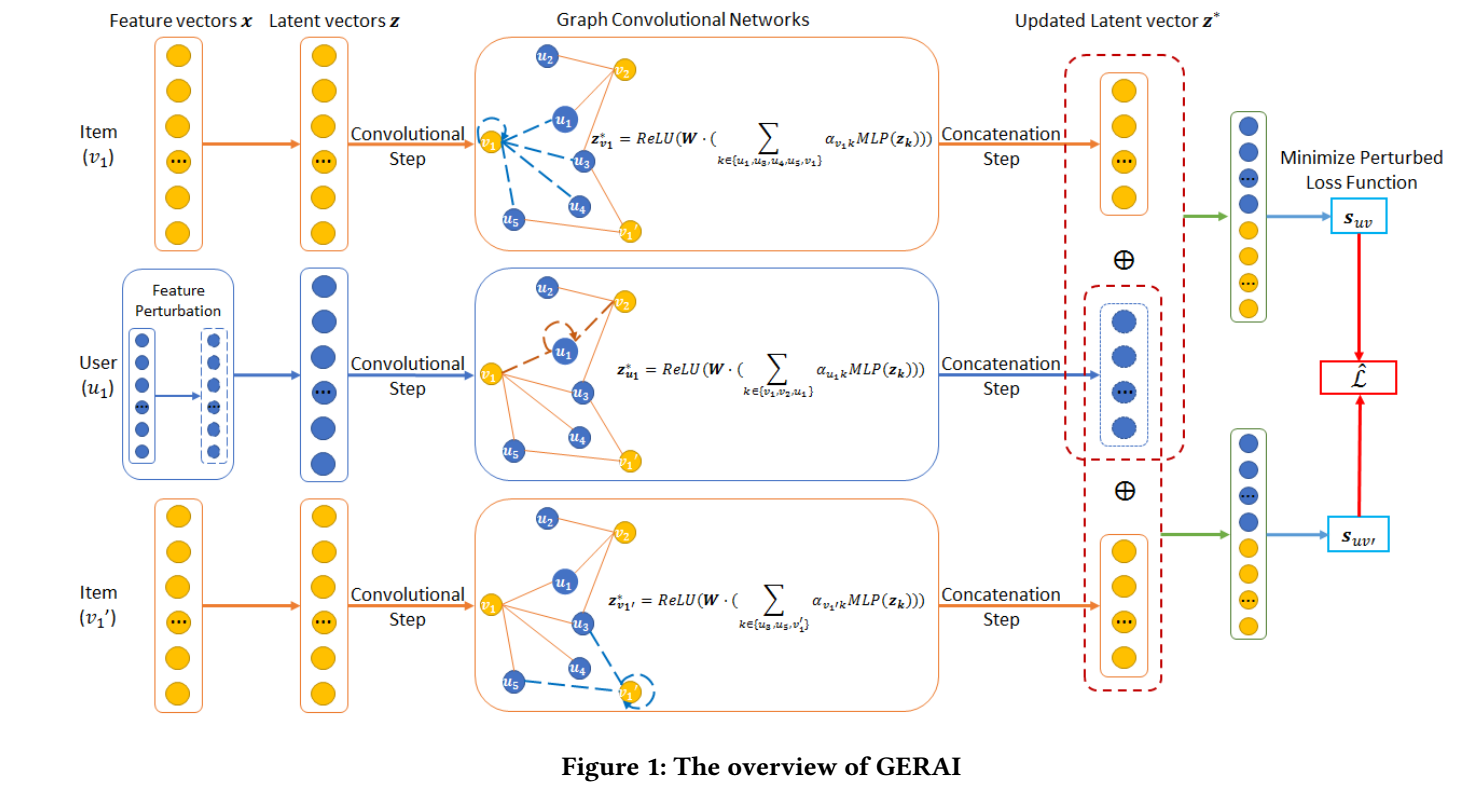
-
通过 embedding layer 得到用户和 items 的隐变量: \(\bm{z}_u, \bm{z}_v\);
-
接下来, 每一层按照图网络的方式进行特征提取:
\[\bm{z}_{u} = \text{ReLU}(W \cdot (\sum_{k \in \mathcal{N}(u) \cup \{u\}} \alpha_{uk} \text{MLP}(\bm{z}_k)) + \bm{b});
\]
\[\bm{z}_{v} = \text{ReLU}(W \cdot (\sum_{k \in \mathcal{N}(v) \cup \{v\}} \alpha_{kv} \text{MLP}(\bm{z}_k)) + \bm{b});
\]
其中 \(\alpha\) 是通过 attention network 得到的;
-
对用户和 items 提取两两的特征 (看文中的意思, 似乎上面只有一层?):
\[\bm{q}_{uv} = \text{ReLU} (W_3 (\bm{z}_u \oplus \bm{z}_v) + \bm{b}_3), \: u \in \mathcal{U}, v \in \mathcal{V};
\]
- 计算预测得分:
\[s_{uv} = \bm{h}^T \bm{q}_{uv};
\]
- 通过 BPR 进行训练:
\[\mathcal{L} = \sum_{(u, v, v') \in \mathcal{D}} -\log \sigma(s_{uv} - s_{uv'}) + \gamma \|\Theta\|^2,
\]
其中 \((u, v) \in \mathcal{E}, (u, v') \not \in \mathcal{E}\).
隐私保护
接下来我们讨论如何进行隐私保护.
这里, 我们希望对输入特征阶段进行扰动, 并希望:
\[\hat{x} := f(x)
\]
满足 \(\epsilon-\text{LDP}\).
首先我们讨论 \(x\) 为数值特征的情况, 然后再推广到 categorical 的和多维的 \(\bm{x}\).

算法 1 给出了扰动流程, 其中
\[C = \frac{\exp(\frac{\epsilon}{2}) + 1}{\exp(\frac{\epsilon}{2}) - 1}, \\
l(x) = \frac{C + 1}{2} x - \frac{C - 1}{2}, \\
\pi(x) = \ell(x) + C - 1. \\
\]
此时
\[\mathbb{P}[\hat{x} = c | x] =
\left \{
\begin{array}{ll}
p & \text{if } c \in [ \ell(x), \pi(x)] \\
\frac{p}{\exp(\epsilon)} & \text{if } c \in [-C, \ell(x)) \cup (\pi(x), C].
\end{array}
\right .
\]
其中
\[p = \frac{\exp(\epsilon / 2)}{\exp(\epsilon / 2) + 1}.
\]
则有以下结论成立:
Lemma 4.1: 算法1所定义的 \(\hat{x}\) 满足 \(\epsilon-\text{LDP}\).
proof: 显然, 当两个概率相同的时候是平凡的, 只需考虑:
\[\mathbb{P}(\hat{x} = c | x) \not = \mathbb{P}(\hat{x}=c|x')
\]
的时候, 此时
\[\frac{\mathbb{P}(\hat{x} = c | x)}{\mathbb{P}(\hat{x} = c | x')} \le \max(\exp(\epsilon), \exp(-\epsilon)) \le \exp(\epsilon).
\]
注意, 因为 \(x \in [-1, 1]\), 故 \(\hat{x} \in [-C, C]\).
接下来推广到更加一般的情况:

算法 2 对 \(\zeta < d'\) 个属性进行扰动, 由下列式子决定
\[(2)
\zeta = \max\{1, \min\{d', \lfloor \frac{\epsilon}{2.5} \rfloor \}\},
\]
然后保证每个属性都是 \(\frac{\epsilon}{\zeta}-\text{LDP}\)的.
对于 categorical 属性, 可以发现
\[\mathbb{P}[\hat{x}_{(i)} = \bm{c}| \bm{x}_{(i)}] \le \exp(\epsilon/ \zeta) \cdot
\mathbb{P}[\hat{x}_{(i)} = \bm{c}| \bm{x}_{(i)}']
\]
的左端项为:
\[\frac{1}{2} \cdot (1 - \frac{1}{\exp(\frac{\epsilon}{\zeta}) + 1})^{k} (\frac{1}{\exp(\frac{\epsilon}{\zeta}) + 1})^{d^{(i)} - 1 - k},
\]
其中 \(k\) 表示 \(\bm{c}\) 保持 \(0\) 的部分,
右端(最小)为:
\[\frac{\exp(\epsilon / \zeta)}{2} (1 - \frac{1}{\exp(\frac{\epsilon}{\zeta}) + 1})^{k - 1} \cdot (\frac{1}{\exp(\frac{\epsilon}{\zeta}) + 1})^{d^{(i)} - k}.
\]
二者相除可得: \(1\).
故 (2) 必成立.
下面, 综合来看由下面性质成立:
Lemma4.2: 算法 2 满足 \(\epsilon-\text{LDP}\).
proof:
\[\begin{array}{ll}
\mathbb{P}(\hat{\bm{x}} = \bm{t}|\bm{x})
&= \prod_i \mathbb{P}(\hat{\bm{x}}_{(i)}=\bm{t}_{(i)}|\bm{x}_{(i)}) \\
&\le \prod_i \exp(\frac{\epsilon}{\zeta}) \mathbb{P}(\hat{\bm{x}}_{(i)}=\bm{t}_{(i)}'|\bm{x}_{(i)}) \\
&\le \exp(\epsilon) \prod_i \mathbb{P}(\hat{\bm{x}}_{(i)}=\bm{t}_{(i)}'|\bm{x}_{(i)}) \\
&\le \exp(\epsilon) \mathbb{P}(\hat{\bm{x}} = \bm{t}|\bm{x}').
\end{array}
\]
注: 在用连乘号地方有点不严谨, 但愿能理解.
Optimization Stage
作者认为上面的操作不可避免地降低了模型的拟合能力. 作者希望通过设计一个 \(\mathcal{\tilde{L}}\) 来逼近 \(\mathcal{L}\), 且比较容易满足 \(\epsilon-\text{DP}\).
我们知道, \(\mathcal{L}\) 的一个泰勒展开为 (把 \(\sigma(\cdot)\) 中的看成自变量):
\[\mathcal{L} =\sum_{(u, v, v') \in \mathcal{D}} \sum_{j=0}^{\infty} \frac{f^{(k)}(0)}{k!} (\bm{h}^T \bm{q}_{uv} - \bm{h}^T \bm{q}_{uv'})^j,
\]
这里
\[f(x) = -\log \sigma(x) \rightarrow f(0) = \log 2, f'(0) = -\frac{1}{2}, f''(0) = \frac{1}{4}.
\]
我们用前三阶来近似 \(\mathcal{L}\), 即
\[\mathcal{\tilde{L}} = \sum_{(u, v, v') \in \mathcal{D}} \sum_{j=0}^{2} \frac{f^{(k)}(0)}{k!} (\bm{h}^T \bm{q}_{uv} - \bm{h}^T \bm{q}_{uv'})^j.
\]
我们考察在两个不同的 \(\mathcal{D}, \mathcal{D}'\) 下, 且 \(\mathcal{D}, \mathcal{D}'\) 之间仅有一个元素不同. 此时会导致存在 \(\bm{q}, \bm{q}'\) 不同.
\[\Delta := \max_{\mathcal{D}, \mathcal{D}'} \|\mathcal{\tilde{L}} (\mathcal{D})
-\mathcal{\tilde{L}} (\mathcal{D}')\|_1
\]
的一个大小.
我们假设 \(\bm{p}_{uv} \in (0, 1)^d\) (可以通过 clip 或激活函数 实现). 则
\[\begin{array}{ll}
\Delta &= \max_{\mathcal{D}, \mathcal{D}'} \|\mathcal{\tilde{L}} (\mathcal{D})
-\mathcal{\tilde{L}} (\mathcal{D}')\|_1 \\
&\le \max_{\bm{q}, \bm{q}'} \{ \|f'(0) \bm{h}^T (\bm{q} - \bm{q}') + \frac{f''(0)}{2} [\bm{h}^T (\bm{q} - \bm{q}')]^2\|_1 \} \\
&\le \max_{\bm{q}, \bm{q}'} \{ \|f'(0) \bm{h}^T (\bm{q} - \bm{q}')\|_1 + \|\frac{f''(0)}{2} [\bm{h}^T (\bm{q} - \bm{q}')]^2\|_1 \} \\
&\le \frac{\|\bm{h}\|_1}{2} + \frac{\|\bm{h}\|_1^2}{8}.
\end{array}
\]
注: 不好意思, 我不知道作者是不是在证明的时候给了 \(\bm{h}\) 也有什么额外的假设, 这里给出的结论是 \(\Delta \le d + \frac{d^2}{4}\), 不过没有什么关系, 因为我们只需要找到 \(\Delta\), 之后就可以通过此来定义合适的扰动方式.
最后, 实际上我们只需要令
\[\mathcal{\hat{L}} := \mathcal{\tilde{L}} + r, \; r \sim \text{Lap}(0, \sigma):= \frac{\sqrt{2}}{2\sigma} \exp(-\frac{\sqrt{2} |r|}{\sigma}).
\]
其中
\[\sigma = \sqrt{2}\Delta / \epsilon.
\]
此时我们可以发现:
\[\begin{array}{ll}
\frac{\mathbb{P}[\mathcal{\hat{L} = z}|\mathcal{D}]}{\mathbb{P}[\mathcal{\hat{L}} = z | \mathcal{D}']}
&=\frac{\mathbb{P}[r = z - \mathcal{\hat{L}}(\mathcal{D})]}{\mathbb{P}[r = z - \mathcal{\hat{L}} (\mathcal{D}')]} \\
&=\frac{\exp[-|z - \mathcal{\hat{L}}(\mathcal{D})| / \sigma]}{\exp[-|z - \mathcal{\hat{L}} (\mathcal{D}') | / \sigma]} \\
&= \exp(\frac{\sqrt{2}(|z - \mathcal{\hat{L}}(\mathcal{D}')|-|z - \mathcal{\hat{L}}(\mathcal{D}')|)}{\sigma}) \\
&\le \exp(\frac{\sqrt{2}|\mathcal{\hat{L}}(\mathcal{D})- \mathcal{\hat{L}}(\mathcal{D}')|}{\sigma}) \\
&= \exp(\frac{\sqrt{2} \epsilon |\mathcal{\hat{L}}(\mathcal{D})- \mathcal{\hat{L}}(\mathcal{D}')|}{\sqrt{2}\Delta}) \\
&\le \exp(\epsilon).
\end{array}
\]
不过需要注意的是, 作者是在多项式逼近 \(\mathcal{\hat{L}}\) 的系数上添加扰动的, 我感觉思路是大差不差的, 这里就不多说了.

问题
- 正如开头说的, 作者提出的方法似乎是通用的, 并不局限在一般的 graph embedding 上;
- 看实验, 在两个阶段都添加扰动效果是最好的, 问题是都用了拟合效果不更加就不好了? 凭借对损失的扰动也没看出来有啥特别辅助学习的作用啊.






 浙公网安备 33010602011771号
浙公网安备 33010602011771号