FairRec: Fairness-aware News Recommendation with Decomposed Adversarial Learning
概
本文针对新闻推荐过程中的性别 bias 问题进行剖析, 设计了一个框架用于解耦 bias-aware 和 bias-free embeddings.
符号说明
- \(u\), 用户;
- \(z\), 用户的某个属性;
- \(U\), 总共的用户的数量;
- \(\mathcal{D} = \{D_1, \cdots, D_N\}\), 用户历史点击的新闻;
- \(\mathcal{D}^c = \{D_1^c, D_2^c, \cdots, D_M^c\}\), 候选推荐新闻;
- \([y_1, \cdots, y_M]\), ground-truth labels (是否点击);
- \([\hat{y}_1, \cdots, \hat{y}_M]\), 预测的标签;
- \(\mathcal{D}^r = \{D_{i_1}^c, D_{i_2}^c, \cdots, D_{i_K}^c\}\), top-K 的一个推荐结果;
主要内容
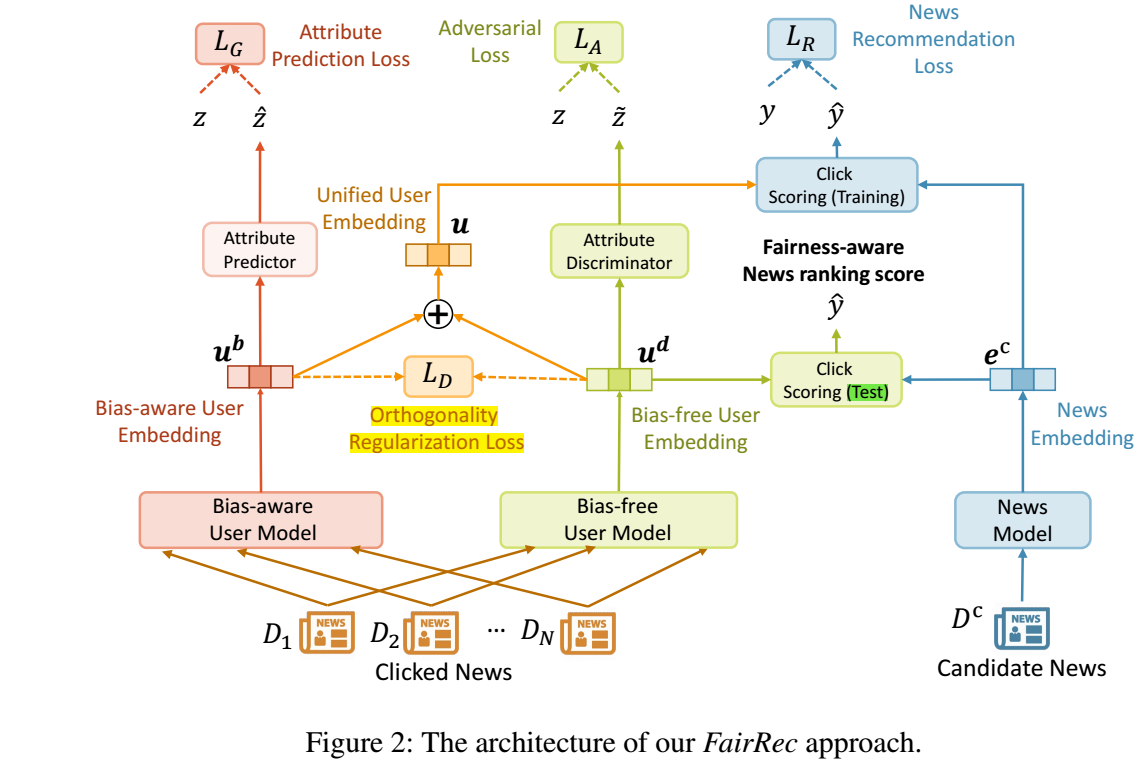
作者认为, 传统的新闻推荐系统会倾向于推荐给女性用户关于时尚类的新闻, 而对于男性用户推荐体育类的新闻, 这说明其中存在着性别的 bias. 作者希望学习 bias-free embeddings 来解决这一问题.
注: 个人认为, 其实这个算不得什么 bias, 或者说有什么不合理的地方. 只是, 新闻推荐系统有了这种倾向之后, 可能会忽视掉一部分喜欢体育的女性用户的利益和喜欢时尚的男性用户的利益. 我感觉作者对于框架的设计也并没有完全符合本文的出发点.
作者的框架流程大致如下:
- 用户的历史信息通过 bias-aware user model 得到 \(\bm{u}^b\);
- 用户的历史信息通过 bias-free user model 得到 \(\bm{u}^d\);
- 候选的新闻通过 news model 得到 \(\bm{e}^c\);
- 为了保证 \(\bm{u}^b\) 是 bias-aware 的, 自然地通过此能够反推出性别, 即我们可以设计一个属性预测器 (attribute predictor):
\[\hat{z} = \text{softmax}(W^b \bm{u}^b + \bm{b}^b),
\]
并最小化如下损失进行训练:
\[\mathcal{L}_G = -\frac{1}{U} \sum_{j=1}^U \sum_{i=1}^C z_i^j \log (\hat{z}_i^j);
\]
- 为了保证 \(\bm{u}^d\) 是 bias-free 的, 那么应当很难从特征 \(\bm{u}^d\) 中推测出性别来, 于是构建一个属性判别器 (attribute discriminator):
\[\tilde{z} = \text{softmax} (W^d \bm{u}^d + \bm{b}^d),
\]
按照对抗的方式训练二者, 如果没理解错的化, 就是希望判别器最小化 (同时bias-free user model 最大化) 如下损失:
\[\mathcal{L}_A = -\frac{1}{U} \sum_{j=1}^U \sum_{i=1}^C z_i^j \log (\tilde{z}_i^j);
\]
- 仅仅通过 5 并不能够很好地保证 \(\bm{u}^d\) 不隐含性别信息, 故额外引入正交正则化:
\[\mathcal{L}_D = \frac{1}{U} \sum_{i=1}^U \frac{|\bm{u}_i^b \cdot \bm{u}_i^d|}{\|\bm{u}_i^b\| \|\bm{u}_i^d\|};
\]
- 但实际上, \(\bm{u}^b, \bm{u}^d\) 对于准确的推荐都是十分重要的, 所以训练的时候基于
\[\mathcal{L}_R = -\frac{1}{N_c} \sum_{i=1}^{N_c} \log [\frac{\exp(\hat{y}_i)}{\exp(\hat{y}_i) + \sum_{j=1}^T \exp(\hat{y}_{i,j})}],
\]
其中 \(\hat{y} = \bm{u}_i \cdot \bm{e}^c\), \(\hat{y}_{i,j}\) 是相对于 \(\hat{y}_{i}\) 的负样本. \(N_c\) 是所有的点击过的候选新闻的个数.
- 最后总的损失:
\[\mathcal{L} = \mathcal{L}_R + \lambda_G \mathcal{L}_G + \lambda_D \mathcal{L}_D - \lambda_A \mathcal{L}_A.
\]
作者建议 \(\lambda_G = \lambda_D = \lambda_A = 0.5\).
- 在推断的时候, 倘若希望撇去性别的 bias, 可以通过
\[\bm{u}^d \cdot \bm{e}^c
\]
进行评估.
注: 上面流程只是拿性别举个例子, 并非限定在其中.
个人感觉虽然这么训练是尚可的, 但是在推断过程中相当于是完全阻断了性别等因素的影响, 好吗? 其次, 如何保证训练的时候, 不会过度依赖 \(\bm{u}^b\) 而导致 \(\bm{u}^d\) 缺乏评估性能呢?
代码
[code]


