CPFair: Personalized Consumer and Producer Fairness Re-ranking for Recommender Systems

目录

• 概
• 符号说明
  • 产品侧的 fairness: exposure and relevance
  • 用户侧的 fairness
  • 两侧的 fairness
• 主要内容

Naghiaei M., Rahmani H. A. and Deldjoo Y. CPFair: personalized consumer and producer fairness re-ranking for recommender systems. In International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR), 2022.

概

现在的一些推荐系统大抵以推荐效率为指标, 因而可能会造成用户或者产品的不公平对待 (bias). 有一些工作以及注意到了这一点, 并对用户或者产品的 fairness 进行了考虑, 但是很少有兼顾二者的. 但是有些时候兼顾二者的算法是必不可少的, 比如嘀嘀打车, 既要考虑到乘客的利益, 同时也不能忽视司机的利益. 本文主要提出一种后处理的方法解决这一问题.

符号说明

• \(\mathcal{U}, |\mathcal{U}| = n\), 用户;
• \(\mathcal{I}, |\mathcal{I}| = m\), 产品;
• \(L_N(u)\), 推荐系统对于用户 \(u\) 给出的 top-N 的一个推荐结果;
• \(s \in \mathcal{S}^{n \times N}\), 相应的 scores;
• \(L_K^F(u) \subset L_N(u)\), 在考虑 fairness 之后给出的一个综合的 top-K 的推荐结果, \(K \le N\);
• \(A = [A_{ui}]_{n \times N}\), 如果\(L_N(u)\) 中的第 \(i\) 个 item 依旧被 \(L_K^F(u)\) 推荐, 则 \(A_{ui} = 1\), 否则为 \(A_{ui} = 0\);

产品侧的 fairness: exposure and relevance

影响产品侧的公平性的主要因素就是不同类型产品之间的一个曝光率的差别. 将产品根据流行度可以划分为: short-hand \(\mathcal{I}_{1}\), long-tail \(\mathcal{I}_2\), 满足

\[\mathcal{I}_1 \cap \mathcal{I}_2 = \empty, \]

假设 \(\mathcal{MP}\) 是一个量化曝光率的指标, 则产品侧的 fairness 定义为:

\[\tag{1} \text{DPF}(A, \mathcal{I}_1, \mathcal{I}_2) := \mathbb{E}[\mathcal{MP}(i, A)| i \in \mathcal{I}_1] - \mathbb{E}[\mathcal{MP}(i, A)| i \in \mathcal{I}_2]. \]

自然 \(\text{DPF} \rightarrow 0\) 是一个理想的结果.

注: 作者将交互次数 top 20% 的产品定义为 popular 的产品 (short-head items), 而剩下的为 long-tail items.
注: \(\mathcal{MP}\) 可以用比如曝光次数的统计.

用户侧的 fairness

根据用户的活跃程度, 可以分为: frequent users \(\mathcal{U}_1\), less-frequent users \(\mathcal{U}_2\), 同样满足

\[\mathcal{U}_1 \cap \mathcal{U}_2 = \empty. \]

假设 \(\mathcal{MC}\) 是一个能够衡量推荐相关性的一个指标 (比如 NDCG, \(F_1\) score, Recall), 理想的推荐系统, 应该对于无论是活跃的用户还是不怎么活跃的用户给出近似质量的推荐结果, 即希望

\[\text{DCF} (A, \mathcal{U}_1, \mathcal{U}_2) =\mathbb{E} [\mathcal{MC} (u, A)|u \in \mathcal{U}_1] -\mathbb{E} [\mathcal{MC} (u, A)|u \in \mathcal{U}_2] \]

趋于 \(0\).

注: 活跃用户和非活跃用户的区分, 本文在做实验的时候, 选择交易次数在 top 5% 的用户为活跃用户, 剩下的为非活跃用户.
注: 本文采用的是 NDCG.

两侧的 fairness

为了兼顾二者, 作者定义 Cunsumer-Producer fairness evaluaction (mCPF):

\[\text{mCPF} (w) = w \cdot \text{DPF} + (1 - w) \cdot \text{DCF}, \]

其中 \(w\) 反映了对于哪种 fairness 的一个倾向.

主要内容

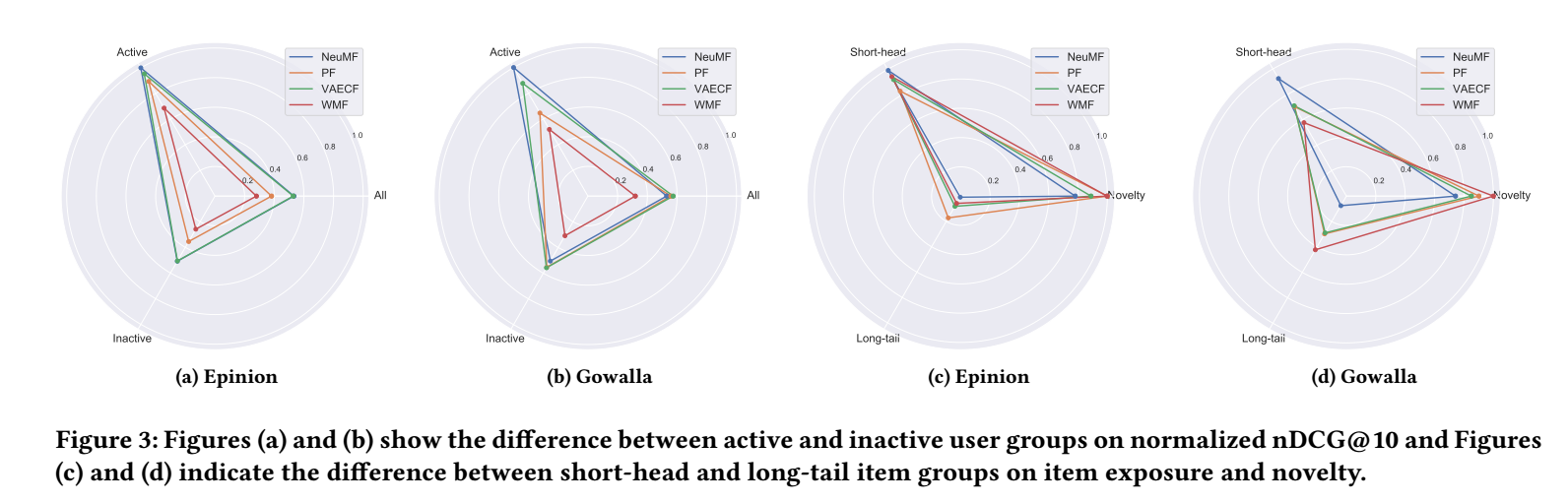
从上图可以看到, 大部分的算法都是偏向活跃用户和头部产品 (虽然从做生意的角度好像怎么做没啥问题). 但是的确对其它用户和产品有些不公平.

于是本文就提出了一个 re-ranking post-hoc 算法, 其解决:

\[\begin{array}{rc} \max_{A_{ui}} & \sum_{u \in \mathcal{U}} \sum_{i = 1}^N \mathcal{S}_{ui} A_{ui} - \lambda_1 \cdot \text{DCF}(A, \mathcal{U}_1, \mathcal{U}_2) - \lambda_2 \cdot \text{DPF}(A, \mathcal{I}_1, \mathcal{I}_2) \\ \text{s.t.} & \sum_{i=1}^N A_{ui} = K, A_{ui} \in \{0, 1\} \end{array} \]

其中 \(\lambda_1, \lambda_2\) 反映对哪个 fairness 重视程度的一个超参数, 比如如果我们令 \(\lambda_2 = 0\), 而为 \(\lambda_1\) 设置一个较大的数, 那么就变成了倾向用户公平性的一个算法.

作者提出了两种求解算法, 一种是将 \(A_{ui} \in \{0, 1\}\) 的条件放缩为 \(0 \le A_{ui} \le 1\), 然后用线性规划求解, 另一种是转换为 背包问题 ? 说实话, 我没 get 到算法 2 和背包问题的联系.

看下来, 感觉 fairness 的领域对于指标的设计, 问题的研究还比较初级.