Causal Representation Learning for Out-of-Distribution Recommendation

概
符号说明
主要内容
代码

Wang W., Lin X., Feng F., He X., Lin M. and Chua T. Causal representation learning for out-of-distribution recommendation. In International World Wide Web Conferences (WWW), 2022.

概

现阶段, 大部分的推荐系统都是在历史交互信息的基础进行预测的, 但是这种方式建立在历史数据和未来的交互处于独立同分布的假设下才有效. 否则很可能会面临严重的 Out-of-Distribution (OOD) 问题. 设想, 一个人的年龄和收入会影响他买东西的价格, 品牌, 类型等, 但同时这些也受一些未知因素影响, 比如:

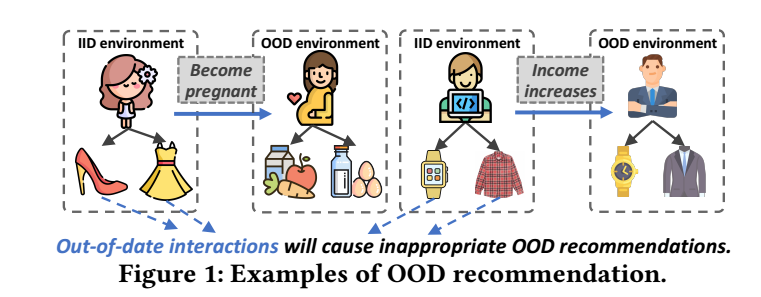
本文就主要是通过因果模型来解决这一问题.

符号说明

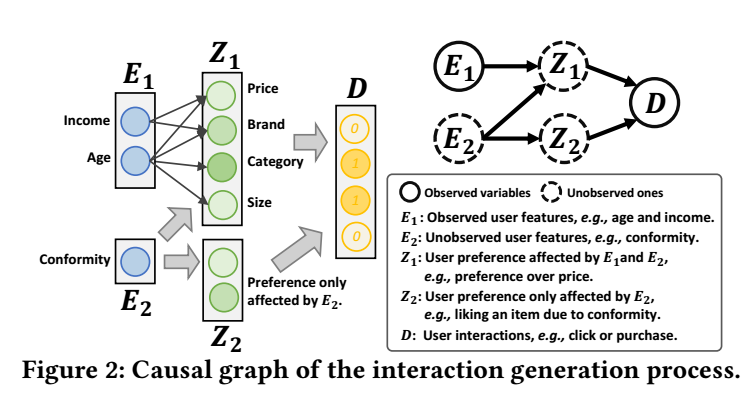
$\bm{e}_1 \in E_1$ , 观测到的用户特征;
$\bm{e}_2 \in E_2$ , 未观测到的用户特征;
$\bm{z}_1 \in Z_1$ , 用户的倾向;
$\bm{z}_2 \in Z_2$ , 仅仅由 $E_2$ 所决定的偏好;
$\bm{d} \in D$ , 用户交互, 比如是否点击, 购买等;
$I$ , items 的数量.

主要内容

构建模型

作者认为这些因素的模型如 Figure 所示, 为此, 作者用 VAE 构建这样的一个模型.

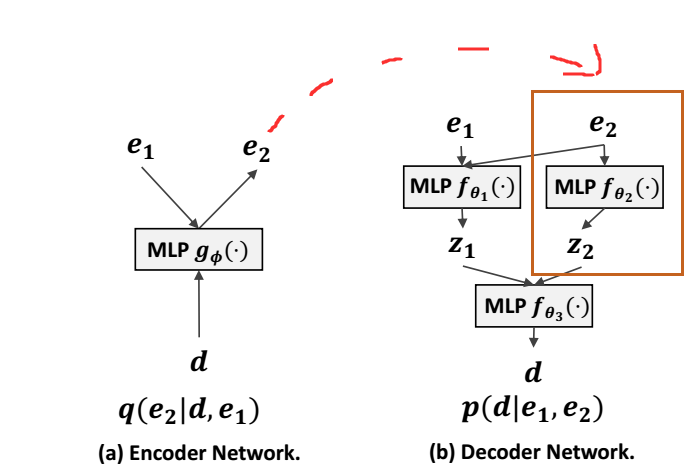
Encoder
1. 用户特征 $\bm{e}_1$ 和历史交互信息 $\bm{d}$ 得到
  $\bm{\mu}_{\phi}, \bm{\sigma}_{\phi} = g_{\phi}(\bm{e}_1, \bm{d});$
2. 假设 $\bm{e}_2$ 服从先验分布 $\mathcal{N}(0, I_k)$ , 拟合的分布为:
  $\tag{E-1} q_{\phi}(\bm{e}_2|\bm{d}, \bm{e}_1) := \mathcal{N}(\bm{e}_2; \bm{\mu}_{\phi} (\bm{d}, \bm{e}_1), \mathrm{diag}\{\bm{\sigma}_{\phi}^2(\bm{d}, \bm{e}_1\});$
3. 从拟合的分布 $q_{\phi}$ 从采样得到 $\bm{e}_2$ .
Decoder
1. 通过 MLP $f_{\theta_1}, f_{\theta_2}$ 分别得到:
  $\bm{\mu}_{\theta_1}, \bm{\sigma}^2_{\theta_1} = f_{\theta_1}(\bm{e}_1, \bm{e}_2), \\ \bm{\mu}_{\theta_2}, \bm{\sigma}^2_{\theta_2} = f_{\theta_2}(\bm{e}_2); \\$
2. 假设 $\bm{z}_1, \bm{z}_2$ 分别服从
  $\tag{D-1} \bm{z}_1 \sim \mathcal{N}(\bm{\mu}_{\theta_1}, \mathrm{diag}(\bm{\sigma}_{\theta_1}^2)); \\ \bm{z}_2 \sim \mathcal{N}(\bm{\mu}_{\theta_2}, \mathrm{diag}(\bm{\sigma}_{\theta_2}^2)); \\$
3. 给定 $\bm{z}_1, \bm{z}_2$ , MLP $f_{\theta_3}$ 输出 logits $f_{\theta_3} (\bm{z}_1, \bm{z}_2) \in \mathbb{R}^{I}$ , 经由 softmax $\pi(\cdot)$ 得到概率向量
  $\pi(f_{\theta_3} (\bm{z}_1, \bm{z}_2)) \in \mathbb{R}^{I}, \: \sum_{i=1}^I \pi_i = 1;$
4. 假设 $\bm{\hat{d}}$ 服从多项分布:
  $\tag{D-2} \bm{\hat{d}} \sim \text{Mult} (N, \pi(f_{\theta_3}(\bm{z}_1, \bm{z}_2))),$
  其中 $N$ 是该用户交互的次数.

训练

首先, 注意到我们只有 $\bm{e}_1$ , 历史交互信息 $\bm{d}$ 和 target $\bm{\hat{d}}$ 是观测到的, 故可以通过极大似然估计来优化:

\log p (\hat{d} | e_{1}) = \log \int p (\hat{d}, e_{2} | e_{1}) d e_{2} = \log \int p (\hat{d} | e_{1}, e_{2}) p (e_{2}) d e_{2},

$\log p(\bm{\hat{d}}|\bm{e}_1) =\log \int p(\bm{\hat{d}}, \bm{e}_2 | \bm{e}_1) d \bm{e}_2 =\log \int p(\bm{\hat{d}} | \bm{e}_1, \bm{e}_2) p(\bm{e}_2) d \bm{e}_2,$

注意, 上面的 $\bm{e}_2$ 是服从 $\mathcal{N}(0, I_k)$ 的, 独立于 $\bm{e}_1$ .

和普通的 VAE 一样, 因为并没有观测到 $\bm{e}_2$ , 故只能采取最大化 ELBO 的做法, 即:

max_{ϕ, Θ} E_{q_{ϕ} (e_{2} | \cdot)} [\log p_{Θ} (\hat{d} | e_{1}, e_{2}))] - KL (q_{ϕ} (e_{2} | \cdot) ‖ p (e_{2})) .

$\max_{\phi, \Theta} \quad \mathbb{E}_{q_{\phi}(\bm{e_2}|\cdot)} [\log p_{\Theta}(\bm{\hat{d}}| \bm{e}_1, \bm{e}_2))] - \text{KL} (q_{\phi}(\bm{e}_2| \cdot) \| p(\bm{e}_2)).$

因为 (E-1) 的缘故, 对于第二项我们可以直接求解;
对于前者, 可以展开得到:
$p(\bm{\hat{d}}|\bm{e}_1, \bm{e}_2) = \int \int p_{\theta_1}(\bm{z}_1 | \bm{e}_1, \bm{e}_2) p_{\theta_2}(\bm{z}_2| \bm{e}_2) p_{\theta_3}(\bm{\hat{d}} | \bm{z}_1, \bm{z}_2) d \bm{z}_1 d \bm{z}_2,$
可以通过 MCMC 采样逼近 (重参数化):
$p(\bm{\hat{d}}| \bm{e}_1, \bm{e}_2) \approx \frac{1}{LM} \sum_{a=1}^L \sum_{b=1}^M p(\bm{\hat{d}}|\bm{z}_1^a, \bm{z}_2^b), \: \bm{z}_1^a \sim p(\bm{z}_1|\bm{e}_1 \bm{e}_2) \: \bm{z}_2^b \sim p(\bm{z}_2|\bm{e}_2);$
但是这样子还是比较费时, 因为必须得重复 LM 次前向传播, 故实际上使用的是:
$p(\hat{d}|\bm{e}_1, \bm{e}_2) \approx p(\bm{\hat{d}}| \bm{\bar{z}}_1, \bm{\bar{z}}_2), \: \bm{\bar{z}}_1 = \frac{1}{L} \sum_{a=1}^L \bm{z}_1^a, \: \bm{\bar{z}}_2 = \frac{1}{M} \sum_{b=1}^M \bm{z}_2^b.$
Q: 为什么不干脆设 $Z_1 \sim \delta (Z - f_{\theta_1}(E_1, E_2)), Z_2 \sim \delta (Z - f_{\theta_2}(E_2))$ ?
最后
$\log p(\bm{\hat{d}}|\bm{\bar{z}}_1, \bm{\bar{z}}_2) = \frac{i=1}{I} d_i \log \pi_i (f_{\theta_3} (\bm{\bar{z}}_1, \bm{\bar{z}}_2)).$

注: 对于损失, 采用了以加权的版本:

max_{ϕ, Θ} E_{q_{ϕ} (e_{2} | d, e_{1})} [\log p_{Θ} (\hat{d} | e_{1}, e_{2}))] - β \cdot KL (q_{ϕ} (e_{2} | d, e_{1}) ‖ p (e_{2})) .

$\max_{\phi, \Theta} \quad \mathbb{E}_{q_{\phi}(\bm{e_2}|\bm{d}, \bm{e}_1)} [\log p_{\Theta}(\bm{\hat{d}}| \bm{e}_1, \bm{e}_2))] - \beta \cdot \text{KL} (q_{\phi}(\bm{e}_2| \bm{d}, \bm{e}_1) \| p(\bm{e}_2)).$

推断

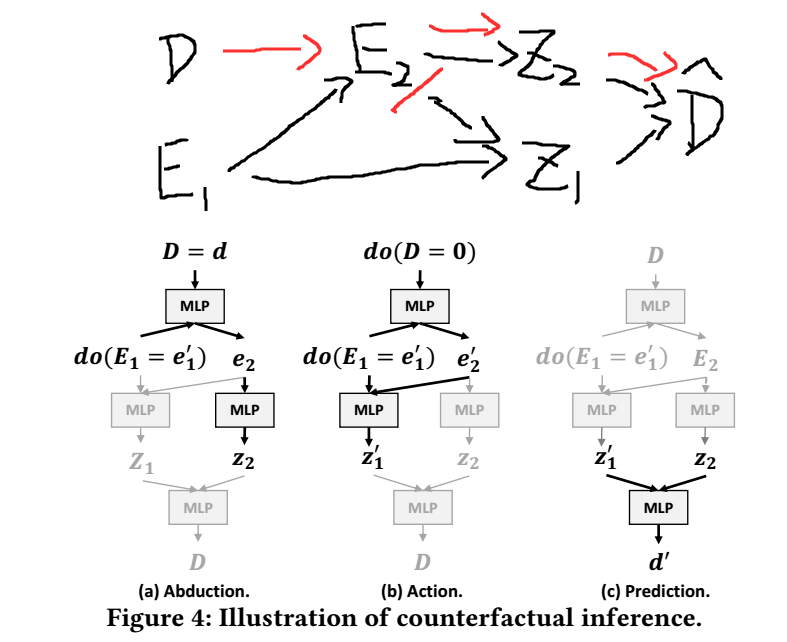
因为 $\bm{e}_2$ 的采样和历史信息 $\bm{d}$ 有关, 但是呢, 这也有可能导致将历史的过时的交互信息传递给下游的 $\bm{z}_1$ , 因此, 为了切断这个联系, 作者采用 $do(D=0)$ 的方式 (见图4 (b)) 生成 $\bm{z}_1$ , 而采用 $do(D = \bm{d})$ 的方式生成 $\bm{z}_2$ , 保留历史信息对于 $Z_2$ 的推断. 最后结合二者用于预测 $\bm{d}'$ ( $\bm{\hat{d}}$ ).