Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Networks
概
FM 的二阶部分可以看成
\[\bm{1}^T \sum_{j > i} (\bm{v}_i \odot \bm{v}_j) x_i x_j,
\]
故实际上是
\[\{ x_i x_j (\bm{v}_i \odot \bm{v}_j)\}
\]
的一个平均池化. 但是在实际中, 交叉特征也是有区别的, 一种更加合适的方法应该是加权平均,
\[\bm{1}^T \sum_{j > i} a_{ij} (\bm{v}_i \odot \bm{v}_j) x_i x_j,
\]
这里 \(a_{ij}\) 代表所对应的交叉权重的比重. 本文, 作者通过注意力机制来建模.
主要内容
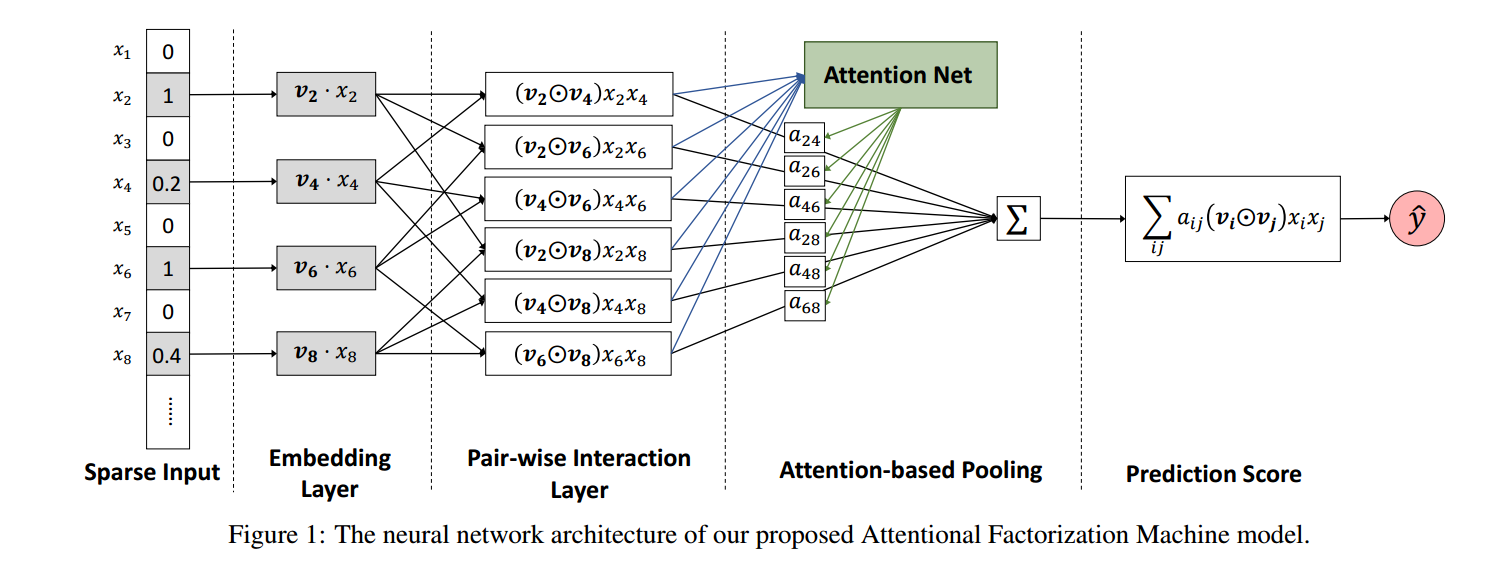
- 稀疏特征 \(\bm{x}\), 定义 \(\mathcal{R}_x = \{(i, j): j > i, x_i \not = 0, x_j \not = 0\}\)
- embedding layer:
\[\xi = \{x_i \bm{v}_i\};
\]
- Pair-wise interaction layer:
\[f_{PI}(\xi) = \{(\bm{v}_i \odot \bm{v}_j ) x_i x_j \}_{\mathcal{R}_x};
\]
- Attention-based Pooling layer:
\[f_{Att}(f_{PI}(\xi)) = \sum_{(i, j) \in \mathcal{R}_x} a_{ij} (\bm{v}_i \odot \bm{v}_j) x_i x_j;
\]
- 预测
\[\hat{y}_{AFM}(\bm{x}) = w_0 + \bm{w}^T \bm{x} + \bm{p}^T \sum_{(i, j) \in \mathcal{R}_x} a_{ij} (\bm{v}_i \odot \bm{v}_j) x_i x_j.
\]
- 训练
\[L_r = \sum_{\bm{x}} (\hat{y}_{AFM}(\bm{x}) - y(\bm{x}))^2.
\]
诚然, 我们可以直接训练权重 \(a_{ij}\), 但是训练集中很难囊括所有的交叉特征,这意味部分 \(a_{ij}\) 可能压根没有进行训练过! 故作者通过 attentin network 建模.
Attention network
\[a_{ij}' = \bm{h}^T \text{ReLU}(W (\bm{v}_i \odot \bm{v}_j) x_i x_j + \bm{b}), \\
a_{ij} = \frac{\exp (a_{ij}')}{\sum_{(i, j) \in \mathcal{R}_x} \exp (a_{ij}')}.
\]
细节
- L2 正则化;
- DropOut;
- \(\bm{v} \in \mathbb{R}^{256}\);
- \(\bm{h} \in \mathbb{R}^{256}\).
代码
[official]
[PyTorch]
[TensorFlow]


