Statistical Comparisons of Classifiers over Multiple Data Sets

目录

[1] Dem\check{s}ar, J. Statistical comparisons of classifiers over multiple data sets. Journal of Machine Learning Research (JMLR). vol. 7, pp. 1-30, 2006.

[2] Benavoli A., Corani G., Dem\check{s}ar J. and Zaffalon M. Time for a change: a tutorial for comparing multiple classifiers through bayesian analysis. Journal of Machine Learning Research (JMLR). vol. 18, pp. 2653-2688, 2017.

对假设检验这块不是很懂, 下面的整理难免有纰漏.

双算法 vs 单数据集

Frequentist correlated t-test

  1. 算法A, B独立地在k折数据集上跑\(n\)次, 收集评估指标 (比如正确率, 召回率等) \(a_1, a_2, \cdots, a_n\) 和 \(b_1, b_2, \cdots, b_n\);
  2. 记k折数据集的数据集大小为 \(N = N_{train} + N_{test}\);
  3. 计算二者的差 \(x_1, x_2, \cdots, x_n, \: x_i = a_i - b_i\);
  4. 计算

\[\bar{x} = \frac{1}{n} \sum_{i=1}^n x_i, \\ \hat{\sigma} = \sqrt{\frac{1}{n-1}\sum_{i=1}^n (x_i - \bar{x})^2}; \]

  1. 计算统计量

\[\tag{1} t(\bm{x}, \mu) = \frac{\bar{x} - u}{\sqrt{\hat{\sigma}^2(\frac{1}{n} + \frac{\rho}{1 - \rho})}}, \]

其中 \(\rho = \frac{N_{test}}{N}\) (一般的 t-test 取\(\rho=0\), 但是因为k折的缘故, 每个实验之间不是完全独立的, 所以需要 correlated t-test).
5. (1) 中的 \(t\) 服从 n-1 个自由度的学生氏分布, 给出如下的假设检验:

\[H_0: \mu = 0; H_1: \mu \not = 0, \]

即若原假设成立, 我们就认为两个算法是相近的.
7. 因为学生氏分布是关于0对称的, 故我们通常选择双侧的假设检验, \(t(\bm{x}, \mu)\) 的 p-value 为

\[p = 2 \cdot (1 - \mathcal{T}_{n-1}(|t(\bm{x}, 0)|)), \]

其中 \(\mathcal{T}_{n-1}(\cdot)\) 表示 n-1 个自由度的学生氏分布的分布函数.
8. 通常选定一个阈值, 比如 0.05, 当

\[p < 0.05 \]

时拒绝 \(H_0\), 此时算法 A, B 在该数据集上有明显区别.

注: \(n\) 次数最好足够大, 比如 \(> 30\).

双算法 vs 多数据集

数据举例

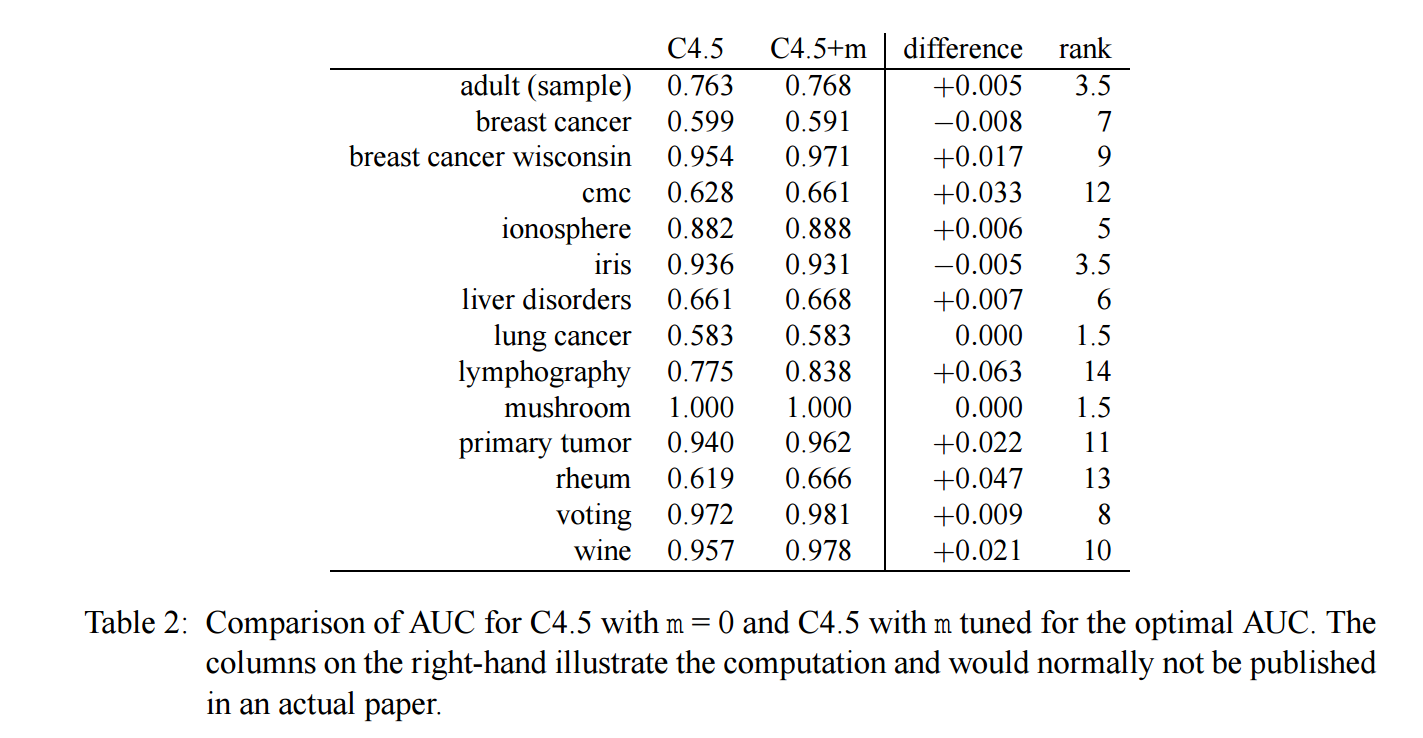
表格中每一行为:
[数据集 \(i\) ] [算法C4.5的评估 \(a_i\)] [算法C4.5+m的评估 \(b_i\)] [\(d_i = a_i - b_i\)] [\(\text{rank}(d_i) = \text{rank}(|d_i|)\)].

注: 给 difference 排序是根据绝对值来排序的, 此外评估 \(a_i, b_i\) 一般来说是多次重复实验的平均值.
注: 出现奇数的原因是, 比如 \(0\) 来说, 应该是 \(1, 2\), 取平均值 \(1.5\).

Wilcoxon signed-ranks test

  1. 计算

\[R^+ = \sum_{d_i > 0} \text{rank}(d_i) + \frac{1}{2}\text{rank}(d_i), \\ R^- = \sum_{d_i < 0} \text{rank}(d_i) + \frac{1}{2}\text{rank}(d_i). \]

  1. 当数据集数目 \(N\) 比较少的时候, 计算统计量

\[T = \min (R^+, R^-). \]

它的 critical value 可通过下方查表可得.
3. 当数据集数目 \(N\) 足够多的时候, 可以计算统计量

\[z = \frac{T - \frac{1}{4} N (N + 1)}{\sqrt{\frac{1}{24}N (N + 1) (2N + 1)}}, \]

且\(z\) 近似服从标准正态分布 \(\mathcal{N}(0, 1)\).
4. 建立假设检验:

\[H_0: \text{算法A, B一致}; H_1: \text{算法A, B显著不同}. \]

对于情况2., 当T过小的时候我们要拒绝原假设, 对于情况3, 当 \(z\) 过小或者过大的时候我们应该拒绝原假设.

注: [Wilcoxon_signed-rank_test-wiki].
注: 个人认为, 下表的值其实是 \(R^+\)或者\(R^-\)的 critical value, 而非 \(T\), 注意到:

\[R^+ + R^- = \frac{N(N+1)}{2}. \]

此时 \(R^+\) 或 \(R^-\)在\(H_0\)假设下大致服从如下的分布(应该离散化):

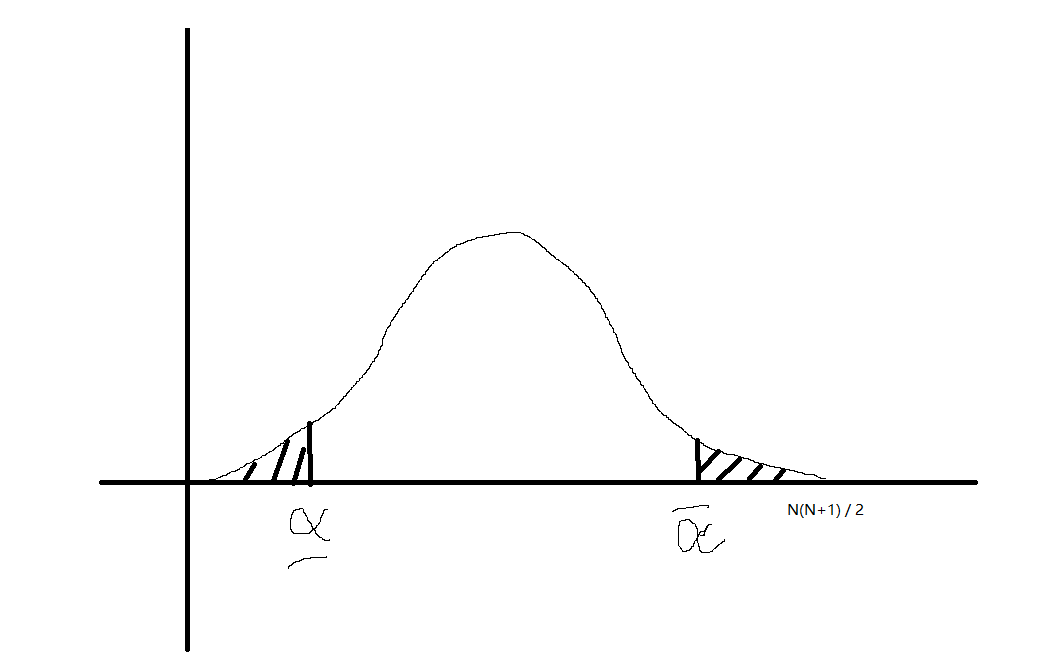
此时 \(R^+ < \underline{\alpha}\) 或 \(R^+ > \overline{\alpha}\) 时应该拒绝原假设, 而后者又等价于 \(R^{-} < \underline{\alpha}\), 故我们只需考虑

\[T = \min(R^+, R^-) \]

是否小于 \(\underline{\alpha}\) 即可.

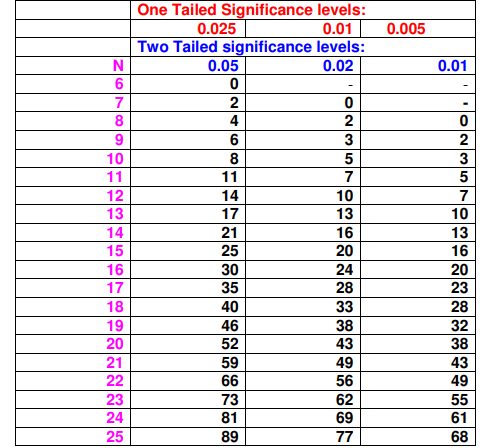
例子

还是以最上方的14个数据集为例, 可得

\[R^+ = 3.5 + 9 + 12 + 5 + 6 + 14 + 11 + 13 + 8 + 10 + 1.5 = 93 \\ R^- = 7 + 3.5 + 1.5 = 12, \]

查表可知 \(N=14\) 时, 有 \(p < 0.01 < 0.05\), 故拒绝原假设, 认为两种算法是显著不同的.

scipy-wilcoxon


# %%
import numpy as np
import pandas as pd
from scipy.stats import wilcoxon


# %%
data = [
    ["adult(sample)", 0.763, 0.768, 0.005, 3.5],
    ["breast cancer", 0.599, 0.591, -0.008, 7],
    ["breast cancer wisconsin", 0.954, 0.971, 0.017, 9],
    ["cmc", 0.628, 0.661, 0.033, 12],
    ["ionosphere", 0.882, 0.888, 0.006, 5],
    ["iris", 0.936, 0.931, -0.005, 3.5],
    ["liver disorders", 0.661, 0.668, 0.007, 6],
    ["lung cancer", 0.583, 0.583, 0.000, 1.5],
    ["lymphography", 0.775, 0.838, 0.063, 14],
    ["mushroom", 1.000, 1.000, 0.000, 1.5],
    ["primary tumor", 0.940, 0.962, 0.022, 11],
    ["rheum", 0.619, 0.666, 0.047, 13],
    ["voting", 0.972, 0.981, 0.009, 8],
    ["wine", 0.957, 0.978, 0.021, 10]
]

data = pd.DataFrame(data, columns=["dataset", "A", "B", "diff", "rank"])


# %%
wilcoxon(x=data['A'], y=data['B'], zero_method='zsplit') # or x = data['diff]
# Out: WilcoxonResult(statistic=12.0, pvalue=0.01096849656422473)

注: scipy 中的 wilcoxon 默认采用的是 zero_method = 'wilcox', 它会把 \(d_i=0\) 的部分舍去, 想要和论文 [1] 一致, 请使用 zero_method = 'zsplit'.

多算法 vs 多数据集

假设共有 \(K\) 个算法:

\[\mathcal{A}_1, \mathcal{A}_2, \cdots, \mathcal{A}_K, \]

并假设每个算法在数据集 \(\mathcal{D}_j, j=1,2,\cdots, N\) 上的评估(类似地, 通常为多次重复实验的平均):

\[a_{ij}. \]

下面给出是检验流程可以归结如下:

  1. 首先通过一个统计量判断这些算法间是否有显著差异;
  2. 如果有, 则进行 pos-hoc 测试, 即对这些算法进行 pairwise 的比较, 看是哪些和哪些算法有差异.

ANOVA

ANOVA 的假设检验为:

\[H_0: \mu_1 = \mu_2 = \cdots = \mu_K, \]

我们可以令

\[S_T = \sum_{i=1}^K\sum_{j=1}^N (a_{ij} - \bar{a}) = S_E + S_G \]

为总偏差, 其中 组内误差 \(S_E\) 和 组间误差 \(S_G\) 为

\[S_E = \sum_{i=1}^K \sum_{j=1}^N (a_{ij} - \bar{a}_i)^2, \\ S_G = \sum_{i=1}^K \sum_{j=1}^N (\bar{a}_i - \bar{a})^2. \]

其中 \(\bar{a}_i = \frac{1}{N}\sum_j a_{ij}\), \(\bar{a} = \frac{1}{NK} \sum_i \sum_j a_{ij}\).
可以得到统计量

\[z = \frac{S_G / (K - 1)}{S_E / K(N-1)}, \]

当\(H_0\)成立的时候服从 \(F(K - 1, K(N-1))\).

ANOVA 例子


from scipy.stats import f_oneway

# %%
A = [24.5, 23.5, 26.4, 27.1, 29.9]
B = [28.4, 34.2, 29.5, 32.2, 30.1]
C = [26.1, 28.3, 24.3, 26.2, 27.8]
# %%
f_oneway(A, B, C)
# Out: F_onewayResult(statistic=7.137827822120864, pvalue=0.009073317468563076)

说明这几个之间是显著的 \(p < 0.05\).

Tukey test

通过上述的 ANOVA 可以得到算法间是否相似的结论, 但倘若拒绝了 \(H_0\), 接下来应该讨论哪些和哪些是有显著区别的, 可以通过 Tukey test 来进行测试.

也称为: Tukey's test, Tukey method, Tukey's honest significance test, or Tukey's HSD

[wiki-Tukey test]

Tukey test 为两两算法 \(\mathcal{A}_i, \mathcal{A}_j\) 的相近程度做检验.

其流程如下:

  1. 计算二者的均值 \(\bar{a}_i, \bar{a}_j\);
  2. 计算统计量:

\[z = \frac{|\bar{a}_i - \bar{a}_j|}{\sqrt{S / N}}; \]

这里的分母部分为标准误 (standard error), 其中

\[S = \frac{SE}{K(N-1)}, \]

服从 \((K, K(N - 1))\) 的 Studentized range 分布.
3. 使用单侧的假设检验, 记 critical value 为 \(q\), 则若

\[z > q \]

则拒绝原假设

\[H_0: \mu_i = \mu_j, \]

即此时 \(\mathcal{A}_i, \mathcal{A}_j\) 有显著不同.

scipy-tukey_hsd
statsmodels-tukeyhsd

from statsmodels.stats.multicomp import pairwise_tukeyhsd
# scipy 1.8.0 也有了 tukey_hsd 方法;
# Python >= 3.8
# %%
A = [24.5, 23.5, 26.4, 27.1, 29.9]
B = [28.4, 34.2, 29.5, 32.2, 30.1]
C = [26.1, 28.3, 24.3, 26.2, 27.8]
scores = A + B + C
groups = ['A'] * len(A) + ['B'] * len(B) + ['C'] * len(C)
# %%
res = pairwise_tukeyhsd(
    endog=scores, groups=groups, alpha=0.05
)
print(res)
# Out:
# Multiple Comparison of Means - Tukey HSD, FWER=0.05 
# ====================================================
# group1 group2 meandiff p-adj   lower   upper  reject
# ----------------------------------------------------
#      A      B      4.6 0.0144  0.9526  8.2474   True
#      A      C     0.26    0.9 -3.3874  3.9074  False
#      B      C    -4.34 0.0203 -7.9874 -0.6926   True
# ----------------------------------------------------

注: 其中的 meandiff 为: \(\bar{a}_i - \bar{a}_j\), 而非上述的 \(z\).

Friedman test

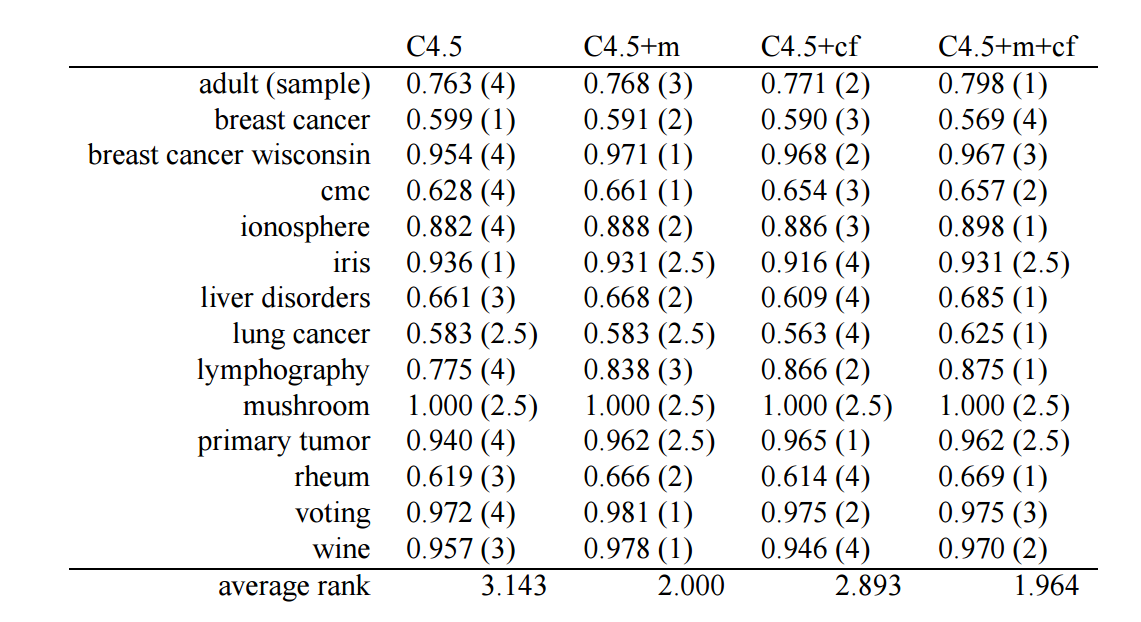
注: voting 一行的排序有误, 应该为

\[4, 1, 2.5, 2.5. \]

注: 和 Wilcoxon signed-ranks test 不同, 越大的指标排名越靠前 (因为这表示越好).

wiki-Friedman_test

  1. 根据 \(a_{ij}, i=1,2,\cdots, K, j = 1,2,\cdots, N\), 对每一个数据集 \(j\) 进行排序, 得到

\[r_{ij}, i=1,2,\cdots, K, j=1,2,\cdots, N, \]

表示算法 \(\mathcal{A}_i\) 在数据集 \(\mathcal{D}_j\) 上的序.
2. 计算算法 \(\mathcal{A}_i\) 在不同数据集上的平均排序

\[R_i = \frac{1}{N} \sum_{j = 1}^N r_{ij}. \]

  1. 定义 Friedman 统计量

\[\chi_F^2 = \frac{12 N}{k (k+1)} [\sum_i R_i^2 - \frac{k(k+1)^2}{4}], \]

当 \(N, K\) 足够大 (比如 \(N > 10, K > 4\)) 的时候该统计量服从 \(K - 1\) 个自由度的卡方分布, 否则需要通过查表 (特殊设计的) 来做检验.
4. 或者采用如下调整过的统计量

\[F_F = \frac{(N - 1)\chi_F^2}{N(k-1) - \chi_F^2}, \]

其服从 \(K - 1\), \((K - 1)(N-1)\) 个自由度的 F 分布.

下表是关于 \(\chi_F^2\) 的 Upper critical values.

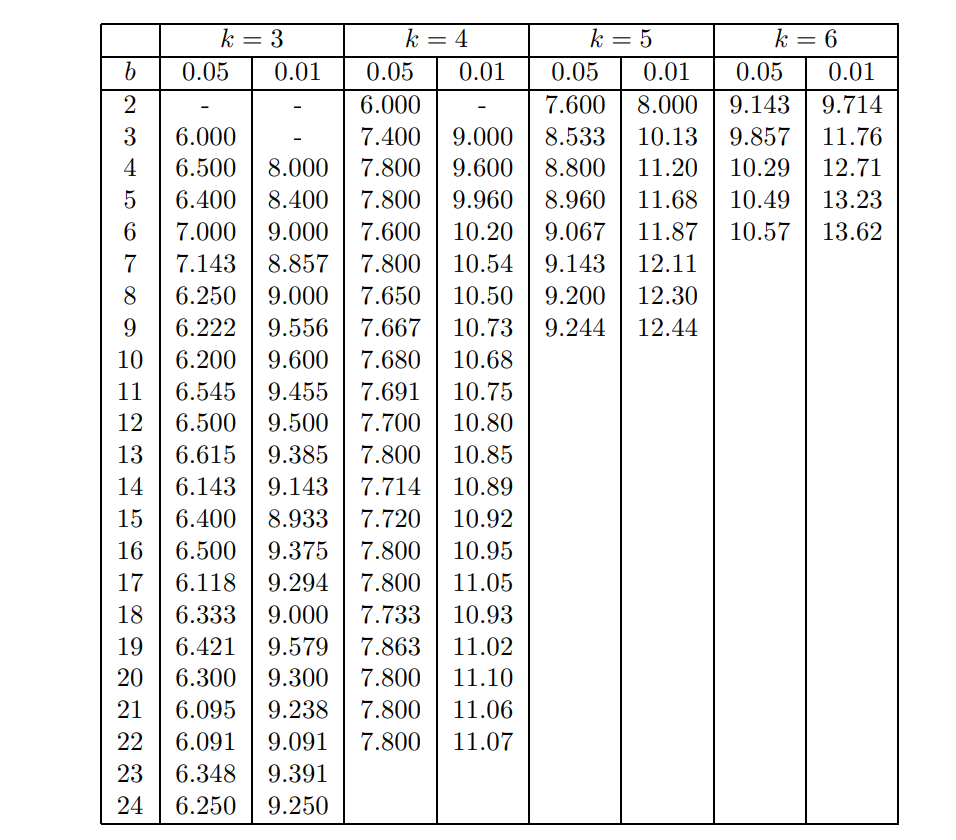
例子

scipy-fridmanchisquare

注: scipy 中的和 [1] 中的有点不同.

# %%
data = [
    [0.763, 0.768, 0.771, 0.798],
    [0.599, 0.591, 0.590, 0.569],
    [0.954, 0.971, 0.968, 0.967],
    [0.628, 0.661, 0.654, 0.657],
    [0.882, 0.888, 0.886, 0.898],
    [0.936, 0.931, 0.916, 0.931],
    [0.661, 0.668, 0.609, 0.685],
    [0.583, 0.583, 0.563, 0.625],
    [0.775, 0.838, 0.866, 0.875],
    [1.000, 1.000, 1.000, 1.000],
    [0.940, 0.962, 0.965, 0.962],
    [0.619, 0.666, 0.614, 0.669],
    [0.972, 0.981, 0.975, 0.975],
    [0.957, 0.978, 0.946, 0.970]
]
data = np.array(data)
# %%
from scipy.stats import friedmanchisquare
res = friedmanchisquare(data[:, 0], data[:, 1], data[:, 2], data[:, 3])
res
# Out: FriedmanchisquareResult(statistic=10.952380952380956, pvalue=0.011986176325417788)
# %%
from scipy.stats import rankdata, chi2, f
def friedman_test(*groups, corrected: bool = False):
    """
    groups: A, B, C, array-like
    corrected:
        False: normal, Chi2
        True: F-distribution
    """
    data = np.stack(groups, axis=1)
    N, K = data.shape
    rank = np.apply_along_axis(rankdata, 1, -data)
    mrank = np.mean(rank, axis=0, keepdims=True)
    statistic = (12 * N) * (np.sum(mrank ** 2) - K * (K + 1) ** 2 / 4) / (K * (K + 1))
    if corrected:
        statistic = (N - 1) * statistic / (N * (K - 1) - statistic)
        p_values = 1 - f.cdf(statistic, K - 1, (N - 1) * (K - 1))
    else:
        p_values = 1 - chi2.cdf(statistic, K - 1)
    return statistic, p_values

# %%
friedman_test(data[:, 0], data[:, 1], data[:, 2], data[:, 3])
# Out: (9.857142857142824, 0.019820334037905174)

# %%
friedman_test(data[:, 0], data[:, 1], data[:, 2], data[:, 3], corrected=True)
# Out: (3.9866666666666495, 0.01435244621602394)

可见无论是否用修正的, 结果(单侧) $ p < 0.05$, 故我们拒绝原假设, 认为这四个算法有显著的区别.
细心的读者可能会发现, 我们实现的函数算出来的结果和原文中有出入, 这是因为文中给出的 voting 数据集的排序是有误的.

Nemenyi test

注: 这部分背后的逻辑不是很明白啊.

  1. 计算统计量

\[z = (R_i - R_j) / \sqrt{\frac{K(K+1)}{6N}}. \]

  1. 通过查表得知 critical values, 或者通过 Studentized range distribution 得到 \(\hat{q}_{\alpha}\), 而我们所需的为

\[q_{\alpha} = \frac{\hat{q}_{\alpha}}{\sqrt{2}} \]

注: 分母部分其实也是 standard error, 只不过这个不是估计出来的而是计算的出来的, 不过我计算出来的结果是:

\[\sqrt{\frac{(K - 1)(K+1)}{6N}}, \]

不晓得哪里出错了.

import scikit_posthocs as sp
# pip install scikit-posthocs
data = pd.DataFrame(data, columns=['A', 'B', 'C', 'D'])
sp.posthoc_nemenyi_friedman(data)
# Out: P-values
# 	    A	        B	        C	    D
# A	1.000000	0.088552	0.90000	0.061744
# B	0.088552	1.000000	0.22683	0.900000
# C	0.900000	0.226830	1.00000	0.170230
# D	0.061744	0.900000	0.17023	1.000000

从上面的结果可以看出, Nemenyi test 在此情况下不是很给力, pairwise 的结果 \(p > 0.05\), 无法抓住两两间的差异性, 这与 Friedman test 的结果有出入.

Dunn test

形式和上方的 Nemenyi test 是一致的, 只是加入了对不同的 p-value 的调整.

Bonferroni-Dunn test
import numpy as np

# %%
data = [
    [0.763, 0.768, 0.771, 0.798],
    [0.599, 0.591, 0.590, 0.569],
    [0.954, 0.971, 0.968, 0.967],
    [0.628, 0.661, 0.654, 0.657],
    [0.882, 0.888, 0.886, 0.898],
    [0.936, 0.931, 0.916, 0.931],
    [0.661, 0.668, 0.609, 0.685],
    [0.583, 0.583, 0.563, 0.625],
    [0.775, 0.838, 0.866, 0.875],
    [1.000, 1.000, 1.000, 1.000],
    [0.940, 0.962, 0.965, 0.962],
    [0.619, 0.666, 0.614, 0.669],
    [0.972, 0.981, 0.975, 0.975],
    [0.957, 0.978, 0.946, 0.970]
]
data = np.array(data)


# %%
import scikit_posthocs as sp
sp.posthoc_dunn(data.T, p_adjust='bonferroni')
# Out:
#   1	2	3	4
# 1	1.0	1.0	1.0	1.0
# 2	1.0	1.0	1.0	1.0
# 3	1.0	1.0	1.0	1.0
# 4	1.0	1.0	1.0	1.0

很奇怪的结果.

Holm’s step-down
# %%
import scikit_posthocs as sp

sp.posthoc_dunn(data.T, p_adjust='holm')
# Out:
#   1	2	3	4
# 1	1.0	1.0	1.0	1.0
# 2	1.0	1.0	1.0	1.0
# 3	1.0	1.0	1.0	1.0
# 4	1.0	1.0	1.0	1.0
Hochberg’s step-up
# %%
import scikit_posthocs as sp
sp.posthoc_dunn(data.T, p_adjust='simes-hochberg')
# Out:
#   1	        2	        3	        4
# 1	1.000000	0.986129	0.986129	0.986129
# 2	0.986129	1.000000	0.986129	0.986129
# 3	0.986129	0.986129	1.000000	0.986129
# 4	0.986129	0.986129	0.986129	1.000000

Conover* test

Conover test 文中并没有提及, 但是这个感觉挺有用的, 能够准确分别出, 得出的结论和文中的也一样.


# %%
import scikit_posthocs as sp
sp.posthoc_conover_friedman(data)
# Out:
# 	0	        1	        2	        3
# 0	1.000000	0.018734	0.648091	0.012889
# 1	0.018734	1.000000	0.053268	0.878934
# 2	0.648091	0.053268	1.000000	0.038109
# 3	0.012889	0.878934	0.038109	1.000000

结

[2] 中主要讨论了为啥这种假设检验的类的方法不好, 并给出了贝叶斯的方案. 我到没觉得后者有多好, 但是其关于假设检验的论断倒是颇为有趣. \(p\) 值不代表 \(H_0\) 成立的概率!

posted @ 2022-05-17 23:40  馒头and花卷  阅读(357)  评论(0)  编辑  收藏  举报