Neural Collaborative Filtering

目录

• 概
• 主要内容
  • 出发点
  • Neural CF
  • GMF and MLP
  • 其它细节
• 代码

He X., Liao L., Zhang H., Nie L., Hu X. and Chua T. Neural collaborative filtering. In International World Wide Web Conference (WWW), 2017.

概

对用户和物品隐变量分别建模, 然后协同过滤.

主要内容

令 \(Y \in \mathbb{R}^{M \times N}\)表示 user-item 的交互矩阵, 其中若二者存在交互则 \(y_{ui} = 1\), 否则 \(y_{ui} = 0\). 需要注意的是, \(y_{ui} = 0\) 并不能代表用户 \(u\) 对于物品 \(i\) 不感兴趣, 有可能只是单纯没有机会遇到而已. 本文就是希望预测这些'缺失'的部分:

\[\hat{y}_{ui}. \]

出发点

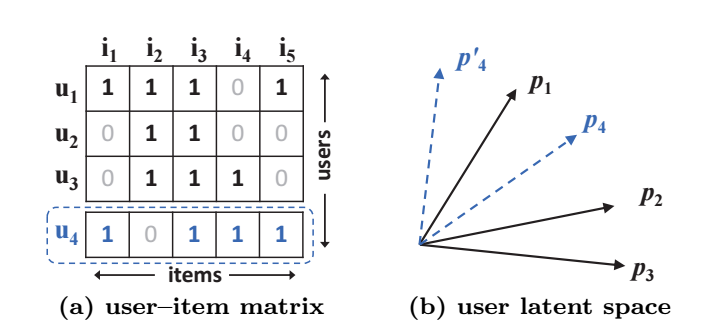
传统的基于矩阵分解的协同过滤可以理解为

\[\hat{y}_{ui} = f(u, i | \bm{p}_u, \bm{q}_i) = \bm{p}_u^T \bm{q}_i. \]

其中\(\bm{p}_u, \bm{q}_i \in \mathbb{R}^K\)分别表述用户 \(u\) 和物品 \(i\) 的隐变量.

倘若我们以 Jaccard coeffcient 来表述用户 \(i\), \(j\) 间的相似度

\[s_{ij} = \frac{|R_i \cap R_j |}{|R_i \cup R_j|}, \]

其中 \(R_u = \{j: y_{uj} = 1\}\).

那么自然的, 我会希望 \(\bm{p}_i, \bm{p}_j\)的内积尽可能满足这一相似度, 即

\[\bm{p}_i^T \bm{p}_j = s_{ij}. \]

现在, 让我们以上图为例来说明这一方法的局限性. 此时有

\[s_{23}(0.66) > s_{12}(0.5) > s_{13}(0.4), \]

故隐变量\(\bm{p}_1, \bm{p}_2, \bm{p}_3 \in \mathbb{R}^2\) (b) 方式排列, 此时我们再考虑 \(u_4\) 的隐变量. 我们可以发现, 找不到合适的 \(\bm{p}_4\) 服从

\[s_{41}(0.6) > s_{43}(0.4) > s_{42}(0.2). \]

这说明了基于矩阵分解这种简单的模式过于简单了.

Neural CF

如上图所示, Neural CF 流程如下:

1. 对于用户 \(u\) 和物品 \(i\), 分别获取各自 embedding \(\bm{p}_u, \bm{q}_i\);
2. 连接二者:

\[\bm{z}_1 = \phi(\bm{p}_u, \bm{q}_i) = \left [ \begin{array}{c} \bm{p}_u \\ \bm{q}_i \end{array} \right]; \]

3. 通过MLP提取特征

\[\bm{z}_2 = \phi_2(\bm{z}_1) = a_2 (W_2^T \bm{z}_1 + \bm{b}_2) \\ \cdots \\ \bm{z}_L = \phi_L(\bm{z}_{L-1}) = a_L (W_L^T \bm{z}_{L-1} + \bm{b}_L); \]

4. 逻辑斯蒂回归:

\[\hat{y}_{ui} = \sigma(h^T \bm{z}_L). \]

GMF and MLP

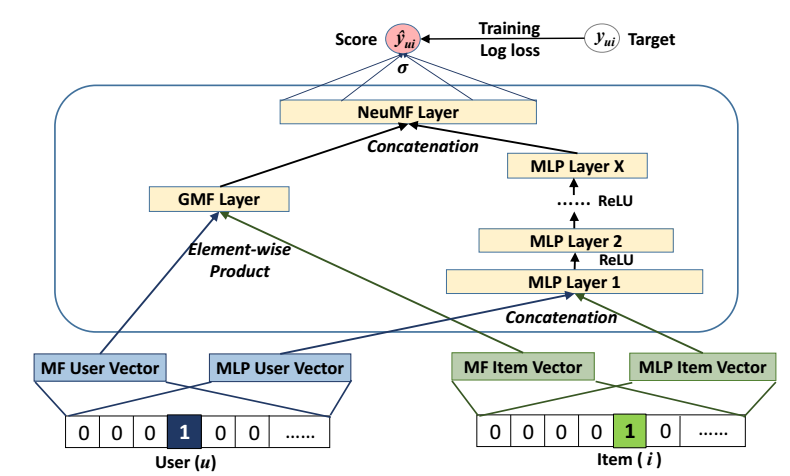
为了进一步用上隐变量的交叉信息, 作者融合了左端的 GMF:

1. 对于用户 \(u\) 和物品 \(i\), 分别获取各自 embedding \(\bm{p}_u, \bm{q}_i\) (注意, 该embedding 和 MLP的是独立的);
2. 交叉二者:

\[\bm{z}^{GMF} = \phi_1(\bm{p}_u, \bm{q}_i) = \bm{p}_u \odot \bm{q}_i, \]

其中\(\odot\)表逐元素相乘;

再结合右端 MLP 所提取的特征 \(\bm{z}^{MLP}\), 最后预测模型为

\[\hat{y}_{ui} = \sigma(\bm{h}^T \left [ \begin{array}{c} \bm{z}^{GMF} \\ \bm{z}^{MLP} \end{array} \right] ). \]

其它细节

1. 损失采用的是BCE:

\[L = -\sum_{(u, i) \in \mathcal{Y} \cup \mathcal{Y}^{-}} y_{ui} \log \hat{y}_{ui} + (1 - y_{ui}) \log (1 - \hat{y}_{ui}), \]

其中 \(\mathcal{Y}^{-}\)表示未观测到的交互 \(y_{ui} = 0\), 每次迭代采样部分得到.

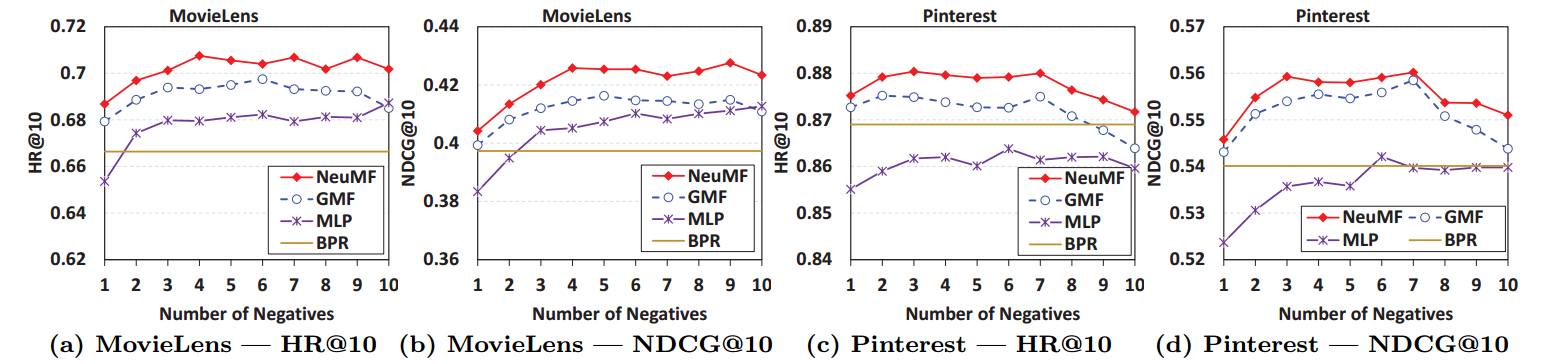
可见, 充分的负样本是必要的.

2. 先对 GMF 和 MLP 部分独立预训练, 然后再融合.

3. MLP 中激活函数选用 ReLU 而非 Sigmoid, Tanh.

4. 预训练采用 Adam, 然后正式训练采用不带momentum的SGD.

代码

原文代码

PyTorch