Multiple-gradient descent algorithm (MGDA) for multiobjective optimization

目录

• 概
• 主要内容
  • Pareto
  • MGDA

D\acute{e}sid\acute{e}ri J.-A. Multiple-gradient descent algorithm (MGDA) for multiobjective optimization. Comptes Rendus Mathematique, vol. 350, pp. 313–318, 2012.

概

本文尝试同时解决 \(n\) 个任务: \(J_i (\theta), i=1,2,\cdots, n\), 其中 \(\theta \in \mathbb{R}^N, n \le N\).

主要内容

\(J \in C^1\): 光滑.

Pareto

• Pareto 最优
  我们称 \(\theta^*\)是 Pareto 最优的, 当不存在\(\theta\)使得

\[J_{i}(\theta^*) \ge J_{i}(\theta), \quad \forall i \\ J_{i}(\theta^*) > J_{i}(\theta), \quad \exist i. \]

• Pareto-stationarity
  \(\theta\)是可行域\(\Omega\)中的一个内点, \(u_i := \nabla J_i(\theta)\)为其上的导数, 若有

\[\sum_{i} \alpha_i u_i = 0, \quad \sum_{i} \alpha_i = 1, \: \alpha_i \ge 0 \: \forall i \]

成立, 则称在\(\theta\)处是Pareto-stationarity的.

Lemma 1.2: 如果\(\theta\)是Pareto最优的, 则其也是Pareto-stationarity的.

证明思路是对 \(r = \text{rank}(\{u_i\}_{1\le i \le n})\) 进行分类讨论, 需要说明的是, 如果 \(\theta\) 是 Pareto 最优的, 则 $ r < n$ (通过KKT (LICQ)可知).

MGDA

MGDA的思路是在每一个阶段, 寻找合适的方向

\[w \in \bar{U} = \{u \in \mathbb{R}^N| u = \sum_{i=1}^n \alpha_i u_i; \: \sum_i \alpha_i = 1, \: \alpha_i \ge 0 \: \forall i \}, \]

且满足

\[w^T \nabla J_i(\theta) \ge 0, \]

即此时沿着\(w\)方向走对于所有目标而言都是没有坏处的.
实际上, 满足下面的 \(w\) 就是一个合适的(反)方向:

\[w = \mathop{\arg \min} \limits_{u \in \bar{U}} \|u\|_2^2, \]

则有下列性质成立:

Lemma 2.1: \(u^T w \ge \|w\|_2^2, \: \forall u \in \bar{U}\).

Theorem 2.2: \(w\) 有两种情况:

1. \(w = \bm{0}\), 此时 \(\theta\) 是 Pareto-stationarity的;
2. \(w \not = \bm{0}\), 此时 \(-w\)对于所有的\(J_i\)都是一个梯度下降的方向, 倘若\(w\)为\(\bar{U}\)的一个内点, 则有

\[u_i^T w = \|w\|_2^2 \]

成立.

---

对于第一种情况是显然的, 第二种情况的证明只需注意到:

\[w = \sum_i \alpha_i u_i, \]

其中\(\alpha_i\)可通过求解

\[\min_{\alpha_i} \|u\|_2^2 \\ \mathrm{s.t.} \: u \in \bar{U} \]

得到.
由于\(u\)是内点, 故满足KKT条件:

\[L(\alpha, \lambda) = \|u(\alpha)\|_2^2 + \lambda (\sum_{i=1}^n \alpha_i - 1) \\ \frac{\partial{L}}{\partial \alpha_i} = 2u^T u_i + \lambda = 0, \: \forall i, \lambda \not = 0. \]

故此时有

\[w^T u_i = -\frac{\lambda}{2}, \]

\[w^Tw = \sum_{i}\alpha_i w^T u_i = \sum_i \alpha_i (-\frac{\lambda}{2}) = -\frac{\lambda}{2}. \]

---

故, 每一次迭代, 我们只需找到 \(\bar{U}\)中模长最小的元素即可, 需要注意的是, 这个最小值是唯一的.
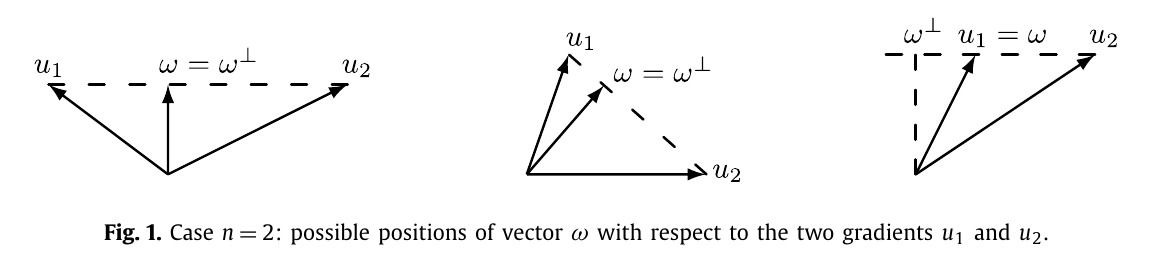
下图给出了 \(n=2\) 的三种情况: