Factorization Machines

目录

• 概
• 主要内容
  • FM
  • 优化
  • 扩展

Rendle S. Factorization machines. In IEEE International Conference on Data Mining (ICDM), 2010

概

SVM在很多领域都有应用, 却在推荐系统中没有什么特别好的效果, 作者认为主要原因是推荐系统的数据过于稀疏的原因. 因此, 本文提出FM来解决这一问题(其实从现阶段来看, 可以看成是embedding的一个扩展吧).

主要内容

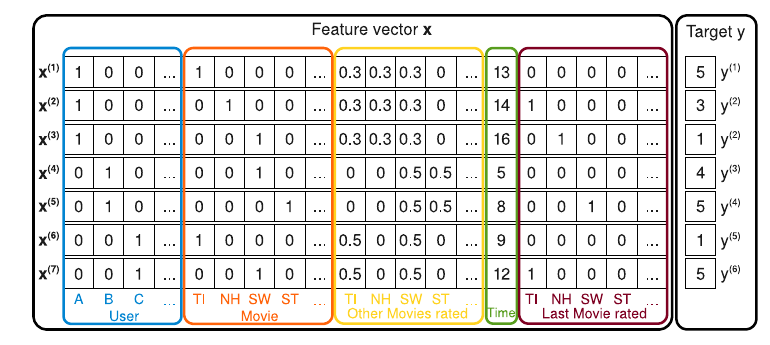
如上图所示, 每一行\(\mathbf{x} \in \mathbb{R}^n\)是一条数据, 其由下列构成:

• User: 用户 \(u\), one-hot 向量;
• Movie: 用户所打分的电影 \(i\), one-hot 向量;
• Other Movies rated: 其它打过分的矩阵 (normalzied 后)
• Time: 打分的时间;
• Last Movie rated: 对电影 \(i\) 打分之前所打分的电影 \(j\), one-hot 向量;
• Target y: 打分.

举个例子, \(\mathrm{x}^{(1)}, \mathrm{x}^{(2)}, \mathrm{x}^{(3)}\)分别是用户A为电影Titanic, Notting Hill, Star Wars打分的情况, 因为在为 Notting Hill 打分前所打分的电影为 Titanic, 所以 Last Movie rated 对应位置为 1, 其余为 0.

可见上述的数据是相当稀疏的.

FM

FM的预测公式如下:

\[\hat{y}(\mathbf{x}) := w_0 + \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i + 1}^n \mathbf{v}_i^T \mathbf{v}_j x_i x_j. \]

注意到,

\[\sum_{i=1}^n \sum_{j=i + 1}^n \mathbf{v}_i^T \mathbf{v}_j x_i x_j = \frac{1}{2} \mathbf{x}^T V^T V \mathbf{x} - \frac{1}{2} \sum_{i=1}^n \mathbf{v}_i^T \mathbf{v}_i x_i x_j. \]

实际上, FM 就是对一元特征\(x_i\)和二元特征\(x_ix_j\)的一个线性回归. 我个人感觉 \(\mathbf{v}_i \in \mathbb{R}^k\)可以看成特征\(x_i\)的一个embedding, 由或者 \(V^T V \in \mathbb{R}^{n \times n}\)可以看成是相关矩阵\(X^TX\)的一个近似.

通过和下列普通的回归的方式进行比较, 可以窥见其优势:

\[\hat{y}_{reg}(\bm{x}) = w_0 + \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n w_{ij} x_i x_j. \]

对于仅包含user和moive特征的\(\mathbf{x}\), 而言

\[\hat{y}(\mathbf{x}) = w_0 + w_u + w_i + \mathbf{v}_u^T \mathbf{v}_i \\ \hat{y}_{reg} (\mathbf{x}) = w_0 + w_u + w_i + w_{ui}. \]

想要训练\(w_{ui}\), 那必须由用户\(u\)为电影\(i\)进行过打分, 这意味着该模型几乎没有泛化性, 反之, FM的\(\mathbf{v}_u, \mathbf{v}_i\)会通过用户\(u\)的各打分数据和电影\(i\)的被打分数据进行训练, 显然更可靠.

优化

• 自然, 可以沿用回归的思想, 通过诸如MSE进行拟合;
• 如果是预测点击率, 也可以通过逻辑斯蒂回归等方式拟合;
• 作者是通过SGD进行训练的.

扩展

上面引入了二元的特征, 自然可以推广到 \(x_{i_1} x_{i_2} \cdots x_{i_d}\) 这种 \(d\) 元的模式, 只是这种方式个人感觉组合数有点夸张了. 另外作者和SVM进行了比较, 其实想说明的点就是之前的, 这里就不多赘述了.