Adversarial Vertex Mixup: Toward Better Adversarially Robust Generalization
概
本文提出类注意哦那个 AVmixup 方法用以提高鲁棒的泛化性.
主要内容
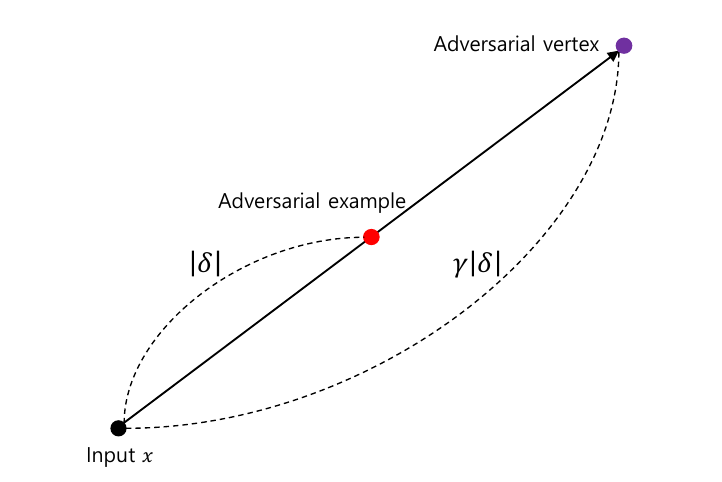
通常, 我们会选择用 \(x + \delta\) 来作为对抗样本, 但是这个方式的对抗样本缺乏多样性, 故会导致较差的鲁棒泛化性. 本文采用(启发自 mixup)
\[x' = \alpha x + (1 - \alpha) x_{av}, \\
x_{av} = x + \gamma \cdot \delta_x,
\]
这里通常 \(\gamma \ge 1\), 即 \(x_{av}\) 是沿着\(\delta\)方向的一个延拓. 最后的对抗样本\(x'\)是在干净样本\(x'\)和这个延拓后的样本中选择的. 和 mixup, 给定其概率向量为
\[\bm{p} = \alpha \phi(y, \lambda_1) + (1 - \alpha) \phi(y, \lambda_2) \in \mathbb{R}^K.
\]
这里\(\phi\)是soft_label的函数, 其实 mixup 就是直接用的 \(y\), 作者这里用了最普通的label smoothing:
\[[\phi(y, \lambda)]_k =
\left \{
\begin{array}{ll}
\lambda & k = y \\
\frac{1 - \lambda}{K - 1} & k \not = y.
\end{array}
\right .
\]
算法:
- \(\delta \leftarrow \mathcal{G}(x, y; \theta)\);
- \(x_{av} \leftarrow x + \gamma \delta\), \(\alpha \sim \mathcal{U}[0, 1]\);
- \(x' \leftarrow \alpha x + (1 - \alpha) x_{av}\);
- \(\bm{p} \leftarrow \alpha \phi(y, \lambda_1) + (1 - \alpha)(y, \lambda_2)\);
- \(\theta \leftarrow \theta - \tau \frac{1}{n}\sum_{i=1}^n \nabla_{\theta} \mathcal{L}(x'_i, \bm{p}_i; \theta)\).
注: 作者给出了在高斯分布上的分析, 但是我顺不起来, 这里就不提了.
注: 虽然这个方法有点破坏梯度的感觉, 但是其在AutoAttack下依然是有尚可的鲁棒性的, 代价仅仅是几个点的自然精度的损失, 从这个角度来说其实挺好的.
