Learning to Augment for Casual User Recommendation
概
作者认为, 由于数据的偏向, 即 core 用户 (比如时常购物的) 的数据比较多, 而 causal 用户 (购物没有特别规律的) 比较少, 容易造成在 causal 用户上的推荐结果不是特别好. 对推荐系统的序列数据进行数据增强 (保留 or 删除 部分) 使得推荐系统能够对 casual 用户也能照顾得当.
主要内容
符号
- \(\mathcal{U} = \{u_1, u_2, \cdots, u_{|\mathcal{U}|}\}\), 用户;
- \(\mathcal{I} = \{i_1, i_2, \cdots, i_{|\mathcal{I}|} \}\), 物品;
- \(\mathcal{U} = \mathcal{U}_{core} \cup \mathcal{U}_{causal}\);
- \(S_u = [i_{u,1}, i_{u, 2}, \cdots, i_{u, n}]\), 序, \(i_{u, p} \in \mathcal{I}\)表示用户\(u\)历史购买的第\(p\)件商品;
- \(S_{u, [1:p]} = [i_{u,1}, i_{u, 2}, \cdots, i_{u, p}]\);
- \(\hat{\bm{y}}_{u, j} := f(S_{u, [1:j-1]}; \theta) \in \mathbb{R}^{|\mathcal{I}|}\), 根据历史交易记录\(S_{u, [1:j-1]}\)下预测第\(j\)次购买的商品的得分(长度为\(|\mathcal{I}|\)的向量, 每个元素代表对应商品的得分).
Data Augmentor
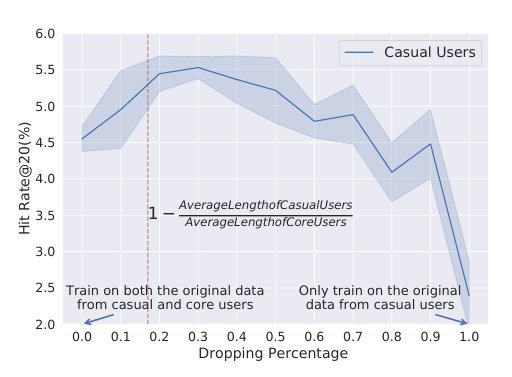
- 出发点: 作者认为那些core 用户由于频繁的交易, 使得推荐系统普遍会偏向这部分人群, 导致对 casual 的推荐的效果不是那么好, 作者希望通过对 \(S_{core}\) 进行数据增强来缓解这一问题. 事实上, 这一根据成立可以首先通过下图得知. 作者随机地丢弃 \(S_{core}\) 中部分交易记录, 其结果呈现一个先增后减的过程.
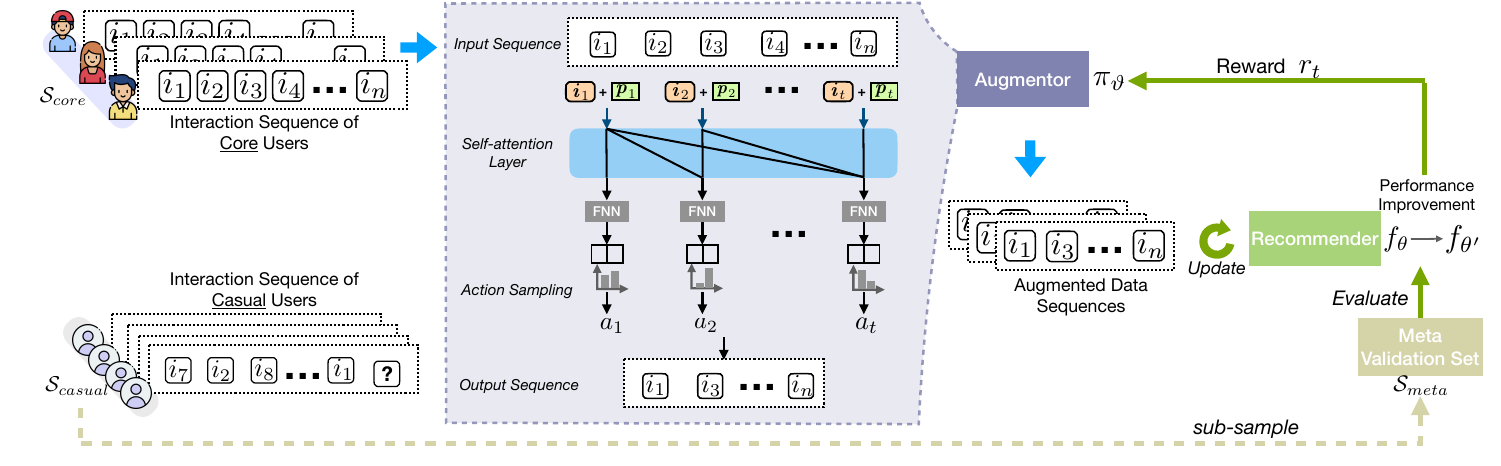
- 输入 \(S_{u} = [i_{u, 1}, \cdots, i_{u, t}]\);
- 对 \(i_{u, k}\) 取得其 embedding:
\[\bm{e}_{k} = \bm{i}_k + \bm{p}_k,
\]
其中 \(\bm{i}_k\) 是 item-embedding, \(\bm{p}_k\) 是 positional embedding;
- 通过自注意力获取 \(S_{u, [:k]}\) 的 embedding:
\[\bm{h}_k = \sum_{j \le k}\sigma_{kj} W_V \bm{e}_j \\
\sigma_{kj} = \frac{S(W_Q \bm{e}_k, W_K \bm{e}_j)}{\sum_{j \le k} S(W_Q \bm{e}_k, W_K \bm{e}_j)},
\]
这里作者用的不是传统的 \(S(\cdot) = \exp(\cdot)\)(即softmax), 而是 scaled dot-product:
\[S(\bm{a}, \bm{b}) = \bm{a}^T\bm{b} / \sqrt{D}, \bm{a}, \bm{b} \in \mathbb{R}^D.
\]
- 通过 FNN 获得 第\(k\) 的点augmentaion 操作的概率:
\[\pi (\cdot|\bm{h}_k; \Theta) = \mathrm{softmax}(W_A \bm{h}_k) \in \mathbb{R}^{|\mathcal{A}|},
\]
文中只考虑了 \(\mathcal{A} = \{remove, keep\}\) 这两种操作.
- 通过概率 \(\pi\) 选择 某个 action \(a_{u, k}\), 保留或者删除 \(i_{u, k}\), 最后得到augmented后的数据 \(\tilde{S}_{core}\);
- 利用这些数据微调 \(f_{\theta}\), 结果为$ f_{\theta'}$;
- 计算在 验证集 (用 \(S_{causal}\)) 构成上的 reward:
\[r_t = \mathrm{HT}(f_{\theta'}, S_{meta}) - \mathrm[HT](f_{\theta}, S_{meta});
\]
- 利用 policy gradient 更新 \(\Theta\):
\[\nabla_{\Theta} \tilde{J}(\Theta) = r_t \sum_{u \in \mathcal{S}_B} \sum_{k=1}^{|S_u|} \nabla_{\Theta} \log \pi (a_{u, k}|\bm{h}_{k}; \Theta);
\]
- 训练\(\pi\)一定次数后, 利用 \(S_{core}, S_{causal}\)更新系统\(f_{\theta}\):
\[\ell(\theta) = -\sum_{u \in \mathcal{U}} \sum_{j=1}^{|S_u|} [\log (\sigma (\hat{\bm{y}}_{u, j}^{i_{u, j}})) + \sum_{k \not \in S_u} \log (1 - \sigma (\hat{\bm{y}}_{u, j}^{k})) ].
\]
注: Policy Gradient (强化学习):
\[\max_{\theta} \bar{R} := \mathbb{E}_{a \sim \pi_{\theta}(a)} [R(a)],
\]
\[\begin{array}{ll}
\nabla_{\theta} \mathbb{E}_{a \sim \pi_{\theta}(a)} [R(a)]
&= \int R(a) \nabla_{\theta} \pi_{\theta}(a) \\
&= \int R(a) \pi_{\theta}(a) \nabla_{\theta} \log \pi_{\theta}(a) \\
&= \mathbb{E}_{a \sim \pi_{\theta}(a)} [R(a) \nabla \log \pi_{\theta}(a)] \\
&\approx \frac{1}{n} \sum_{i=1}^n [R(a_i) \nabla \log \pi_{\theta}(a_i)].
\end{array}
\]
评价指标
注: 上面的 HT 表示 Hit Rate, 对于\(u\)而言, 假设\(y_u\)为真实的下次交易的物品, 如果它出现在我们所推荐的前K个物品中, 则 HT@K = 1, 否则为0.


