Do We Need Zero Training Loss After Achieving Zero Training Error?
概
一味的最小化训练损失甚至趋于0往往会造成严重的过拟合. 作者退而求其次, 选择优化如下替代损失
\[\tag{1}
\tilde{J}(\theta) = |J(\theta) - b | + b,
\]
一旦\(J(\theta) < b\), 原本的梯度下降就变成了梯度上升了. 作者认为, 在合理的阈值\(b\)附近振荡有利于参数的平滑.
主要内容
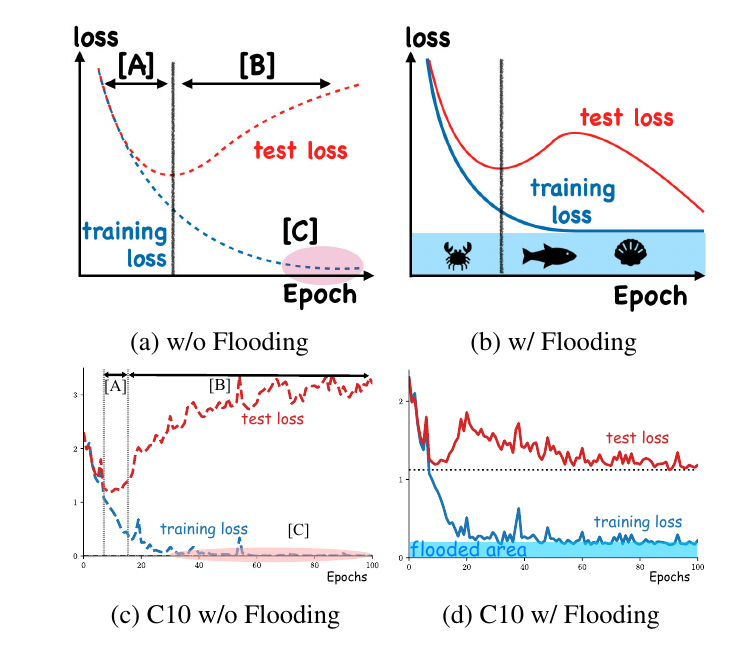
回到更实际的mini-batch的训练方式中去, 定义损失:
\[\ell(x, y; \theta),
\]
理想的risk为
\[R(\theta) := \mathbb{E}_{(x, y)} [\ell(x, y; \theta)],
\]
与之对应的经验risk:
\[\hat{R}(\theta) := \frac{1}{n}\sum_{i=1}^n \ell(x_i, y_i; \theta).
\]
然后本文所定义的 flooding empirical risk:
\[\tag{2}
\tilde{R}(\theta) = |\hat{R}(\theta) - b| + b.
\]
优化这类损失和原来的损失差别在于, 一旦\(\hat{R}(\theta) < b\)之后, 二者的梯度就相反了, 可以预想到此时损失会在\(b\)附近振荡. 作者认为者能够帮助模型收敛到一个更加光滑的参数空间中去(因而更有利于泛化性), 这可以从作者的实验中窥探一二:

可以发现, 相较于w/o flooding 的情况, 使用 (2) 让模型的输出关于参数更加光滑和平坦了.
理论
定理1: 对于任意的\(\theta\), 若阈值\(b\)满足\(b \le R(\theta)\), 则
\[\mathbb{E}[(\hat{R}(\theta)) - R(\theta)]^2 \ge \mathbb{E}[\tilde{R}(\theta) - R(\theta)]^2.
\]
这个结果其实很一般, 因为一旦\(\hat{R}(\theta) > b \rightarrow \hat{R}(\theta) = \tilde{R}(\theta)\), 所以只需要考虑\(\hat{R}(\theta) < b \le R(\theta)\)的情况,
另外, 感觉后续的文章的解释更加靠谱一点.
代码
outputs = model(inputs)
loss = criterion(outputs, labels)
flood = (loss-b).abs()+b # This is it!
optimizer.zero_grad()
flood.backward()
optimizer.step()


