Flooding-X: improving bert’s resistance to adversarial attacks via loss-restricted fine-tuning.
概
作者认为通过 flooding 能够使得 loss landscape 平滑, 这有利于抵抗对抗攻击. 不同于原flooding方法, 梯度下降还是上升是通过一个 gradient accordance 的指标来满足的.
主要内容
原Flooding方法的作用
Flooding是将损失替换为:
\[\tilde{J}(\theta) = |J(\theta) - b| + b,
\]
相应的, empirical risk为
\[\tilde{R}(\bm{f}) = |\hat{R}(\bm{f}) - b| + b.
\]
假设在第n个mini-batch训练损失触及阈值\(b\), 即
\[\bm{\theta}_n = \bm{\theta}_{n-1} - \epsilon \bm{g}(\bm{\theta}_{n-1}), \\
\bm{\theta}_{n+1} = \bm{\theta}_{n} + \epsilon \bm{g}(\bm{\theta}_{n}), \\
\]
第n+1个mini-batch的时候梯度反向. 其中\(\bm{g}(\bm{\theta}) = \nabla_{\bm{\theta}} J(\bm{\theta})\).
则
\[\begin{array}{ll}
\bm{\theta}_{n+1}
&= \bm{\theta}_{n-1} - \epsilon \bm{g}(\bm{\theta}_{n-1}) + \epsilon \bm{g}(\bm{\theta}_{n-1} - \epsilon \bm{g}_{\bm{\theta}_{n-1}}) \\
&\approx \bm{\theta}_{n-1} - \frac{\epsilon^2}{2} \nabla_{\bm{\theta}}\|\bm{g}(\bm{\theta}_{n-1})\|^2.
\end{array}
\]
故, Flooding可以理解为是添加了一个\(\|\bm{g}(\bm{\theta})\|^2\)的正则项, 一阶导数和函数的光滑性相挂钩, 这解释了为啥Flooding是有效的.
\(b\)的选择
实际上, 我们只要知道在某个batch中, 应该采取梯度下降(即最小化损失\(J\))还是梯度上升(即最大化损失\(J\))即可, 不一定非得找到最优的\(b\). 本文就是通过 gradient accordance 来判断.
我们首先考察参数更新前后\(\bm{\theta}\)和\(\bm{\theta}':=\bm{\theta} - \epsilon \bm{g}\), 损失\(\mathcal{L}(f(x), y)\)的变换情况:
\[\Delta \mathcal{L} =
\mathcal{L}(f(x; \bm{\theta}'), y)
-\mathcal{L}(f(x; \bm{\theta}), y).
\]
由于
\[f(x; \bm{\theta}') = f(x; \bm{\theta}) - \epsilon \nabla_{\theta}^Tf \bm{g} + \mathcal{O}(\epsilon^2) \rightarrow
f(x; \bm{\theta}) = f(x; \bm{\theta}') + \underbrace{\epsilon \nabla_{\theta}^Tf \bm{g} + \mathcal{O}(\epsilon^2)}_{T(x;\theta)},
\]
故
\[\begin{array}{ll}
\mathcal{L}(f(x; \bm{\theta}), y)
&=\mathcal{L}(f(x; \bm{\theta}') + T(x;\theta), y) \\
&=\mathcal{L}(f(x; \bm{\theta}'), y)
+\frac{\partial \mathcal{L}}{\partial f} T + \mathcal{O}(T^2).
\end{array}
\]
于是
\[\begin{array}{ll}
\Delta \mathcal{L}
&=-\frac{\partial \mathcal{L}}{\partial f} T(x; \bm{\theta}) - \mathcal{O}(T^2)\\
&=-\epsilon \bm{g}^T \: (\frac{\partial \mathcal{L}}{\partial f}\nabla_{\theta}f) - \mathcal{O}(T^2)\\
&\approx - \epsilon \bm{g}^T \bm{g}' \quad \leftarrow \bm{g}':=\frac{\partial \mathcal{L}}{\partial f}\nabla_{\theta}f.
\end{array}
\]
有了上面的工具, 让我们来考察优化一个样本对另一个样本的影响, 假设我们要优化
\[\mathcal{L}(f(x_1), y),
\]
对于
\[\mathcal{L}(f(x_2), y).
\]
此时:
\[\bm{g} = \nabla_{\theta} \mathcal{L}(f(x_1), y), \:
\bm{g}' = \nabla_{\theta} \mathcal{L}(f(x_2), y).
\]
显然, 当\(\bm{g}, \bm{g}'\)的方向一致的时候, 优化\(x_1\)的同时对于\(x_2\)也是有利的, 否则是有害的. 基于此发现我们定义一个epoch的 gradient accordance:
- 将当前batch\(B\)的样本\(X\)按照类别\(1,2,\cdots, k\)拆分为\(k\)组:
\[X = X_1 \cup X_2 \cup \cdots \cup X_k;
\]
- 定义sub-batch:
\[B^s := \{X_s, s\},
\]
这里\(X_s\)的样本均是第\(s\)类的;
3. 定义 class accordance:
\[C(B^1, B^2) = \mathbb{E}[\cos (\bm{g}_1, \bm{g}_2)],
\]
\(\bm{g}_1, \bm{g}_2\)分别采样自两个sub-batch;
- 假设当前epoch有\(N\)个batch \(B_1, B_2, \cdots, B_N\), 任意两个batch \(B_s, B_t\)之间的accordance 定义为:
\[S_{batch \: accd}(B_s, B_t) := \frac{1}{k(k - 1)} \sum_{i=1}^k \sum_{j\not =i} C(B_s^i, B_t^j);
\]
- 则一个epoch的 gradient accordance 定义为:
\[S_{epoch \: accd} := \frac{1}{N(N - 1)} \sum_{s=1}^N \sum_{t\not =s} S_{batch \: accd}(B_s, B_t).
\]
故, 每个epoch结束后计算\(S_{epoch \: accd}\), 如果其为正, 这表示应该继续最小化损失, 否则已经达到过拟合阶段, 应当最大化损失.
疑问: 一个epoch梯度上升难道不会产生很严重的后果? 而且用batch accordance 不就不用保存以前的那些? 而且作者总共就训练(finetune) 10 epochs, 感觉很奇怪. 应该没理解错吧, 作者的图的横坐标也都是 epoch 为间隔的.
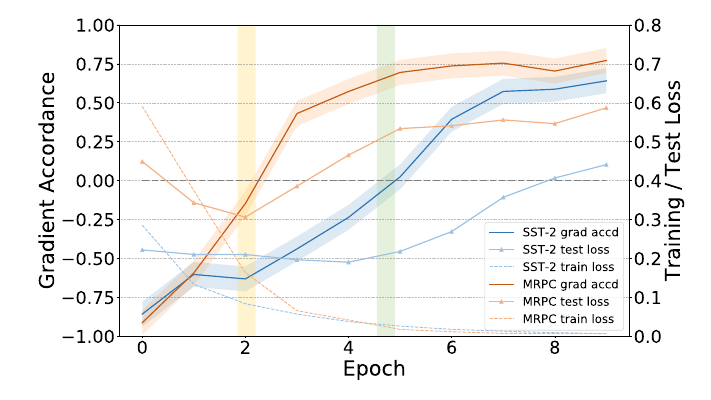
如图, 是不是因为一开始预训练模型比较一般, 所以先梯度上升跳出局部最优再搞优化?



