Exploring Memorization in Adversarial Training
概
大家知道, 即使是随机的标签\(\{(x_i, y_i)\}_{i=1}^N\) (\(y_i\)是随机赋予的), 普通的网络\(f(\cdot)\)也能够很好地拟合(训练精度几乎达到100%). 本文发现, 即使是对抗训练, 网络\(f\)也能够很好地拟合.
作者认为, 这是导致过拟合的元凶, 利用 temporal ensembling (TE) 可以缓解这一点.
主要内容
PGD-AT:
\[\min_{\theta} \: \sum_{i=1}^n \max_{\|x_i'\| \le \epsilon} \mathcal{L}_{ce}(f_{\theta}(x_i'), y_i).
\]
TRADES:
\[\min_{\theta} \: \sum_{i=1}^n \mathcal{L}_{ce}(f_{\theta}(x_i), y_i) + \beta \cdot \max_{\|x_i'\| \le \epsilon} \mathbf{KL} (f_{\theta}(x_i)\|f_{\theta}(x_i')).
\]
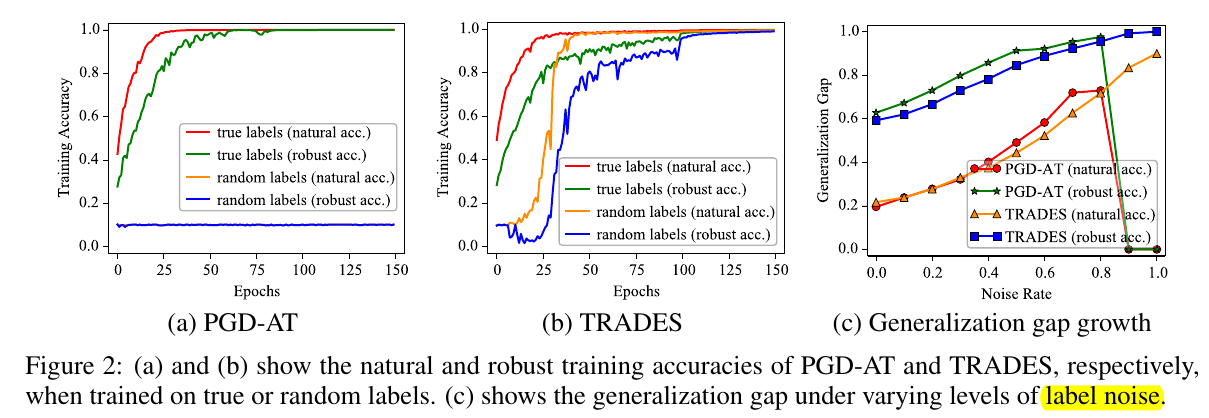
通过比较(a), (b)可以发现, 当通过随机标签进行训练的时候, TRADES的训练精度几乎可以达到100%, 这说明网络的拟合能力是完全足够的. 另一方面, PGD-AT不行的原因是, 其损失函数仅包含对抗损失, 训练被杀死了.
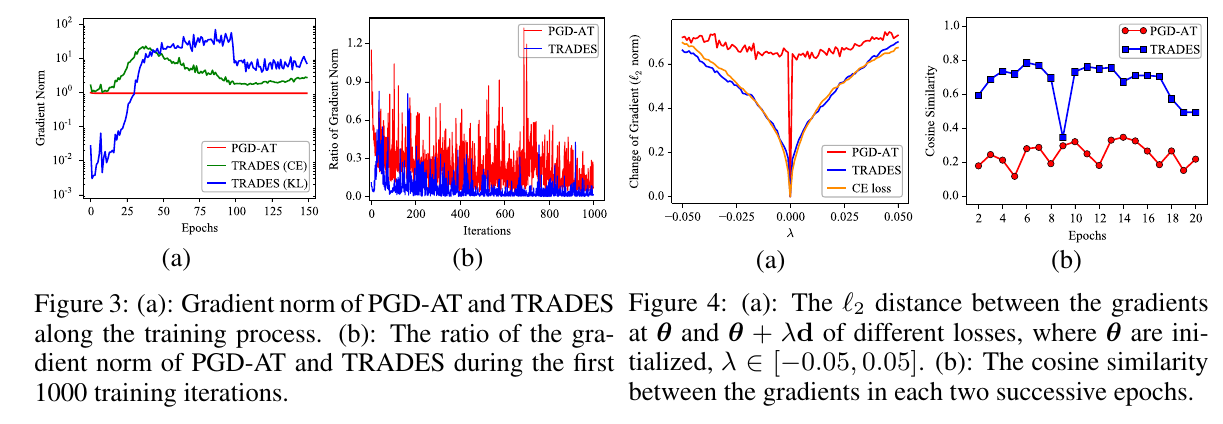
作者发现, 该主要原因是PGD-AT利用随即标签训练前后的参数扰动变化过大, 可以理解为当前点的梯度几乎是没有任何参考意义的, 这导致训练被杀死.
相比之下, TRADES因为还有普通样本的交叉熵损失, 所以比较稳定.
过拟合
既然神经网络有如此的强大的拟合能力, 这在一定程度上解释了对抗训练为什么会这么容易出现过拟合. 设想, 因为我们对抗训练的时候, 一直采用的标签训练, 但是对于因为\(\|x' - x\|\le \epsilon\), 当\(\epsilon\)比较大的时候, 用标签似乎就有点过于强硬了. 所以作者采用了 temporal ensembling来缓解:
\[\min_{\theta} \: \sum_{i=1}^n \max_{\|x_i'\| \le \epsilon} \{ \mathcal{L}_{ce}(f_{\theta}(x_i'), y_i) + w \cdot \|f_{\theta}(x_i') - \hat{p}_i\|_2^2\},
\]
其中
\[p_i \leftarrow \eta \cdot p_i + (1 - \eta) \cdot f_{\theta}(x) \\
\hat{p}_i = p_i / \|p_i\|_1,
\]
累积了过去的网络对这个样本的预测. 这意味着, 我们希望过去的预测和现在的能够尽可能保持一致性.
