Temporal Ensembling for Semi-Supervised Learning
概
本文提出两种半监督算法: \(\prod\)-model和temporal emsembling.
前者令统一样本的不同视图(通过不同数据增强和dropout得到)的特征接近,
后者则是通过滑动平均维护这些特征. 相较于前者, 后者更加稳定.
主要内容
训练集:
- 带标签数据 \(\{(x_i, y_i)\}_{i=1}^{M}\);
- 不带标签数据 \(\{x_j\}_{j=M + 1}^N\).
\(y \in \{1, 2, \cdots, C\}\).
数据增强: \(g(\cdot)\);
网络: \(f_{\theta}: x \rightarrow z\). (其中 \(z\) 为概率向量)
*-model


对于所有数据而言, \(x\)经过\(f\circ g\)得到两个不同的概率向量\(z, \tilde{z}\), 并利用均方损失:
\[\frac{1}{C}\|z - \tilde{z}\|^2
\]
迫使二者靠近.
对于带有标签的数据而言, 还有普通的交叉熵损失. 读者可能会有疑问, 为啥\(z, \tilde{z}\)不用交叉熵损失:
\[-\sum_{k=1}^C \tilde{z}_k \log z_k,
\]
作者没有明说, 只是说均方损失效果更好. 不过, 既然用均方损失, 那会不会用softmax之前的特征更合适?
Temporal ensembling
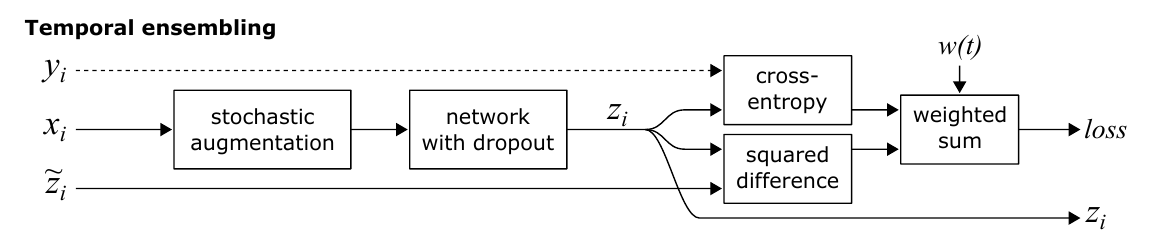

与之前不同的是, 目标向量\(\tilde{z}\)不是通过再次推断\(x\)得到的, 而是通过滑动平均
\[Z \leftarrow \alpha Z + (1 - \alpha) z
\]
加上偏置矫正?
\[\tilde{z} \leftarrow Z / (1 - \alpha^t).
\]
注意因为\(Z_0 = \tilde{z}\)初始化为0,
所以(归纳法)
\[Z_t = (1 - \alpha) \sum_{i=1}^t \alpha^{t - i} z_i,
\]
故
\[\sum_{k=1}^C [Z_t]_k = (1 - \alpha) \sum_{i=1}^t \alpha^{t - i} \sum_{k=1}^C [z_i]_k = (1 - \alpha) \sum_{i=1}^t \alpha^{t - i} = 1 - \alpha^t.
\]
所以这个校准可以保证\(\tilde{z}\)满足概率的性质.
超参数的选择
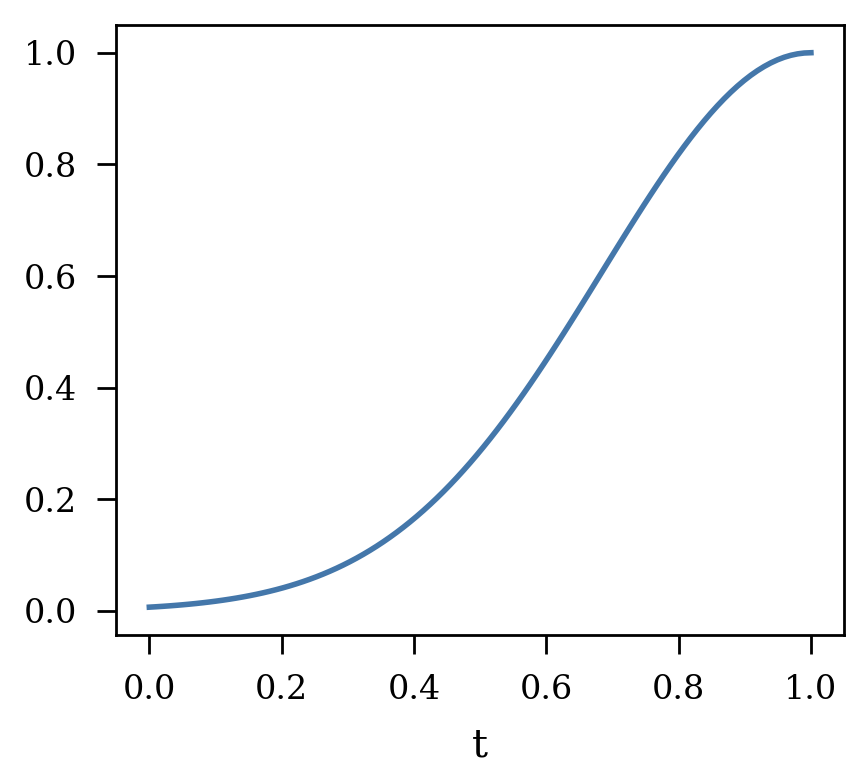
作者选择动量\(\alpha = 0.6\), 在初始的80个epochs内\(w(t)\)从\(0\)爬升到\(w_{max} \cdot M/N\), 具体方式为 Gaussian ramp-up:
\[w(t) =
\left \{
\begin{array}{l}
\exp [-5(1 - t)^2] \cdot (w_{max} \cdot M/ N) & t \in [0, 1] \\
w_{max} \cdot M / N & t > 1.
\end{array}
\right .
\]
注: \(t\)在前80个epoch内是线性增加到1的.