Xu H., Liu X., Wang W., Jain A. K. Tang J., Ding W., Wu Z. and Liu Z. Towards the memorization effect of neural networks in adversarial training. In International Conference on Learning Representations (ICLR), 2022.
概
作者将样本分为 typical 和 atypical (可以理解为较少的和其它类别相近的困难样本) 两类. 神经网络对于前者能够利用语义特征来区别, 而对于后者往往需要利用记忆. 对于标准训练来说, 记忆 atypical 的样本并不会降低网络的泛化能力. 对于对抗训练来说, 为了记忆 atypical 样本, 容易造成自然精度的下滑, 所以作者提出BAT来更细致地对待这些 atypcial 样本.
主要内容
typcial 和 atypical 样本
首先定义利用算法\(\mathcal{A}\)和数据集\(\mathcal{D}\)在样本\(x_i\)处的'memorization value':
\[\tag{1}
\mathrm{mem}(\mathcal{A}, \mathcal{D}, x_i)
=\mathop{\mathbf{Pr.}} \limits_{F \leftarrow \mathcal{A}(\mathcal{D})} (F(x_i) = y_i)
-\mathop{\mathbf{Pr.}} \limits_{F \leftarrow \mathcal{A}(\mathcal{D} \setminus x_i)} (F(x_i) = y_i).
\]
如果该值很大, 说明网络必须记忆这个样本, 否则难以正确识别出它 (也就是说这个样本的特征其实是脱离整个数据集的分布的).
上面的是对于训练集中的样本而言的, 对于测试集合的样本 \((x_j', y_j')\) 和训练集中的样本 $ (x_i, y_i)$ 有:
\[\tag{2}
\mathrm{infl}(\mathcal{A}, \mathcal{D}, x_i, x_j')
=\mathop{\mathbf{Pr.}} \limits_{F \leftarrow \mathcal{A}(\mathcal{D})} (F(x_j') = y_j')
-\mathop{\mathbf{Pr.}} \limits_{F \leftarrow \mathcal{A}(\mathcal{D} \setminus x_i)} (F(x_j') = y_j').
\]
给定阈值 \(t\), 我们定义 atpcial 训练样本和测试样本:
\[\mathcal{D}_{\mathrm{atyp}} := \{x_i \in \mathcal{D}| \mathrm{mem}(x_i) > t\}, \\
\mathcal{D}_{\mathrm{atyp}}' := \{x_j' \in \mathcal{D'}| \mathrm{infl}(x_i, x_j') > t, \: \forall x_i \in \mathcal{D}_{\mathrm{atyp}}\}.
\]
atypical 较差的泛化性
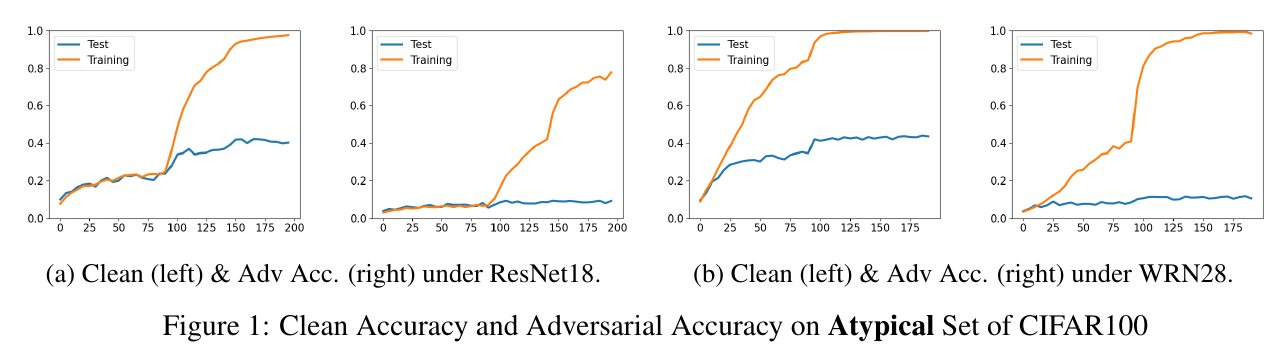
作者选择了 \(t=0.15\), 然后在整个数据集上进行训练, 可以发现:
- 无论是自然精度还是鲁棒性, 其Training的结果都很好, 这意味这ResNet18WRN28都有足够的表示能力;
- 随着训练精度的上升, 在 \(\mathcal{D}_{\mathrm{atyp}}'\)上的自然精度能够上升, 但是鲁棒性几乎没有变换, 说明记忆 atpyical 样本对于增强鲁棒性是无效的.
typcial 和 atypical 样本在鲁棒性上的冲突
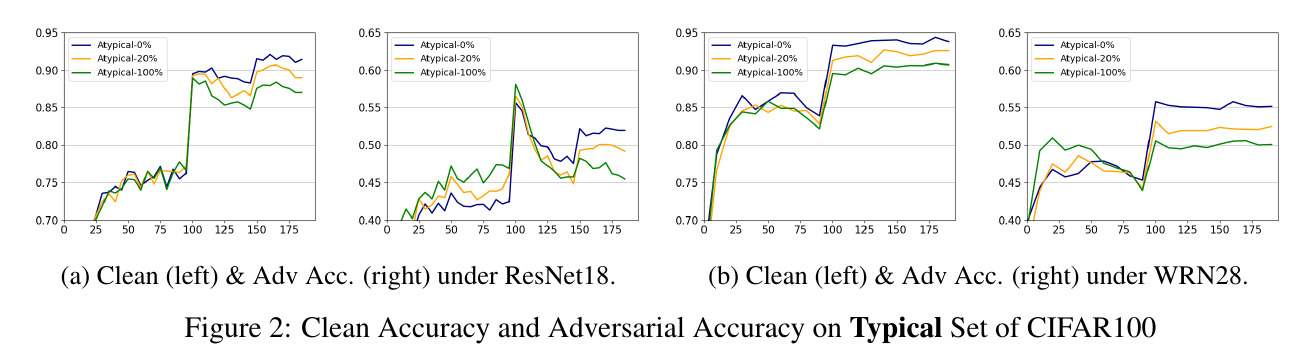
这里, 作者以 typical 样本为基础, 逐步添加 atypical 样本, 可以发现让网络去记忆这些 atypical 反而会造成对 typical 数据有效性. 作者认为, 这些 atypical 由于本身数目比较少, 然后又和别的类别比较接近, 区分难度大的特点, 导致网络想要去记忆这些样本反而会学习到更差的特征.
Benign Adversarial Training (BAT)
作者通过重加权和 Discrimination Loss 来解决这一问题.
cost-sensitive reweighting strategy
\[\left \{
\begin{array}{ll}
\exp(-\alpha \cdot q(x_i^{adv})) & \text{if } \mathrm{mem}(x_i) > t \text{ and } \mathrm{argmax}_k F_k(x_i^{adv}) \not = y \\
1 & \text{otherwise}.
\end{array}
\right .
\]
其中
\[q(x_i^{adv}) = \max_{k \not =y} F_k(x_i^{adv}).
\]
然后分类损失是:
\[\mathop{\arg \min} \limits_F \frac{1}{\sum_{i}w_i} \sum_{i} [w_i \cdot \mathcal{L}(F(x_i^{adv}), y_i)].
\]
discrimination loss
\[\mathcal{L}_{DL}(F) = \mathop{\mathbb{E}} \limits_{(x_i, y_i) (x_j, y_j), \{(x_b,y_b)\}_{b=1}^B} \Big[-\log \frac{e^{h^T(x_i^{adv}) h(x_j^{adv}) / \tau}}{\sum_{b=1}^B e^{h^T(x_i^{adv}) h(x_k^{adv}) / \tau}} \Big],
\]
其中
\[y_i = y_j, \\
y_b \not= y_i, \: b=1,2,\cdots, B, \\
\mathrm{mem}(x_i), \mathrm{mem}(x_j), \mathrm{mem}(x_b) < t.
\]
即该损失希望 typcial 样本的特征 \(h(x_i)\) (倒数第二层) 同类之间相互靠近, 不同类之间相互远离.
最后的损失是:
\[\mathop{\arg \min} \limits_F \frac{1}{\sum_{i}w_i} \sum_{i} [w_i \cdot \mathcal{L}(F(x_i^{adv}), y_i)] + \beta \cdot \mathcal{L}_{DL}(F).
\]
实验设置:
- \(\alpha = 1 | 2, \beta = 0.2\);
- 160 epochs, momentum=0.9, weight decay = 5e-4;
- lr=0.1, [80, 120] x 0.1
- CIFAR: \(8/255\); TinyImageNet: \(4/255\)
