Improving the Learning Speed of 2-Layer Neural Networks by Choosing Initial Values of the Adaptive Weights

目录

• 概
• 主要内容
  • 一维情形
    • 如何加速
  • 多维情形
• 代码

Nguyen D. and Widrow B. Improving the learning speed of 2-layer neural networks by choosing initial values of the adaptive weights. In International Joint Conference on Neural Networks (IJCNN), 1990.

概

本文提出了一种关于两层网络的权重初始化方法.

主要内容

假设我们想通过一个两层的网络

\[f(\bm{x}) = \sum_{i=1}^{H} v_i \tanh (\bm{w}_i^T \bm{x} + b_i), \]

拟合一个函数\(g(\bm{x})\).
其中 \(\bm{x}, \bm{w}_i \in \mathbb{R}^{d}\).

\[\tanh (x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}, \]

在\([-1, 1]\)之前是近似线性的.

为了方便讨论, 令\(f_i(\bm{x}) := v_i \tanh (\bm{w}_i^T \bm{x} + b_i)\).

一维情形

\[f(x) = \sum_{i=1}^{H} v_i \tanh (w_i x + b_i), \\ f_i(x) = v_i \tanh (w_i x + b_i). \]

不考虑\(\tanh\), 当\(x \in [-1, 1]\)时, 每个\(f_i(x)\)(近似)落在区间

\[[b_i - |w_i|, b_i + |w_i|] \]

之中. 该区间以\(b_i\)为中心, 大小为\(2|w_i|\).
所以总的网络可以看成是在每个区间内采样\(\xi_i\), 然后求和

\[f(x) = \sum_{i=1}^H v_i \xi_i. \]

倘若每个区间是差不离一致的, 那么就容易导致\(f(x)\)本身是很平坦的,

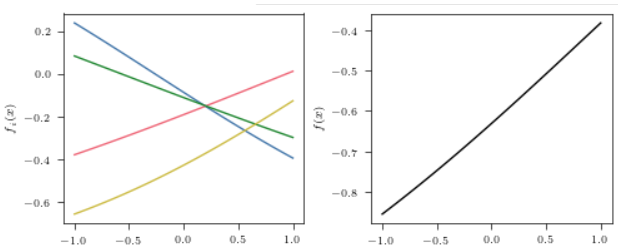
注: 文中还要平坦, 这个和初始化有关系, 不过既然都是近似线性的, 所以直线是正常的.

如何加速

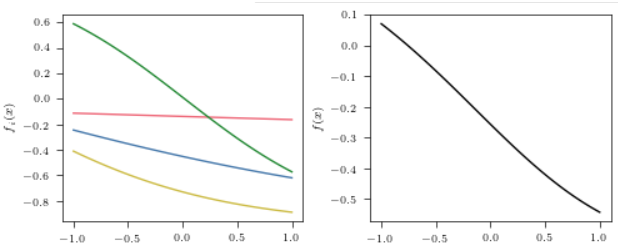
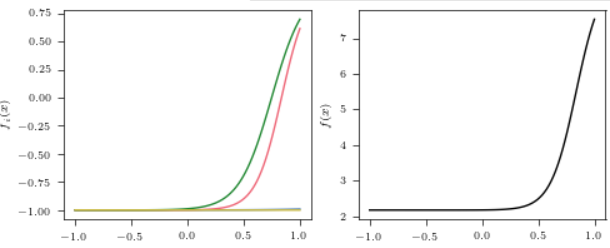
上面是的情况是权重 \(w_i, b_i\)采样自 \(\mathcal{U}[-1, 1]\)和\(\mathcal{U}[-5, 5]\)的结果. 我们希望输出\(f(x)\)是不平坦的, 但是也希望其不会偏向任意一些值, 显然采样自 \(\mathcal{U}[-5, 5]\)的较小的值占据了很大部分.

\(f(x)\)总共有\(H\)个结点, 满足

\[-1 < w_ix + b_i < 1, \]

的\(x\)区间为

\[-1/|w_i| - b_i/ w_i < x < 1 / |w_i| - b_i / w_i, \]

该区间长度为 \(2 / |w_i|\),
倘若不同结点

\[2 / |w_i| = 2 / H \rightarrow |w_i| = H. \]

即每个区间所对应的\(x\)的大小是一致的, 均为 \(2 / H\). 那么最后的输出也就很有可能是均匀的且并不完全平坦的.

注: 在这种情况下, 对于任意\(x \in [-1, 1]\), 只有一个区间 \(f_i(x)\)是落在\([-1, 1]\)的, 其余的都将表现出非线性, 从而导致不平坦?

为了让区间有所重叠, 实际上我们采用\(|w_i| = 0.7H\).

区间的中心 \(-b_i / w_i\)将从 \([-1, 1]\)从采样, 实际上

\[b_i \sim \mathcal{U}[-|w_i|, |w_i|]. \]

最后 \(v_i\) 均匀采样自 \(\mathcal{U}[-0.5, 0.5]\).

下面是几个示例:

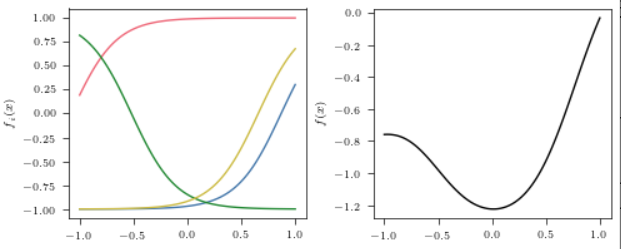
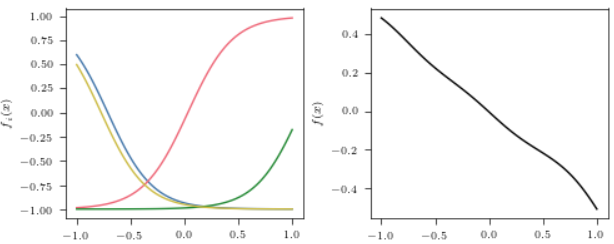
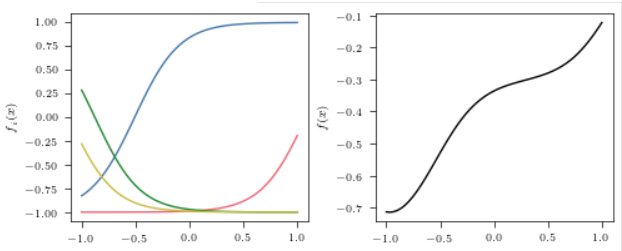
多维情形

作者给出的是从\(f_i(x)\)到其傅里叶变换表示的解释, 但是说实话
我不是很理解其中的具体思路 (可能是傅里叶变换了解得不是很透彻).
我这里勉强给个自己的解释吧.

首先,

\[f_i(\bm{x}) = v_i \tanh (\bm{w}_i^T \bm{x} + b_i). \]

倘若\(\bm{x} \in [-1, 1]^d\), 那么

\[-\|\bm{w}_i\|_1 + b_i \le \bm{w}_i^T\bm{x} + b_i \le \|\bm{w}_i\|_1 + b_i, \]

最大区间长度为\(2\|\bm{w}_i\|_1\). 和之前一维一样, 我们希望不同的区间长度是一致的, 即\(\|\bm{w}_i\|_1\)对于不同的\(i\)的大小也是一致的.

文中给出的是

\[\|\bm{w}\|_1 = H^{\frac{1}{d}}. \]

类似地, 在实际中, 采用

\[\|\bm{w}\|_1 = 0.7 * H^{\frac{1}{d}}. \]

并且, \(b_i\)采样自\(\mathcal{U}[-\|\bm{w}_i\|_1, \|\bm{w}_i\|_1]\).

注: 该系数是通过傅里叶变换, slices之类的推导出来的, 但是我没有搞清楚其中的关系;
注: 文中用的\(|\cdot|\)来表示大小, 我没法保证这就是\(\ell_1\)范数.

代码

import torch.nn as nn
import torch.nn.functional as F

def nguyen_widrow_init(weight, bias, scale: float = 0.7):
    out_channels, in_channels = weight.size()
    nn.init.uniform_(weight, -0.5, 0.5)
    scale = scale * out_channels ** (1 / in_channels)
    weight.data.copy_(scale * F.normalize(weight.data, p=1, dim=-1))
    nn.init.uniform_(bias, -scale, scale)

# test

import torch
import torch.nn as nn
import torch.nn.functional as F

from freeplot.base import FreePlot

class Net(nn.Module):

    def __init__(self) -> None:
        super().__init__()

        self.linear1 = nn.Linear(1, 4)
        self.linear2 = nn.Linear(4, 1)


        nguyen_widrow_init(self.linear1.weight, self.linear1.bias)
        nn.init.uniform_(self.linear2.weight, -0.5, 0.5)
        nn.init.uniform_(self.linear2.bias, -0.5, 0.5)

    def forward(self, x):
        z = torch.tanh(self.linear1(x))
        y = self.linear2(z)
        return z, y


model = Net()
x = torch.linspace(-1, 1, 100).view(-1, 1)
z, y = model(x)

x = x.flatten().detach().clone().numpy()
y = y.flatten().detach().clone().numpy()
z = z.transpose(0, 1).detach().clone().numpy()


fp = FreePlot((1, 2), (5, 2), sharey=False)
for i in range(4):
    fp.lineplot(x, z[i], label=str(i))
fp.lineplot(x, y, label='ALL', index=(0, 1), color='black')
fp.set_label(r"$f_i(x)$", index=(0, 0))
fp.set_label(r"$f(x)$", index=(0, 1))
fp.show()