Generative Modeling by Estimating Gradients of the Data Distribution

目录

• 概
• 主要内容
  • Langevin dynamics
  • Score Matching
  • Denoising Score Matching
  • Noise Conditional Score Networks
    • Slow mixing of Langevin dynamics
    • 损失函数
    • Annealed Langevin dynamics
    • 细节
• 代码

Song Y. and Ermon S. Generative modeling by estimating gradients of the data distribution. In Advances in Neural Information Processing Systems (NIPS), 2019.

概

当前生成模型, 要么依赖对抗损失(GAN), 要么依赖替代损失(VAE), 本文提出了基于score matching 训练, 以及利用annealed Langevin dynamics推断的模型, 思想非常有趣.

主要内容

Langevin dynamics

对于分布$p(x)$, 我们可以通过下列方式迭代生成

$$\tilde{x}_t = \tilde{x}_{t-1} + \frac{\epsilon}{2} \nabla_x \log p (\tilde{x}_{t-1}) + \sqrt{\epsilon} z_t,$$

其中$\tilde{x}_0 \sim \pi(x)$来自一个先验分布, $z_t \sim \mathcal{N}(0, I)$. 当步长$\epsilon \rightarrow 0$并且$T \rightarrow +\infty$的时候, $\tilde{x}_T$可以认为是从$p(x)$中采样的样本.

注: 一般的Langevin, dynamics还需要在每一次迭代后计算一个接受概率然后判断是否接受, 不过在实际中这一步往往可以省略.

Score Matching

通过上述的迭代可以发现, 我们只需要获得$\nabla_x \log p(x)$即可采样$x$, 我们可以期望通过下面的方式, 通过一个网络$s_{\theta}(x)$来逼近$\nabla_x \log p_{data}(x)$:

$$\min_{\theta} \: \frac{1}{2} \mathbb{E}_{p_{data}(x)} [\| s_{\theta} (x) - \nabla_x \log p_{data}(x) \|_2^2],$$

但是在实际中, 先验$\log p_{data}(x)$也是未知的, 幸运的是上述公式等价于:

$$\min_{\theta} \: \mathbb{E}_{p_{data}(x)} [\mathrm{tr}(\nabla_x s_{\theta} (x)) + \frac{1}{2} \|s_{\theta}(x)\|_2^2].$$

注: 见 score matching

Denoising Score Matching

一个共识是, 所获得的数据往往是一个低维流形, 即其内在的维度实际上很低. 所以$\mathbb{E}_{p_{data}(x)}$在实际中会出现高密度的区域估计得很好, 但是低密度得区域估计得非常差. Denosing Score Matching提高了一个较为鲁棒的替代方法:

$$\min_{\theta} \: \frac{1}{2} \mathbb{E}_{q_{\sigma}(\tilde{x}|x)p_{data}(x)} [\| s_{\theta} (\tilde{x}) - \nabla_x \log q_{\sigma}(\tilde{x}|x) \|_2^2].$$

当优化得足够好的时候,

$$s_{\theta^*}(x) = \nabla_x \log q_{\sigma}(x), \: q_{\sigma}(\tilde{x}) := \int q_{\sigma}(\tilde{x}|x) p_{data}(x) \mathrm{d}x.$$

实际中, 通常取$q_{\sigma}(\tilde{x}|x) = \mathcal{N}(\tilde{x}|x, \sigma^2 I)$, 相当于在真实数据$x$上加了一个扰动, 当扰动足够小($\sigma$足够小)的时候, $q_{\sigma}(x) \approx p_{data}(x)$, 则$s_{\theta^*}(x) \approx \nabla_x \log p_{data}(x)$.

注: 为啥期望部分要有$p_{data}$? 实际上上述目标和score matching依旧是等价的.

Noise Conditional Score Networks

Slow mixing of Langevin dynamics

假设$p_{data}(x) = \pi p_1(x) + (1 - \pi)p_2(x)$, 且$p_1, p_2$的支撑集合是互斥的, 那么 $\nabla_{x} \log p_{data}(x)$要么为$\nabla_{x} \log p_{1}(x)$或者$\nabla_{x} \log p_{2}(x)$, 与$\pi$没有丝毫关联, 这会导致训练的结果与$\pi$也没有关联. 在实际中, 若$p_1, p_2$近似互斥, 也会产生类似的情况:

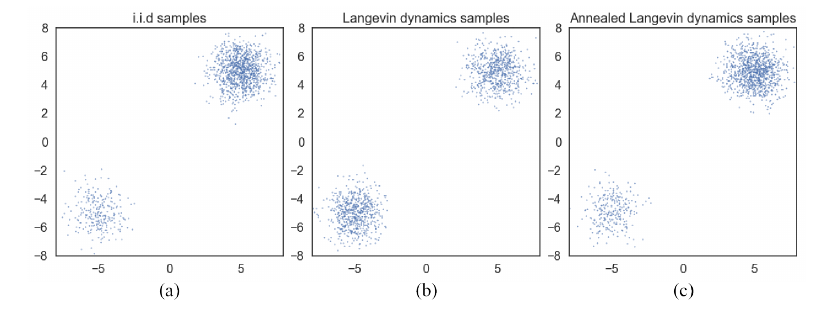
如上图所示, 通过Langevin dynamics采样的点几乎是1:1的, 这与真实的分布便有了出入.

作者的想法是, 设计一个noise conditional score networks:

$$s_\theta(x, \sigma),$$

给定不同的$\sigma$其拟合不同扰动大小的$p_{\sigma}$, 在采样中, 首先用大一点的$\sigma$, 然后再逐步缩小, 这便是一种退火的思想. 显然, 一开始用大一点的$\sigma$能够为后面的采样提供更好更鲁棒的初始点.

损失函数

设定$\sigma_i, i=1,2,\cdots, L$, 且满足:

$$\frac{\sigma_1}{\sigma_2} = \cdots = \frac{\sigma_{L-1}}{\sigma_L} > 1,$$

即一个等比例(缩小)的数列.
对于每个$\sigma$采用如下损失:

$$\ell(\theta; \sigma) = \frac{1}{2} \mathbb{E}_{p_{data}(x)} \mathbb{E}_{\mathcal{N}(\tilde{x}|x, \sigma I)} [\| s_{\theta} (\tilde{x}, \sigma) + \frac{\tilde{x} - x}{\sigma^2} \|_2^2].$$

注: $\nabla_{\tilde{x}} q_{\sigma}(\tilde{x}|x) = -\frac{\tilde{x} - x}{\sigma^2}$.

于是总损失为

$$\mathcal{L}(\theta; \{\sigma_i\}_{i=1}^L) := \frac{1}{L}\sum_{i=1}^L \lambda (\sigma_i)\ell(\theta;\sigma_i),$$

$\lambda(\sigma_i)$为权重系数.

Annealed Langevin dynamics

Input: $\{\sigma_i\}_{i=1}^L, \epsilon, T$;

1. 初始化$x_0$;
2. For $i=1,2,\cdots, L$ do:
   • $\alpha_i \leftarrow \epsilon \cdot \sigma_i^2 / \sigma_L^2$;
   • For $t=1,2,\cdots, T$ do:
     • 采样$z_t \sim \mathcal{N}(0, I)$;
     • $x_t \leftarrow x_{t-1} + \frac{\alpha_i}{2}s_{\theta}(x_{t-1}, \sigma) + \sqrt{\alpha_i} z_t$;
   • $x_0 \leftarrow x_T$;

Output: $x_T$.

细节

1. 关于参数$\lambda(\sigma)$的选择:
   作者推荐选择$\lambda(\sigma) = \sigma^2$, 因为当优化到最优的时候, $\|s_{\theta}(x, \sigma)\|_2 \propto 1 / \sigma$, 故$\sigma^2 \ell(\theta;\sigma) = \frac{1}{2}\mathbb{E}[\|\sigma s_{\theta}(x, \sigma) + \frac{\tilde{x} - x}{\sigma} \|_2^2]$, 其中$\sigma s_{\theta}(x, \sigma) \propto 1, \frac{\tilde{x} - x}{\sigma} \sim \mathcal{N}(0, I)$, 故$\sigma^2 \ell_{\theta,\sigma}$与$\sigma$无关.

2. 关于$\alpha_i \leftarrow \epsilon \cdot \sigma_i^2 / \sigma_L^2$:

对于一次Langevin dynamic, 其获得的信息为: $\frac{\alpha_i}{2} s_{\theta}(x_{t-1}, \sigma)$, 其噪声为$\sqrt{\alpha_i}z_t$, 故其信噪比(signal-to-noise)为(应该是element-wise的计算?)

$$\frac{\alpha_i s_{\theta}(x, \sigma_i)}{2 \sqrt{\alpha_i} z},$$

当我们按照算法中的取法时, 我们有

$$\begin{array}{ll} \|\frac{\alpha_i s_{\theta}(x, \sigma_i)}{2 \sqrt{\alpha_i} z}\|_2^2 &\approx\frac{\alpha_i \| s_{\theta}(x, \sigma_i)\|_2^2}{4} \\ &\propto\frac{\|\sigma_i s_{\theta}(x, \sigma_i)\|_2^2}{4} \\ &\propto \frac{1}{4}. \end{array}$$

故采用此策略能够保证SNR保持一个稳定的值.

代码

原文代码