HAT
概
本文认为普通的对抗训练会导致不必要的adversarial margin从而牺牲过多的精度.
于是提出一种Helper-based adversarial training (HAT)来帮助网络学习.
主要内容
作者认为, 一个样本\(\bm{x}\)沿着一个方向\(\hat{\bm{r}}\)的margin可以按照如下方式定义:
\[\mu(\bm{x}, \hat{\bm{r}}) = \arg\min_{\alpha} |\alpha |
\quad \mathrm{s.t.} \: F(\bm{x} + \alpha \hat{\bm{r}}) \not = F(\bm{x}),
\]
其中\(F(\bm{x}) = \arg\max_{k} f_k(\bm{x})\)为预测类别.
\(\bm{x}\)的对抗方向, 可以定义为:
\[\bm{r}_i = \frac{\delta}{\|\delta\|}, \: \delta = \max_{\|\delta\|\le \epsilon} \ell(y_i, f_{\theta} (\bm{x}_i + \delta)).
\]
某种意义上就是最短路径.
作者通过实验发现, 对抗训练会使得样本的对抗方向\(\bm{r}_i\)变得不必要得大, 这会导致自然精度的严重下降.
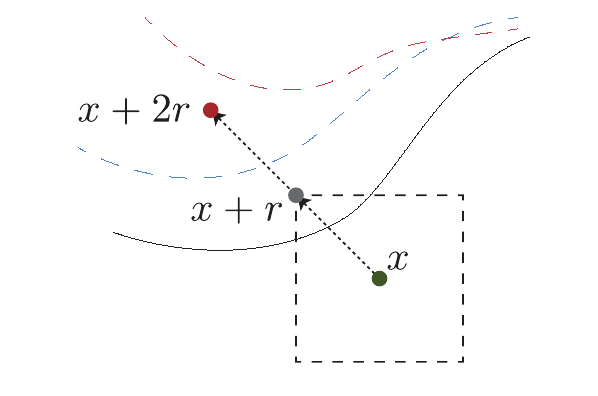
如下图所示, 其实蓝色的决策边界已经足够保证鲁棒性, 而对抗训练会使得决策边际变成红色. 所以作者通过\(\bm{x} + 2\bm{r}\)喂入普通网络得到一个预测标签\(\tilde{y}\), 利用这个来告诉对抗训练的网络, 其实这个margin不必这么大. 这相当于前后各限制了一个条件.
最后的算法如下:



