Morphological Image Processing

目录

• 概
  • reflection and translation
• Erosion and Dilation
  • Erosion
    • 示例
    • skimage.morphology.erosion
  • dilation
    • 示例
    • skimage.morphology.dilation
  • 对偶性
• Opening and Closing
  • Opening
    • 示例
    • skimage.morphology.opening
  • Closing
    • 示例
    • skimage.morphology.closing
  • 对偶性
• The Hit-or-Miss Transform
• 一些基本的操作
  • Boundary Extraction
  • Hole Filling
  • Extraction of Connected Components
  • Convex Hull
    • skimage.morphology.convex_hull_image
  • Thinning
    • skimage.morphology.thin
  • Thickening
  • Skeletons
    • skimage.morphology.skeletonize
    • Pruning
• Morphological Reconstruction
  • Geodesic Dilation and Erosion
  • Morphological Reconstruction by Dilation and by Erosion
  • Opening|Closing by Reconstruction
  • Automatic Algorithm for Filling Holes
  • Border Clearing

Gonzalez R. C. and Woods R. E. Digital Image Processing (Forth Edition)

符号	即	操作	说明
\(\ominus\)	erosion	\(\{z:(B)_z \subset A\}\)	Erodes the boundary of A
\(\oplus\)	dilation	\(\{z:(\hat{B})_z \bigcap A \not= \empty\}\)	Dilates the boundary of A
\(\circ\)	opening	\((A \ominus B) \oplus B\)	Smoothes contours, breaks narrow isthmuses, and eliminates small islands and sharp peaks.
\(\bullet\)	closing	\((A\oplus B) \ominus B\)	Smoothes contours, fuses narrow breaks and long thin gulfs, and eliminates small holes.
\(\circledast\)	hit-or-miss	\(\{z:(B)_z \subset I\}\)	Finds I. B contains instances both of foreground B in image and background elements.
\(\beta(A)\)	boundary extraction	\(A - (A \ominus B)\)	Set of points on the boundary of set A
-	hole filling	\((X_{k-1} \oplus B) \bigcap I^c\)	Fills holes in A
-	connected components	\((X_{k-1} \oplus B) \bigcap I\)	Finds connected components in \(I\).
\(C(A)\)	convex hull	\((X_{k-1}^i \circledast B^i) \bigcup X_{k-1}^i\)	Finds the convex hull
\(\otimes\)	thining	\(A - (A \circledast B)\)	Thins set A
\(\odot\)	thickening	\(A\bigcup (A \circledast B)\)	Thickens set A
\(S(A)\)	skeleton	$(A \ominus kB) - (A \ominus kB) \circ B $	Finds the skeleton of set A
-	pruning	...	\(X_4\) is the result of pruning set A.
\(D_G^{(1)}(F)\)	geodesic dilation	\((F \oplus B) \bigcap G\)	-
\(E_G^{(1)}(F)\)	geodesic erosion	\((F \ominus B) \bigcup G\)	-
\(R_G^D(F)\)	morphological reconstruction by dilation	\(R_G^D (F) = D^{(k)}_G (F)\)	-
\(R_G^E(F)\)	morphological reconstruction by erosion	\(R_G^E (F) = E^{(k)}_G (F)\)	-
\(O_R^{(n)}(F)\)	opening by reconstruction	\(R_{F}^D (F \ominus nB)\)	-
\(C_R^{(n)}(F)\)	closing by reconstruction	$ R_{F}^E (F \oplus nB)$	-
-	hole filling	$H = [R_{Ic}D(F)]^c $	Auto
-	border clearing	\(I - R_I^D(F)\)	-

概

直接把整个章节都拿来是决定这个形态学的东西实在是有趣, 加之前后联系过于紧密, 感觉如果过于割裂会导致以后回忆不起来, 所以直接对整个章节做个笔记得了.

我觉得首先需要牢记的是, 本章节是在集合的基础上讨论的, 对于一个二元图中的物体, 我们可以通过如下集合表示:

\[\{(x_1, y_1), \cdots, (x_N, y_N)\}, \]

\((x, y)\)表示值为\(1\)的坐标(这里假设foreground pixel的值为1, 当然也可以假设其为0).

注: 个人觉得, 这里讨论的时候并非像之前的图片一样以左上角原点, 而是以目标中心为原点然后发散开去(只是单纯便于理解和书写, 实际处理是不受影响的). 也就意味着, \(x, y\)是可以为负的, 显然这种表示的好处是不需要确定整个图片的大小范围.

本章节会频繁涉及到objects和structuring elements (SE)的概念, 说实话其具体的定义不是很清楚, 我还是从任务的角度来给它们做个解释.

因为本章节讨论的transform, 通常都是通过SE经过一些集合操作使得objects发生某种改变, 所以objects就是对象. SE

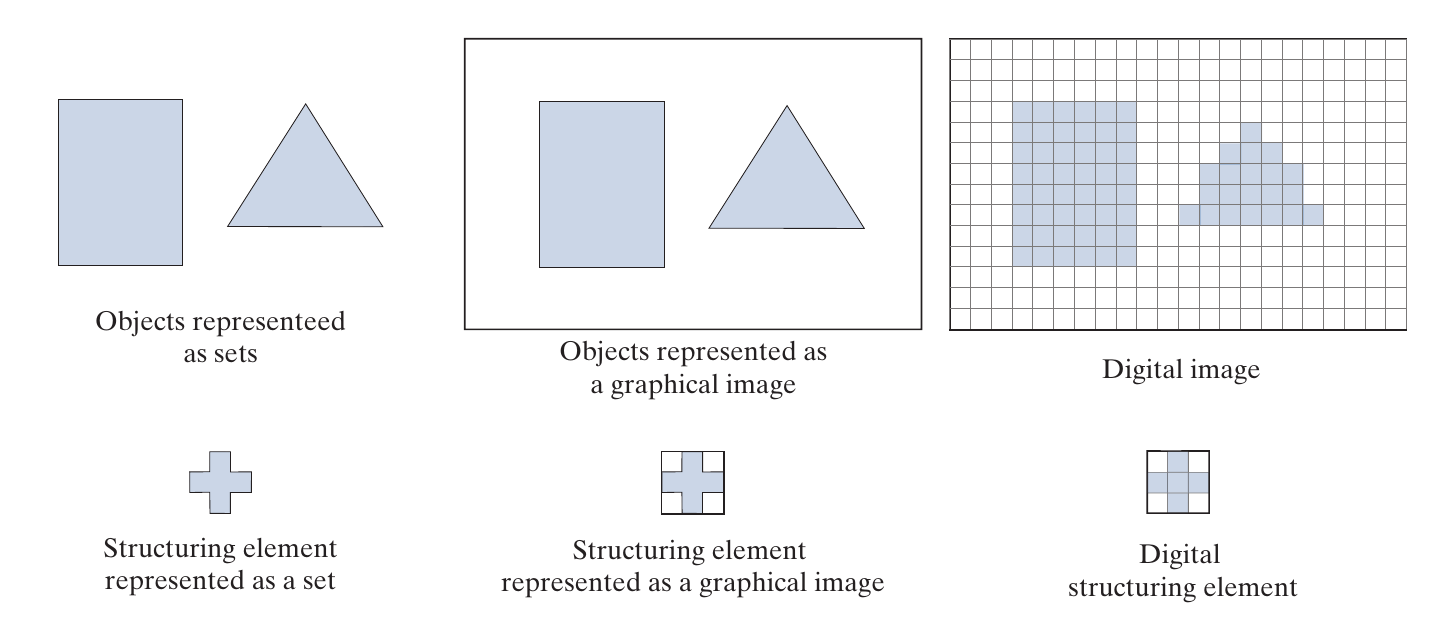
如上图所示, 虽然objects是一个仅仅记录0值的集合, 我们通常将其置于一个矩形区域中, 便于图片的处理, SE也是类似的. 特别的是, SE整体除了0, 1外还可能有\(\times\)的属性, 其表示0或1, 即该位置的点不我们所关心的点, 其可以任意匹配.

reflection and translation

反射, 即

\[\hat{B} = \{w| w=-b, \text{for } b \in B\}, \]

需要注意的是该反射是以\(B\)的中心为原点的.

平移, 即

\[(B)_z = \{c| c= b+z, \text{for } b \in B\}. \]

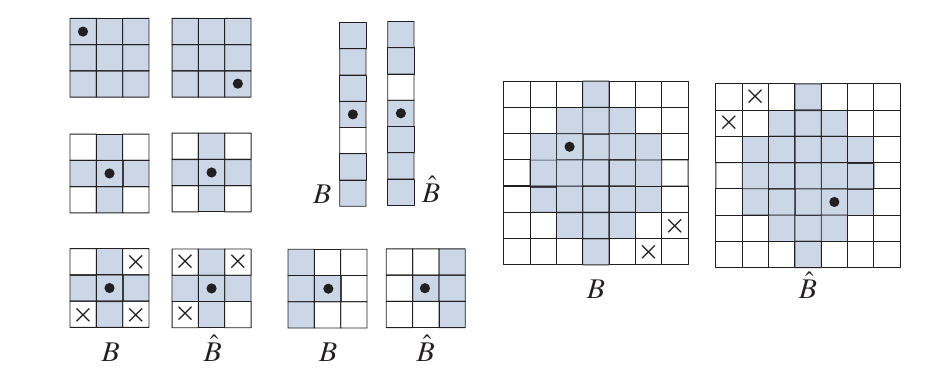
Erosion and Dilation

Erosion

Erosion操作能够令图片中的元素'缩小', 所以其在处理噪声的时候其实不错. 其定义为:

\[\begin{array}{ll} A \ominus B &= \{z| (B)_z \subset A\} \\ &= \{w \in Z^2 | w + b \in A \text{ for every } b \in B\} \\ &= \mathop{\bigcap} \limits_{b \in B} (A)_{-b}. \end{array} \]

proof:

设上面三个定义分别为\(C_1, C_2, C_3\).
\(C_1 \subset C_2\):

\(\forall z \in C_1\),

\[\{b_1+z, b_2 + z, \cdots\} \subset A, \]

故

\[z + b \in A, \text{ for every } b \in B \Rightarrow C_1 \subset C_2. \]

\(C_2 = C_3\):

\[C_2 = \{w \in Z^2 | w + b \in A \text{ for every } b \in B\} =\bigcap_{b \in B} \{a-b \in Z^2 | \in A\} =\bigcap_{b \in B} (A)_{-b}. \]

\(C_3 \subset C_1\):

\(\forall w \in C_2\):

\[(B)_w \subset A \Rightarrow C_3 \subset C_1. \]

示例

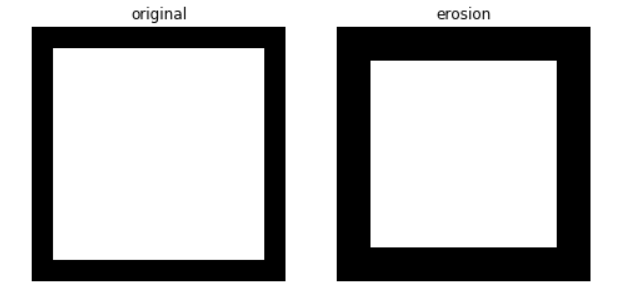
如下图所示, 第一行第一幅图是object, 通过第二幅SE erosion后object缩小了, 而通过第二行的SE更是直接成了一条线.

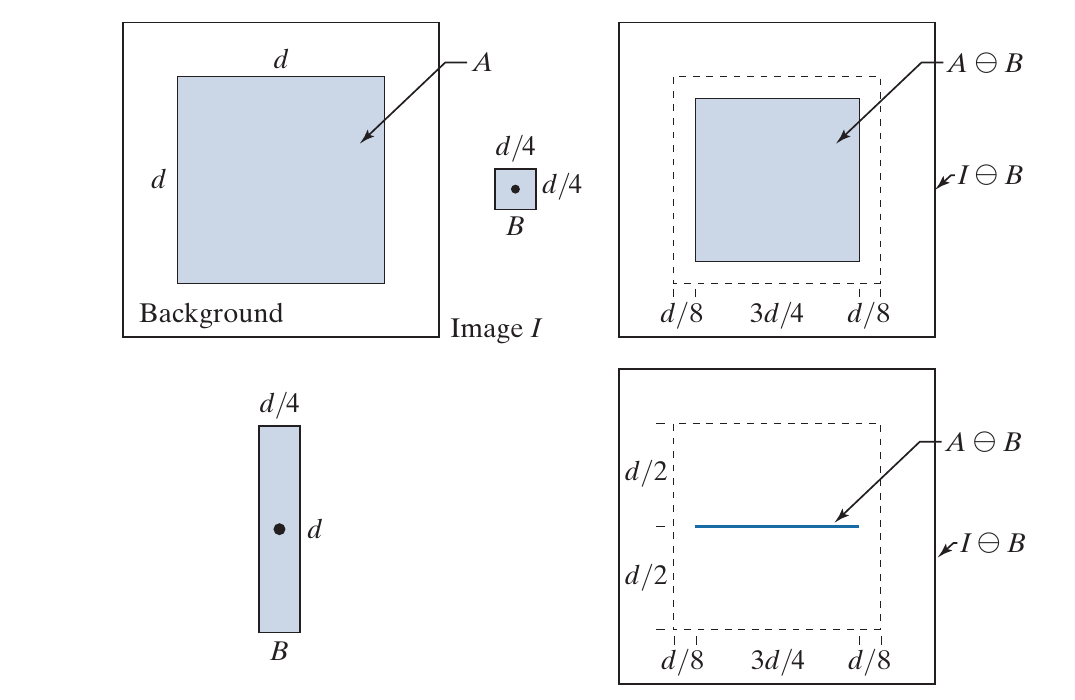
skimage.morphology.erosion

[erosion](Module: morphology — skimage v0.19.0.dev0 docs (scikit-image.org))

import numpy as np
import matplotlib.pyplot as plt
from skimage.morphology import erosion, disk

def plot_comparison(original, filtered, filter_name):

    fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(8, 4), sharex=True,
                                   sharey=True)
    ax1.imshow(original, cmap=plt.cm.gray)
    ax1.set_title('original')
    ax1.axis('off')
    ax2.imshow(filtered, cmap=plt.cm.gray)
    ax2.set_title(filter_name)
    ax2.axis('off')

img = np.ones((100, 100))
arow = np.zeros((10, 100))
img = np.vstack((arow, img, arow))
acol = np.zeros((120, 10))
img = np.hstack((acol, img, acol)).astype(np.uint8)
fig, ax = plt.subplots()
ax.imshow(img, cmap=plt.cm.gray)

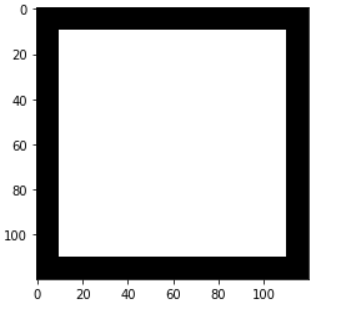
footprint = disk(6) # {0, 1}, 半径为6的圆, 中心元素为1其余为0
eroded = erosion(img, footprint)
plot_comparison(img, eroded, 'erosion')

dilation

dilation的效果是令图中的元素进行扩张, 一些扫描的文本图像可能字符剑有断痕, 通过此可以修复.

其集合定义为:

\[\begin{array}{ll} A \oplus B &= \{z| (\hat{B})_z \bigcap A \not= \empty\} \\ &= \{w \in Z^2| w = a+ b, \text{ for some } a \in A \text{ and } b \in B\}\\ &= \mathop{\bigcup}_{b \in B} (A)_b \\ &= \mathop{\bigcup}_{a \in A} (B)_a. \end{array} \]

proof:

记上面四种定义各自为\(C_1, C_2, C_3, C_4\):

\(C_1 = C_2\):

\(\forall z \in C_1\):

\[\exist a \in A, b \in B, \quad \mathrm{s.t.} \: -b + z = a \rightarrow z = a + b \rightarrow z \in C_2, \]

故

\[C_1 \subset C_2. \]

\(\forall w \in C_2\):

\[\exist a \in A, b \in B, \quad \mathrm{s.t.} \: w = a+b \rightarrow -b + w = a \rightarrow (\hat{B})_w \bigcap A \not= \empty, \]

故

\[C_2 \subset C_1. \]

\(C_2 = C_3 = C_4\):

显然.

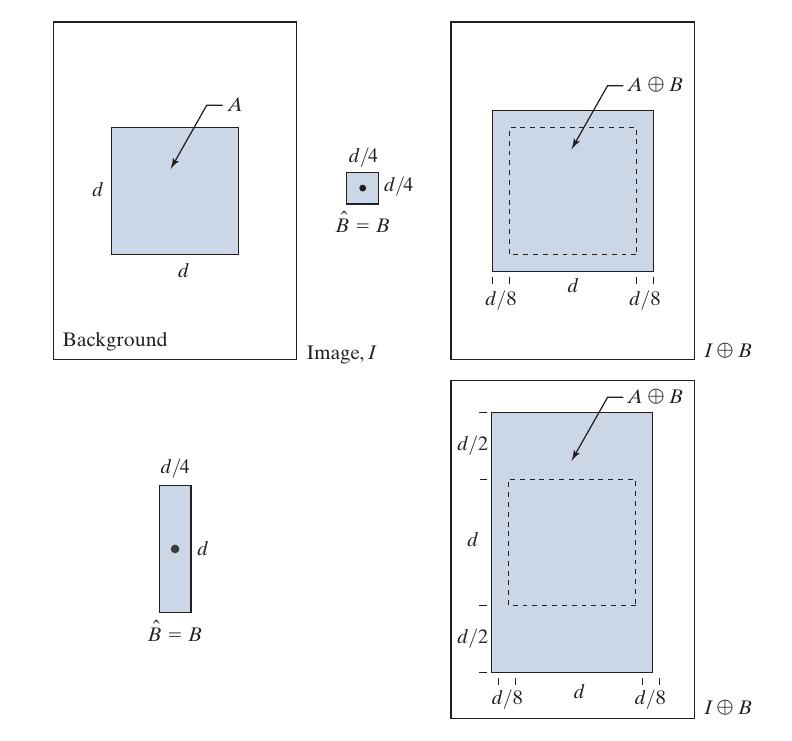
最后两个定义是很直观的, \(C_3\)相当于对于每一个点\(b\in B\)为中心画一个\(A\), \(C_4\)则是以每一个\(a \in A\)为中心画一个\(B\).

示例

skimage.morphology.dilation

dilation

from skimage.morphology import dilation
footprint = disk(6) # {0, 1}, 半径为6的圆, 中心元素为1其余为0
dilated = dilation(eroded, footprint)
plot_comparison(eroded, dilated, 'dilation')

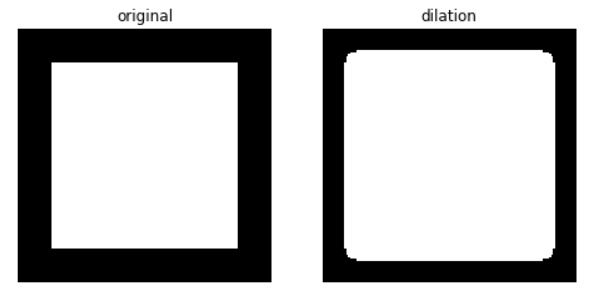
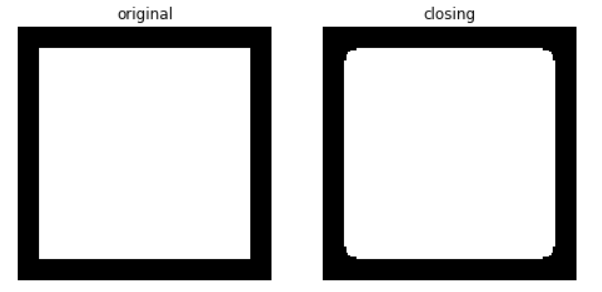
注: 圆角实际上是下一节的东西.

对偶性

\[\begin{array}{ll} (A\ominus B)^c &= \{z| (B)_z \subset A\}^c \\ &= \{z| (B)_z \bigcap A^c \not = \empty\} \\ &= A^c \oplus \hat{B}. \end{array} \]

\[\begin{array}{ll} (A\oplus B)^c &= \{z| (\hat{B})_z \bigcap A \not= \empty \}^c \\ &= \{z| (\hat{B})_z \subset A^c\} \\ &= A^c \ominus \hat{B}. \end{array} \]

Opening and Closing

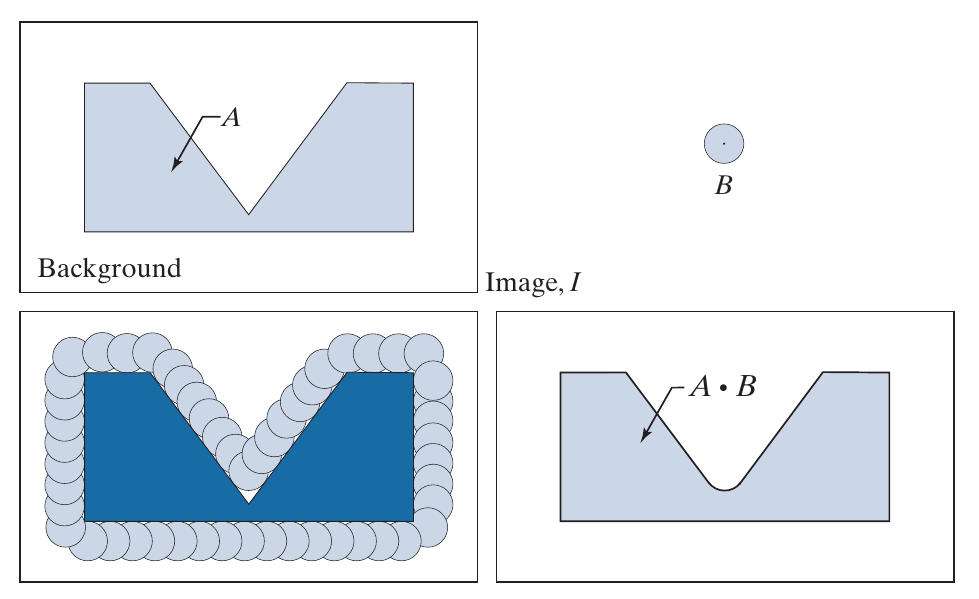
二者都有一种将目标变圆滑的效果.

Opening

定义:

\[A \circ B = (A \ominus B) \oplus B = \mathop{\bigcup} \limits_{z} \{(B)_z | (B)_z \subset A\}. \]

proof:

\[\begin{array}{ll} (A \ominus B) \oplus B &= \bigcup_{z \in A \ominus B} (B)_z \\ &= \bigcup_{z} \{(B)_z| (B)_z \subset A\}. \end{array} \]

示例

skimage.morphology.opening

opening

from skimage.morphology import opening
footprint = disk(6)
opened = opening(img, footprint)
plot_comparison(img, opened, 'opening')

Closing

定义:

\[A \bullet B = (A \oplus B) \ominus B = [\bigcup \{(\hat{B})_z| (\hat{B})_z \bigcap A = \empty\}]^c. \]

注: 书中为:

\[A \bullet B = (A \oplus B) \ominus B = [\bigcup \{(B)_z| (B)_z \bigcap A = \empty\}]^c, \]

但感觉不一样啊.

proof:

\[\begin{array}{ll} [(A \oplus B) \ominus B]^c &= (A \oplus B)^c \oplus \hat{B} \\ &= (A^c \ominus \hat{B}) \oplus \hat{B} \\ &= \bigcup_z \{(\hat{B})_z | (\hat{B})_z \subset A^c\} \\ &= \bigcup_z \{(\hat{B})_z | (\hat{B})_z \bigcap A = \empty\} \\ \end{array} \]

示例

skimage.morphology.closing

closing

from skimage.morphology import closing
footprint = disk(6)
closed = opening(img, footprint)
plot_comparison(img, closed, 'closing')

对偶性

\[(A \circ B)^c = (A^c \bullet \hat{B}) \\ (A \bullet B)^c = (A^c \circ \hat{B}) \]

且

\[(A \circ B) \circ B = A \circ B \\ (A \bullet B) \bullet B = A \bullet B. \]

The Hit-or-Miss Transform

主要用于shape detection.

定义:

\[I \circledast B_{1,2} = (A \ominus B_1) \bigcap (A^c \ominus B_2), \]

此为\(B_1, B_2\)不包含\(0\)元素的情形, 倘若允许\(B\)包含0元素, 那么

\[I \circledast B = I \ominus B, \]

只是我们\(B\)通常需要一些特殊的性质来使其具有detection的作用.

具体怎么shape detection 还是请回看原文吧.

一些基本的操作

Boundary Extraction

定义:

\[\beta(A) = A - (A \ominus B) \]

直观的感觉就是把object的中间部分挖掉.

Hole Filling

假设在我们想填的hole中已知一个点, 以这个点为基础出发(记为\(X_0\)):

\[X_k = (X_{k-1} \oplus B) \bigcap I^c, k=1,2,3,\cdots, \]

停止准则为

\[X_k = X_{k+1}. \]

不过需要注意的是, \(B\)应该选择下面类型的(如果是全满的话可能跳出hole了).

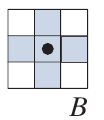
Extraction of Connected Components

抓取连通区域, 假设已知在我们想抓取的连通区域的一点, 从这个点出发(记为\(X_0\)):

\[X_k = (X_{k-1} \oplus B) \bigcap I, k=1,2,\cdots, \]

直到

\[X_{k+1} = X_k. \]

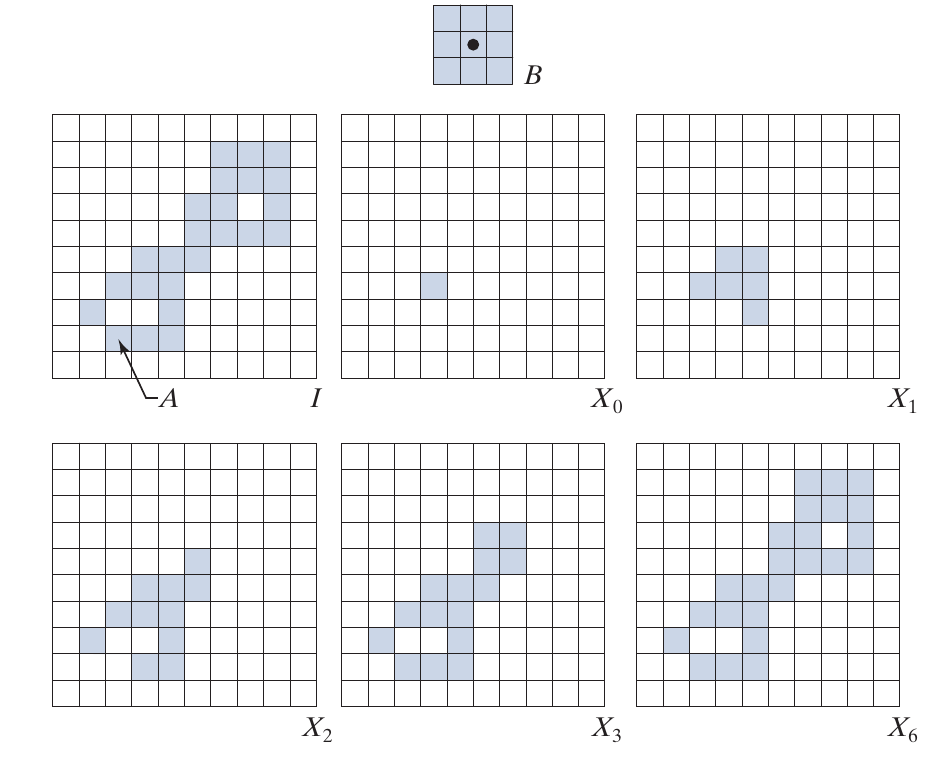
Convex Hull

将一个object填补成凸的, 这个说实话没怎么看明白.

\[X_k^i = (X_{k-1}^i \circledast B^i) \bigcup X_{k-1}^i, i=1,2,3,4, k=1,2,\cdots \\ X_0^i = I. \]

当

\[X_{k+1}^i = X_{k}^i \]

时停止, 记其为\(D^i\), 最后的convex hull 为

\[C(A) = \mathop{\bigcup}_{i=1}^4 D^i. \]

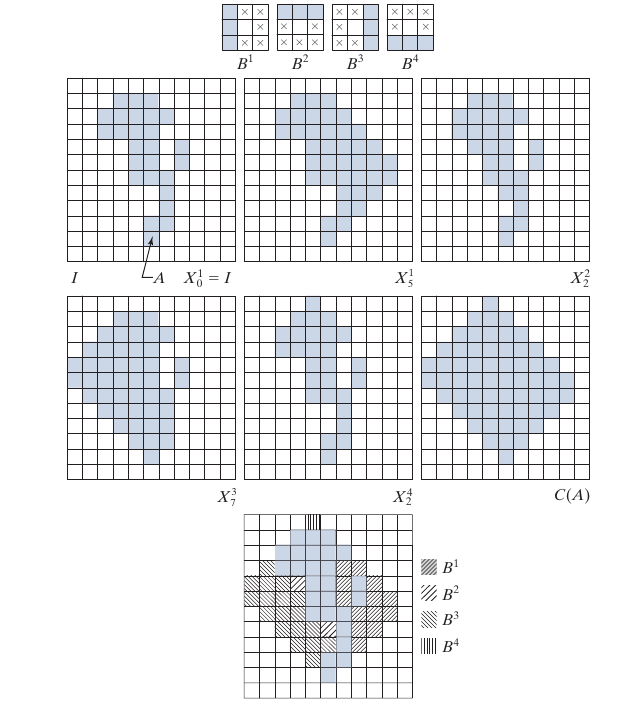
总感觉这个不是最小的凸包啊.

skimage.morphology.convex_hull_image

convex_hull

Thinning

定义:

\[A \otimes B = A - (A \circledast B) = A \bigcap (A \circledast B)^c \]

skimage.morphology.thin

thin

Thickening

相反的操作:

\[A \odot B = A \bigcup (A \circledast B). \]

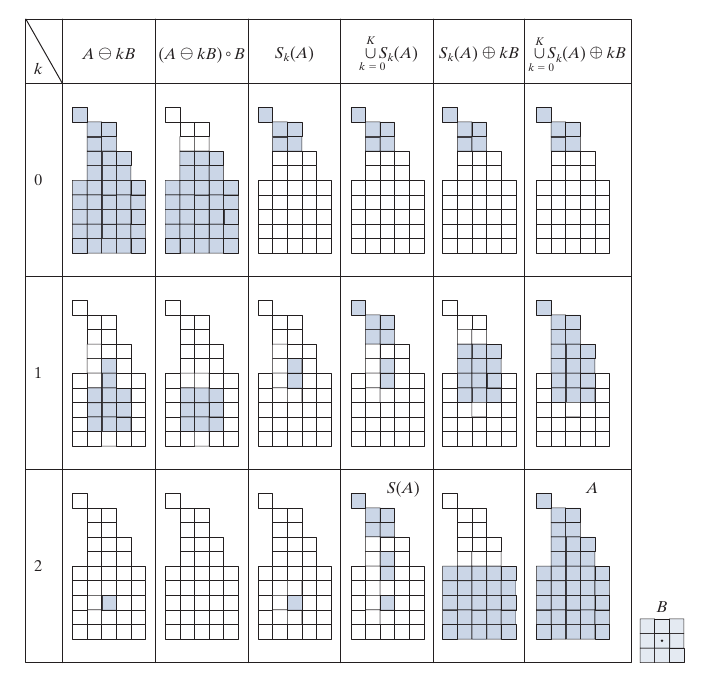
Skeletons

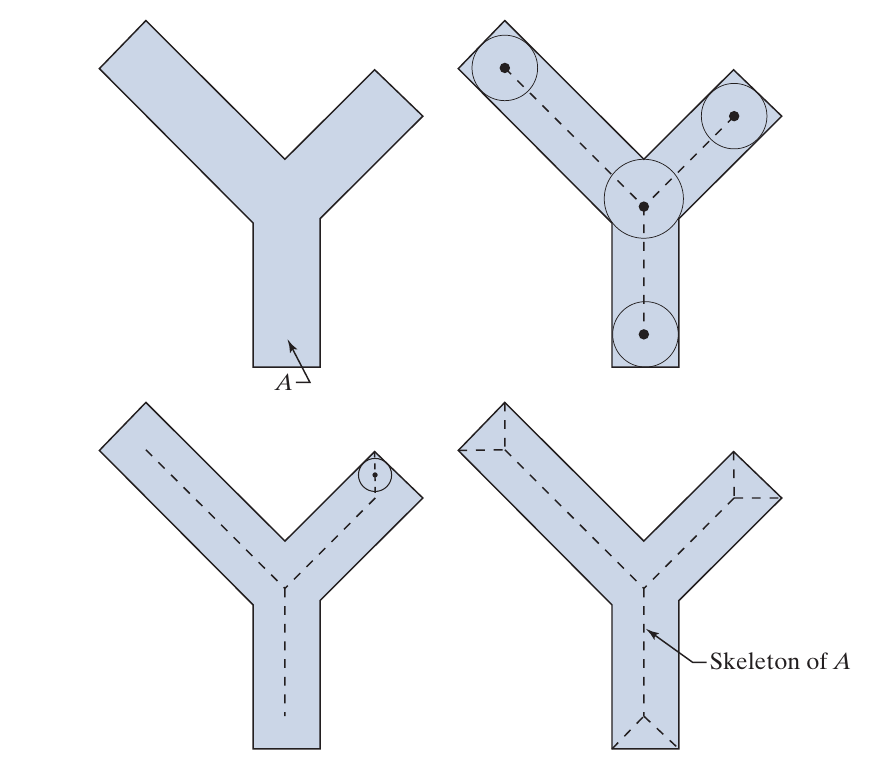
其严格的定义有些复杂, 感觉有点拓扑结构?

\[S(A) = \mathop{\bigcup} \limits_{k=0}^K S_k(A), \\ S_k(A) = (A \ominus kB) - (A \ominus kB) \circ B \\ (A \ominus kB) = ((\ldots ((A\ominus B) \ominus B)\ominus \ldots) \ominus B)\\ K = \max \{k| (A \ominus kB) \not = \empty \}. \]

skimage.morphology.skeletonize

skeleton

Pruning

pruning 方法用于去掉别的方法留下的一些spurs:

\[X_1 = A \otimes \{B\} \\ X_2 = \mathop{\bigcup} \limits_{k=1}^8 (X_1 \circledast B^k) \\ X_3 = (X_2 \oplus H) \bigcap A \\ X_4 = X_1 \bigcup X_3. \]

\(B^k\)为下图的一系列(而\(\{B\}\)为其中一部分不一定全部用到):

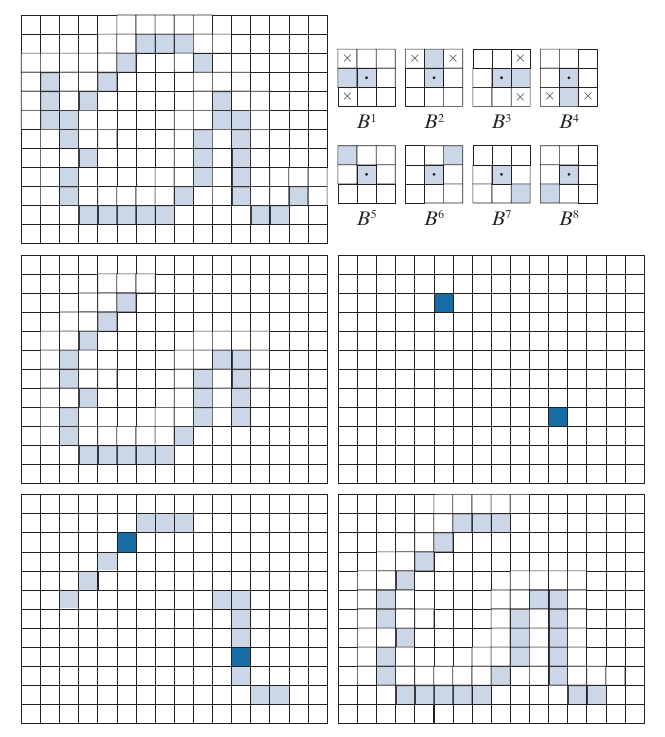
Morphological Reconstruction

Morphological Reconstruction除了之前用到的\(F, B\)外, 还要额外用到一个图片(称为mask)作为一个reconstruction的limit.

Geodesic Dilation and Erosion

假设\(F \subset G\), geodesic dilation:

\[D_G^{(1)} (F) = (F \oplus B) \bigcap G \\ D_G^{(n)} (F) = D_G^{(1)} (D_G^{(n-1)} (F)), \quad D_G^{(0)} (F) = F. \]

geodesic erosion:

\[E_G^{(1)}(F) = (F \ominus B) \bigcup G \\ E_G^{(n)}(F) = E_G^{(1)}(E_G^{(n-1)}(F)), \quad E_G^{(0)}(F) = F. \]

直观上很好解释, 即geodesic dilation在扩张的时候不能超过\(G\), 而geodesic erosion在收缩的时候不会少于\(G\).

Morphological Reconstruction by Dilation and by Erosion

定义很简单, 即重复上述操作直到收敛:

\[R_G^D (F) = D^{(k)}_G (F), \quad \text{if } D^{(k)}_G (F) = D^{(k-1)}_G (F), \\ R_G^E (F) = E^{(k)}_G (F), \quad \text{if } E^{(k)}_G (F) = E^{(k-1)}_G (F). \]

Opening|Closing by Reconstruction

\[O_R^{(n)}(F) = R_{F}^D (F \ominus nB), \]

直观解释就是, 先erosion \(n\)次, 再在此基础上不断扩张(受限于\(F\)).

Closing by Reconstruction 就是:

\[C_R^{(n)}(F) = R_{F}^E (F \oplus nB). \]

Automatic Algorithm for Filling Holes

之前介绍的hole filling需要一个点为基础, 这个算法是全自动的.

\[F(x, y) = \left \{ \begin{array}{ll} 1 - I(x, y) & \text{if } (x, y) \text{ is on the border of } I \\ 0 & \text{otherwise}. \end{array} \right . \]

\[H = [R_{I^c}^D(F)]^c \\ H \bigcap I^c \]

感觉还是挺好理解的, 就是从边边, 由于中间部分的hole一定会被包围起来, 所以\(H^c\)一定不包含中间部分的hole.

Border Clearing

\[F(x, y) = \left \{ \begin{array}{ll} I(x, y) & \text{if } (x, y) \text{ is on the border of } I \\ 0 & \text{otherwise}. \end{array} \right . \]

\[X = I - R_{I}^D(F). \]

能够把边缘的一些部分给去了.