Improving Adversarial Robustness via Channel-Wise Activation Suppressing
概
这两篇论文发现natural和adversarial样本在激活层的大小和分布有显著的不同.
主要内容
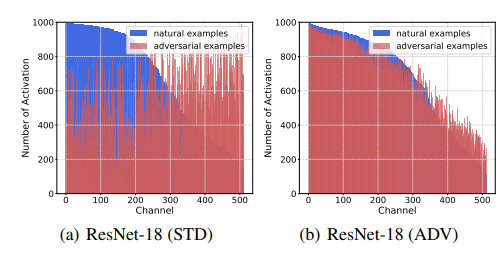
如上两图所示, 对抗样本的magnitude相较于干净样本要普遍大一些, 重要性的分布相较于干净分布更趋于均匀分布.
所以可以认为, 倘若我们能够恢复正常的大小以及回归正常的重要性指标, 那么就能够提高网络鲁棒性.
注: 上面的重要性分布是这么计算的: 对于固定的类, 计算每个channel对于判别为该类的贡献度是否超越一个阈值, 以统计的综合频率为最后的重要性.
对于每一个block (比如resnet中的block), 在最后的输出部分辅以重加权, 使得重要的激活层能够更加突出.
重加权是通过新的全连接层实现的, 假设特征图大小为
\[f^l \in \mathbb{R}^{H \times W \times K},
\]
其中\(K\)为channels的数目, 首先通过GAP得到:
\[\hat{f}_k^l = \frac{1}{H \times W} \sum_i \sum_j f_k^l (i, j).
\]
再通过全连接层\(M^l = [M_1^l, \cdots, M_C^l] \in \mathbb{R}^{K \times C}\)重加权
\[\tilde{f}^l =
\left \{
\begin{array}{ll}
f^l \otimes M_y^l, & \text{training}, \\
f^l \otimes M_{\hat{y}}^l, & \text{test}.
\end{array}
\right .
\]
其中训练时, \(y\)就是样本标签, 而测试时,
\[\hat{y} = \arg \max_i \hat{f}^TM_i,
\]
即预测值.
所以, 显然为了让\(M_y\)能够与样本标签紧密联系, 在训练的时候, 需要额外最小化一个交叉熵损失:
\[\mathcal{L}_{CAS}(p(x',\theta,M), y) = -\log p_y(x').
\]
这里\(x'\)表示对抗样本.
CIFS的思路是类似的, 这里不多赘述了.
