Attention Is All You Need
概
Transformer.
主要内容
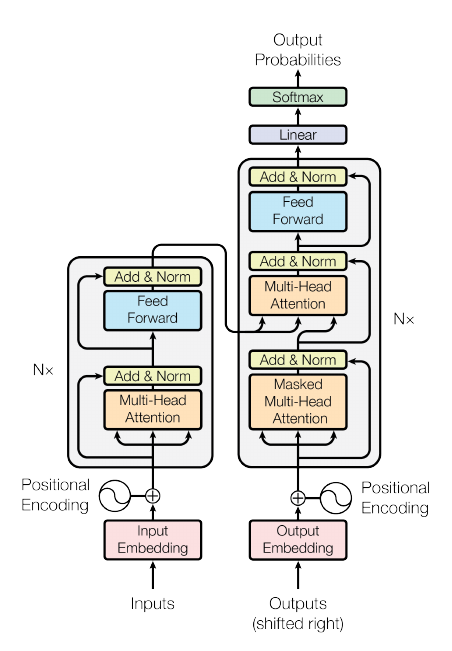
流程:
-
输出词句(source tokens)\(\mathbb{R}^S\), 通过字典(nn.Embedding)得到相应的embeddings:
\[x_i \in \mathbb{R}^D, i=1\cdots, S, \]由于是按照batch来计算的, 故整个可以输入可以有下列表示:
\[X \in \mathbb{R}^{B\times S \times D}. \]注: pytorch里输入是(S, B, D).
-
纯粹的attention不具备捕捉输入顺序的功能, 所以引入position embeddings:
\[p_{i, 2j} = \sin (i / 10000^{2j/D}), \: p_{i, 2j+1} = \cos (i / 10000^{2j/D}). \]\[x_i = x_i + p_i. \] -
encoder部分, 总共有N个, 每个进行如下的操作:
multi-attention: 首先, 定义权重矩阵\(W^Q, W^K, W^V \in \mathbb{R}^{D\times D}\),
\[Q = XW^Q, \\ K = XW^K, \\ V = XW^V, \]注: 这里的都是按batch的矩阵乘法(torch.matmul).
接下来变形(假设有\(H\)个heads)
\[(B, S, D) \rightarrow (B, S, H \times D/H) \rightarrow (B, H, S, D/H). \]此时\(Q, K, V\in \mathbb{R}^{B\times H \times S \times D/H}\).
接下来计算scores,
\[Z = QK^T \in \mathbb{R}^{B\times H \times S \times S}, \]注: 这里的\(K^T\)实际上是key.transpose(-2, -1), 此矩阵乘法是按照最后两个维度进行的(torch.matmul(Q, K.transpose(-2, -1))).
接下来对dim=-1进行softmax:
\[Z =\mathrm{Softmax}(\frac{Z}{\sqrt{D/H}}), \]一般的代码实现中是:
\[Z = \mathrm{Dropout}(\mathrm{Softmax}(\frac{Z}{\sqrt{D/H}})), \]计算最后的结果
\[Z = Z V, \]依旧是torch.matmul(Z, V)的意思, 再转成\(Z \in \mathbb{R}^{B \times S \times D}\), 最后outer projection, 根据\(W^{D \times D}\),
\[Z = ZW, \]最后有个残差连接:
\[X = \mathrm{LayerNorm}(X + Z), \]依旧实际中采用
\[X = \mathrm{LayerNorm}(X + \mathrm{Dropout}(Z)). \]feed forward: 这部分就是简单的:
\[X = \mathrm{LayerNorm}(X + \mathrm{ReLU}(XW_1 + b_1) W_2 + b2), \]在实际中加入dropout:
\[X = \mathrm{LayerNorm}(X + \mathrm{Dropout}[\mathrm{Dropout}[\mathrm{ReLU}(XW_1 + b_1)] W_2 + b2]). \] -
decoder部分, 同样由N个部件组成, 每个部件由self-attention, multi-attention 和 feed forward三部分组成, self-attention 和 feed forward 就是上面介绍的, multi-attention部分出入主要在于:
\[Q = YW^Q, \\ K = XW^K, \\ V = XW^V, \]这里用\(Y \in \mathbb{R}^{B \times T \times D}\)指代target embeddings. 需要注意的\(T, S\)即tokens的数量不一定一致, 但是矩阵乘法部分是没有问题的.
-
output probabilities, 输出最后的概率:
\[P = \mathrm{softmax}(VW) \in \mathbb{R}^{B \times T \times N_{voc}}, \]这里\(N_{voc}\)是字典的长度.
一个很重要的问题是, source, target是什么? 这篇博文讲得很清楚, 这里复述一下. 举个例子, 翻译任务, "You are welcome." -> "Da nada" 英语翻译成西班牙语, 那么 source = ['You', 'are', 'welcome', 'pad'], target = ['start', 'Da', 'nada', 'pad'], 预测的目标就是['Da', 'nada'].
在inference的时候, 是没有target的, 故流程如下:
- source = ['You', 'are', 'welcome', 'pad']通过encoder转成特征表示\(f\)用于重复利用;
- target = ['start', 'pad'], 输入decoder, 配合\(f\)得到预测, 取第一个预测'Da'(假设如此);
- 将其加入target = ['start', 'Da', 'pad'], 重复2, 得到预测['Da', 'nada'].
- 倘若还有后续, 便是重复上面的过程, 这是一种greedy的搜索方式.
问题: 那么为什么训练的时候不采取这种方式呢? 上面提到的那篇博文中, 提到这么做会导致训练困难且冗长, 但是我的感觉是, 这篇文章采取的是auto-agressive的逻辑, 所以每一个预测仅与它之前的词有关, 所以当已知target的时候, 重复上面的操作等价于直接传入整个target的预测. 因为在inference的时候, 只能一个一个来, 故比较恶心. 下面贴个上面博文的流程图, 感觉会清楚不少.
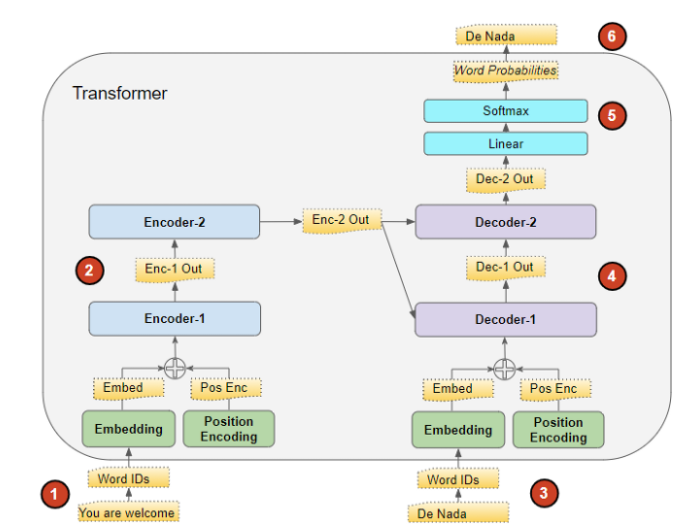
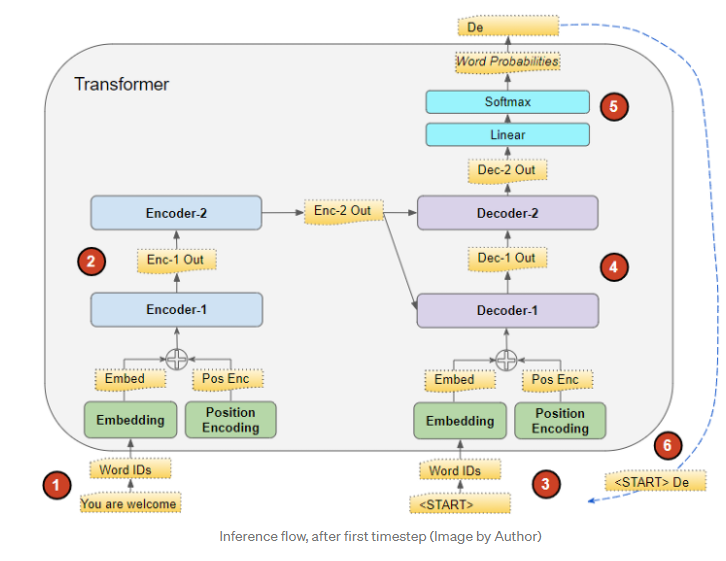
下面给出一些分析(多半是看别人的)
Positional Encoding
auto_regressive
注意到文章中有这么一句话:
At each step the model is auto-regressive [10], consuming the previously generated symbols as additional input when generating the next.
在代码中是通过mask实现的, 假设\(p\)代表scores, 一般来说attention的输出就是
此时是不满足auto-regressive, 为了保证\(o\)仅与\(V_1, \cdots, v_i\)有关(假设此为第i个token), 只需
若
只需
这里\(m\)即为mask.
实际上, 代码中还出现了pad_mask, 估计是tokens除了词以外还有别的类别和标签之类的符号, 这些不用于value部分就加上了.
当然mask是非强制性的.
额外的细节
注意到下面给出的代码中, 用于训练的标签smoothing的, 这个直觉上是对的, 毕竟替代词应该是不少的, 严格的one-hot不是好的主意.
代码
Pytorch 1.8 版本是有Transformer的实现的, 就是比较复杂, 感觉还是配合下面的比较容易理解:


