Noise
motivation
提高网络的一个有用的技巧就是增加训练数据: 真实数据, 或者用GAN拟合的数据.
这里想要研究的是, 噪声是否能够算作这类数据. 以CIFAR-10为例, 令
\[f: x \in \mathcal{X} \rightarrow p \in \mathbb{R}^{11},
\]
即除了原先的10类外, 额外增加一类为噪声类. 类似的思想好像在检测领域有用过(背景信息)?
本文的损失函数可以说是:
\[\min_f \quad \alpha \cdot \mathbb{E}_{x\sim \mathcal{D}} [\mathcal{L}(f(x+\delta_x), y)] + (1 - \alpha) \cdot \mathbb{E}_{z\sim P} [\mathcal{L} (f(z + \delta_z), 10)].
\]
其中\(x+\delta_x, z+\delta_z\)分别是真实数据\(x\)和噪声\(z\)的对抗样本, \(y \in \{0, 1, 2, \cdots, 9\}\).
个人觉得, 如果二者用同一个batch normalization, 那么滑动平均会非常振荡, 故额外考虑group normalization 和 让给干净样本分配一个BN, 噪声样本一个BN.
settings
- batch_size: 64
- beta1: 0.9
- beta2: 0.999
- dataset: cifar10
- description: AT=bn=64-0.5=default-sgd-0.1=pgd-linf-0.0314-0.25-10=64=default
- epochs: 200
- epsilon: 0.03137254901960784
- learning_policy: [100, 150]
- leverage: 0.5
- loss: cross_entropy
- lr: 0.1
- model: resnet18
- momentum: 0.9
- noise_batch_size: 64
- norm_layer: bn
- optimizer: sgd
- progress: False
- resume: False
- seed: 1
- steps: 10
- stepsize: 0.25
- transform: default
- weight_decay: 0.0005
results
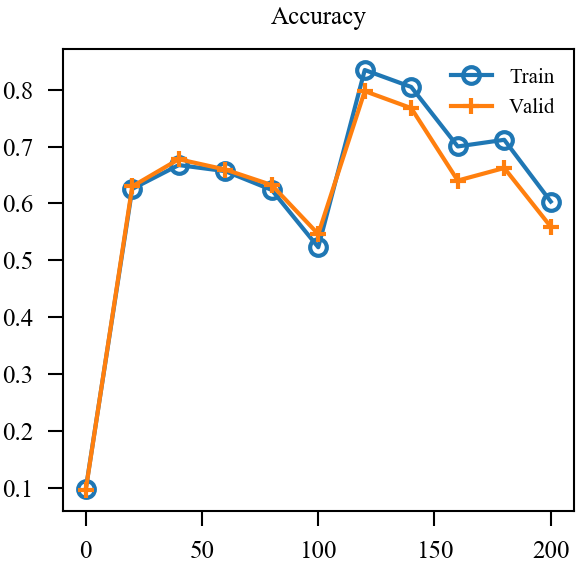
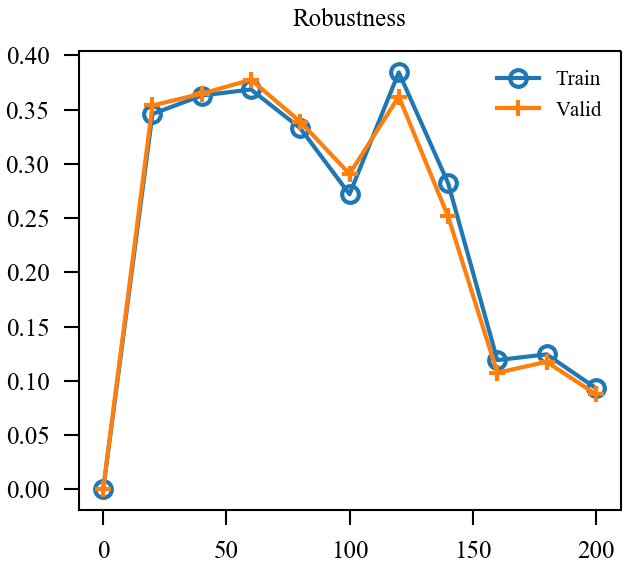
| Loss | Accuracy | Robustness | |
|---|---|---|---|
| BN |  |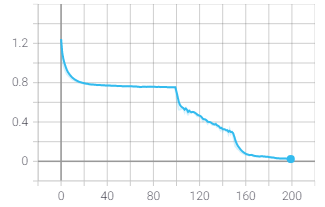
 |
 |
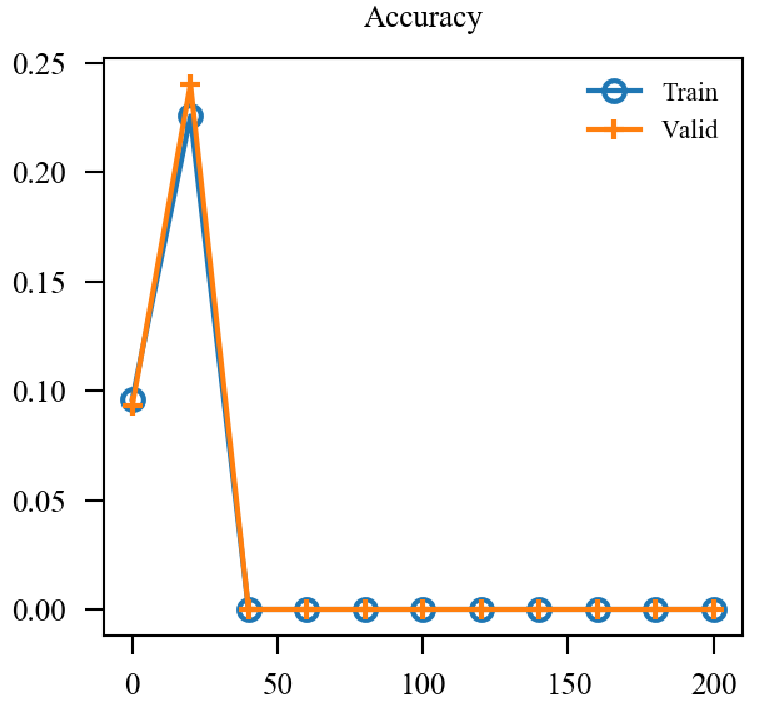
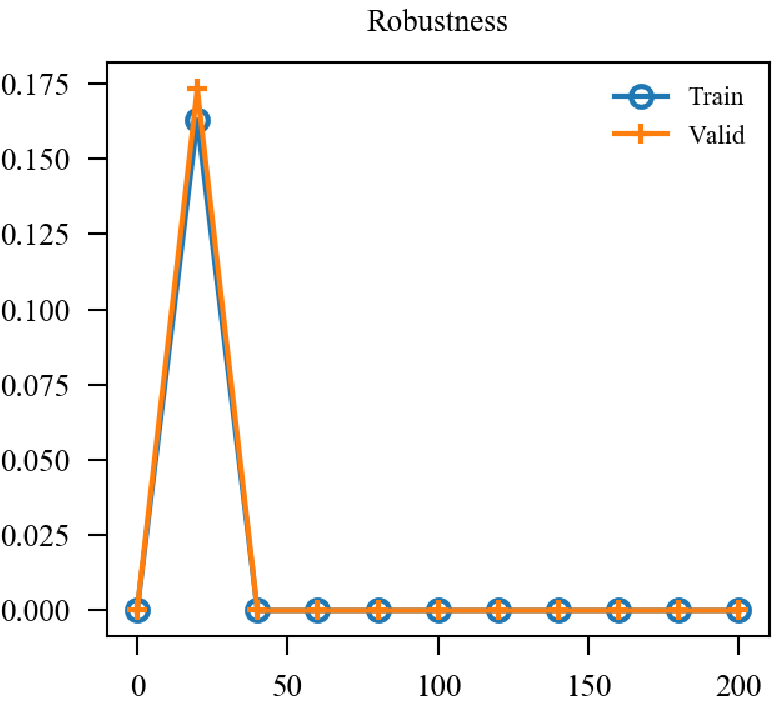
| GN |  |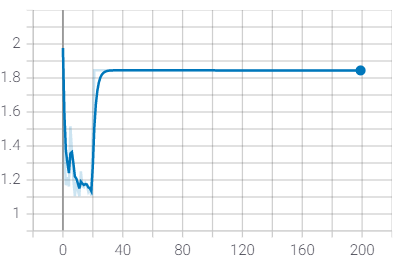
 |
 |
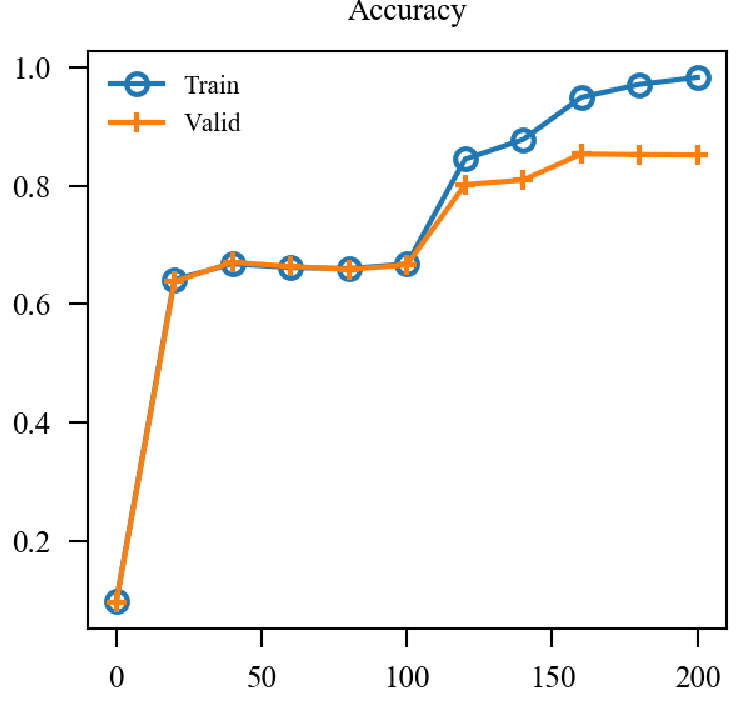
| TN |  |
 |
 |
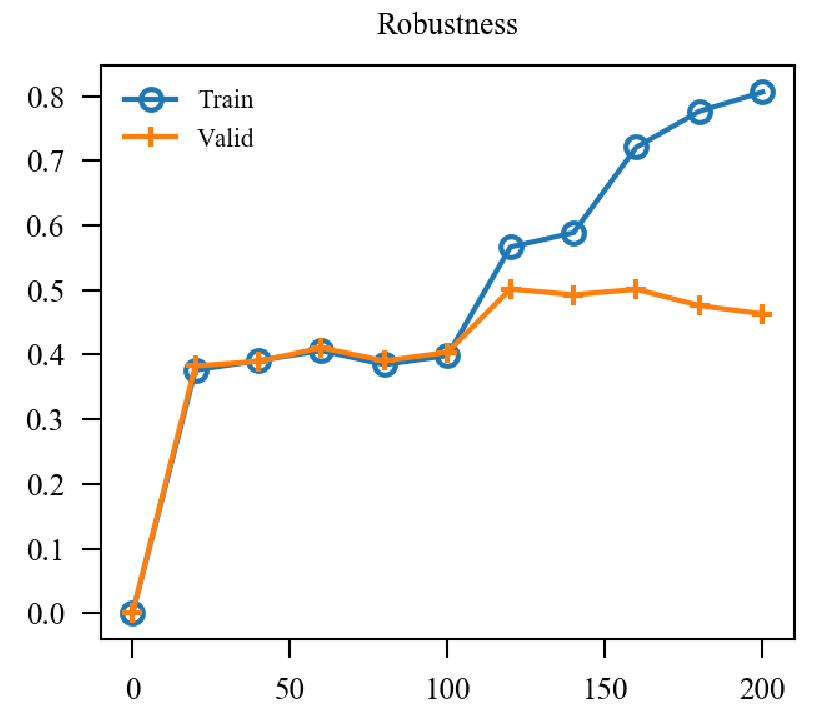用了两个BN后的确稳定下来了, 精度和鲁棒性的确和标准的AT一致了. 但是也仅仅是一致而已, 个人感觉noise太容易被分辨出来了, 或许增大攻击noise的epsilon会有改进, 后续再看.
