Categorical Reparameterization with Gumbel-Softmax
概
利用梯度反向传播训练网咯几乎是深度学习的不二法门, 但是这往往要求保证梯度的存在, 这在一定程度上限制了一些扩展. 比如在VAE中, 虽然当\(q_{\phi}(z|x)\)是一个正态分布的时候, 我们可以利用reparameterization来保证梯度存在, 即:
\[z = \mu + \sigma \cdot \epsilon, \quad \epsilon \sim \mathcal{N}(0, I).
\]
但是倘若中间变量是离散变量, 比如我们期望构建一个条件的VAE, 那么我们就没法用这种方式来解决了, 本文就提出了一个对离散分布的近似.
主要内容
Gumbel distribution
由gumbel distribution的性质可以知道, 从离散分布中采样\([\pi_1, \cdots, \pi_k]\)等价于
\[z = \mathrm{one\_hot}(\arg \max_i [g_i + \log \pi_i]), \quad g_i \mathop{\sim}\limits^{i.i.d.} \mathrm{Gumbel}(0, 1), i=1,2, \cdots, k.
\]
又\(\arg \max\) 可的一个连续逼近为softmax, 即
\[y_i = \frac{\exp((g_i + \log \pi_i) / \tau)}{\sum_{j=1}^k \exp((g_j + \log \pi_j) / \tau)}, i=1,2\cdots, k.
\]
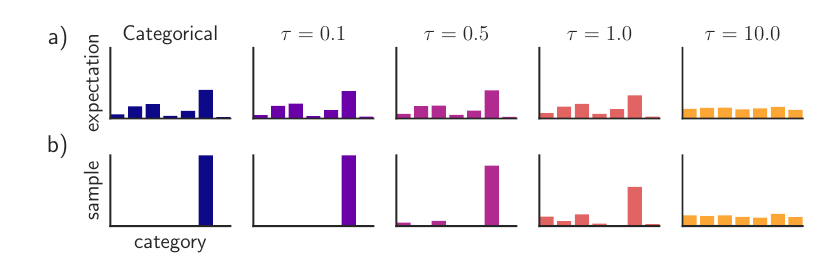
可以发现, 当\(\tau\)比较小的时候, Gumbel-Softmax分布的期望和离散分布的期望是一致的, 采样的情况也是相同的, 我们可以选择一个较小的\(\tau\)使得Gumbel-Softmax分布是离散分布的一个连续近似.
注: 作者偏爱先取一个较大的\(\tau\), 再退火至一个小的\(\tau=0.5\).
注: 作者在概率密度函数的推导过程中, 即公式(15)出有一个小错误, 应当是\(e^{-v}\)而非\(e^{x_k -v}\).
