EMA

目录

• 源
• 设置
• 结果

源

Exponential moving average (EMA) 是一个非常有用的trick, 起到加速训练的作用. 近来发现, 该技巧还可以用于提高网络鲁棒性(约1% ~ 2%). EMA的流程很简单, \(f(\cdot;\theta)\)是我们用于训练的网络, 则在每次迭代结束后进行:

\[\theta' = \alpha \cdot \theta' + (1 - \alpha) \cdot \theta, \]

其中\(\theta'\)是\(f'(\cdot; \theta')\)网络的参数, \(f', f\)的网络初始化是一致的, 另外\(f'\)的网络参数的更新仅仅通过上式.

一般情况下, 对抗训练用\(f(\cdot; \theta)\)来生成对抗样本, 即

\[x_{adv} := \arg \max_{\|x'-x\|\le \epsilon} \mathcal{L}(f(x'),y), \]

来获得, 而我想的能不能

\[x_{adv} := \arg \max_{\|x'-x\|\le \epsilon} \mathcal{L}(f'(x'),y). \]

背后的直觉是, \(f'\)相较于\(f\)更为平稳, 则由其产生的对抗样本的分布更加稳定, 则\(f\)拟合起来会不会更加容易?

我在一个8层的网络上进行测试, 结果不如人意:

设置

model	cifar
dataset	CIFAR-10
attack	PGD
epsilon	8/255
stepsize	2/255
steps	10
loss	cross entropy
optimizer	sgd
momentum	0.9
beta1	0.9
beta2	0.999
weight_decay	2e-4
leaning_rate	0.1
learning_policy	AT
epochs	200
batch_size	128
transform	default
seed	1
alpha	0.999

结果

	Accuracy	Robustness
EMA*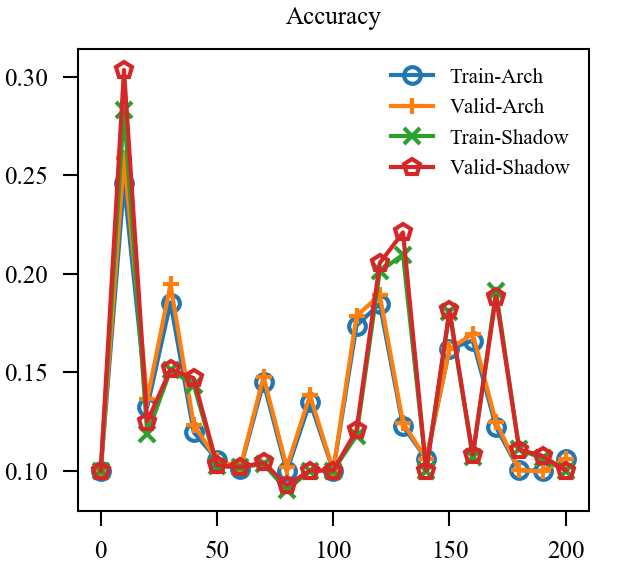
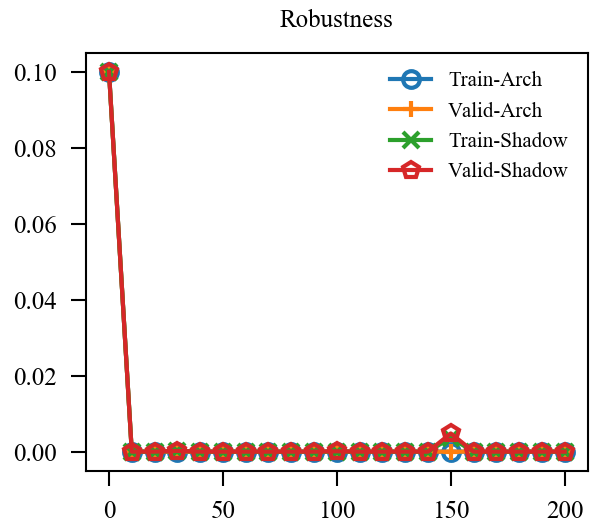EMA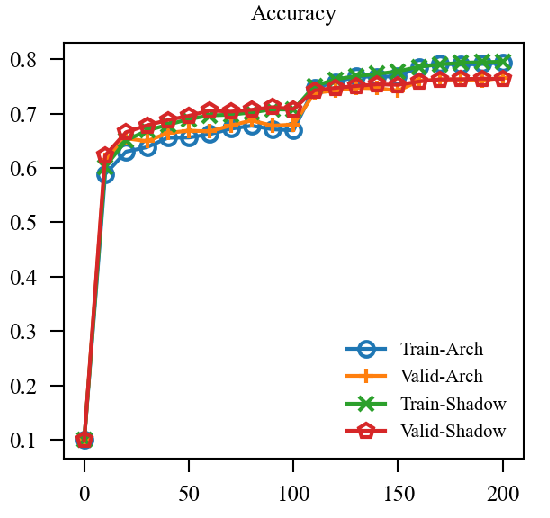
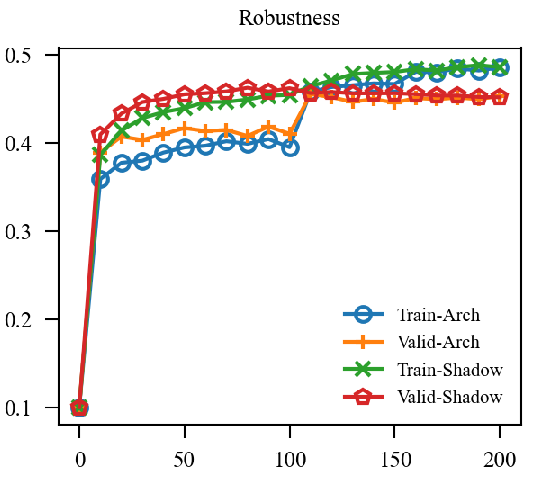EMA + GroupNorm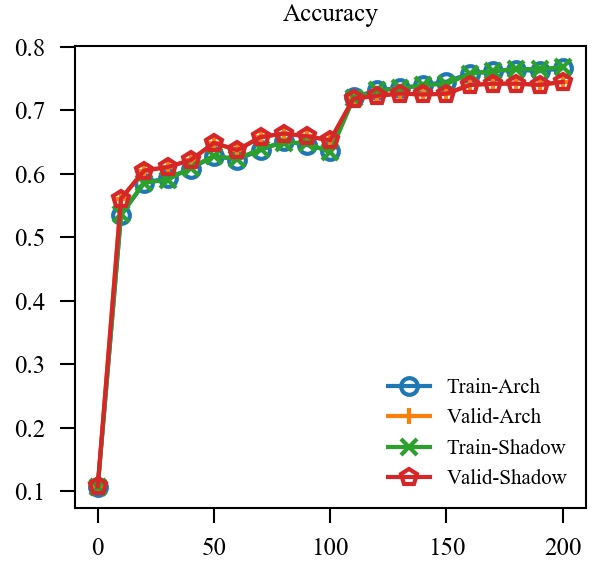

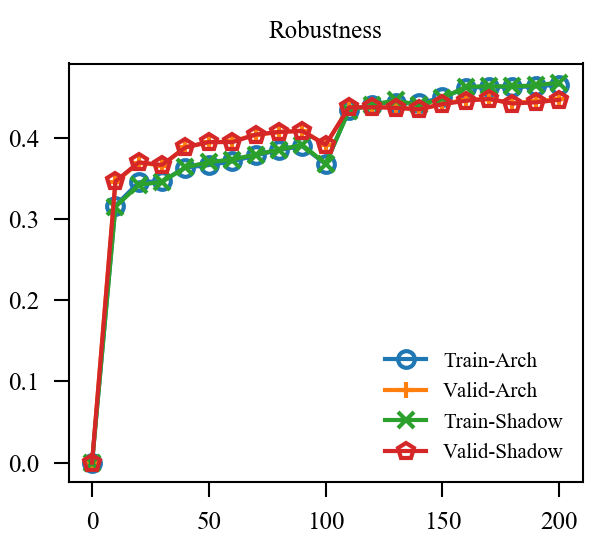上图中, EMA是原本的逻辑, 可见其的确能加速训练(Shadow表示\(f'\)), 虽然最后的结果是降了点, 这主要是参数没调好, 毕竟对抗训练很容易过拟合. 但是我们的直接却完全不起作用, 这让我非常困惑, 因为, 我料想的最差的结果, 也应当是鲁棒性不怎样, 不能精度和鲁棒性都很差, 因为虽然是通过\(f'\)生成的对抗样本, 这些对抗样本依旧是满足$|x_{adv} - x|_{\infty} \le 8 /255 $ 的，所以应该是没问题的.

于是我又尝试让\(\alpha\)由\(0\)慢慢增加到\(0.999\), 但是结果依然不容乐观. 我料想是batch normalization的问题, 于是换了group normlization:

虽然结果似乎表明我们的直觉完全是错误的, 但是还是体会到了 normalization 的重要性, BN很难应对不同分布.