Causal Intervention for Weakly-Supervised Semantic Segmentation

目录

• 概
• 主要内容
  • 普通的弱监督语义分割
  • 因果模型
  • 训练流程
• 代码

Zhang D., Zhang H., Tang J., Hua X. and Sun Q. Causal Intervention for Weakly-Supervised Semantic Segmentation. NIPS, 2020.

概

这篇文章从因果关系的角度剖析如何提升弱监督语义分割的方法.

主要内容

普通的弱监督语义分割

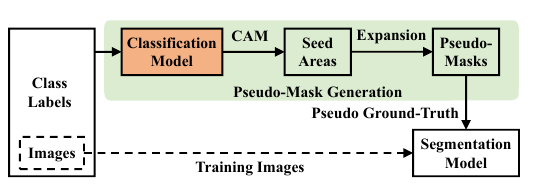
弱监督语义分割不似普通的语义分割一样依赖丰富的人工标注, 本文考虑的情况就是非常极限的, 仅知道每张图片的类别标签(可以是多标签, 比如: 人, 车, 表示一张图片里面有人有车).

一般的弱监督语义分割包含:

1. 训练一个分类模型(多标签);
2. 通过CAM确定大概的seed areas;
3. 将seed areas进行拓展得到pseudo-masks;
4. 训练一个分割模型(将pseudo-masks作为ground-truth);
5. 概分割模型作为最后的模型

但是显然的是, 仅仅凭借类别标签完成复杂的语义分割任务是相当困难的, 大概有如下:

1. 目标物体往往不是孤立的: 有可能数据集中每次出现马的时候都会有一个人, 则分类模型可能会将二者的特征混合用于分类, 那么最后的分割就很难明显的把二者的边界提取出来;
2. 背景信息并不完全: 背景往往含有一些别的未被标注的目标, 而这些目标和我们所关心的目标有可能是相互联系甚至是同时存在的, 比如: 地板和沙发, 这导致在提取沙发的时候往往把模板也一并提取出来了;
3. foreground, 前景的目标往往是共同变化的: 比如车和车窗, 车窗总是会反应周围的事物, 导致车窗这一属性不是用来提取车的好的特征, 分类模型很有可能会丢掉这一部分信息, 其导致的结果就是最后的分割的区域车窗少一块.

因果模型

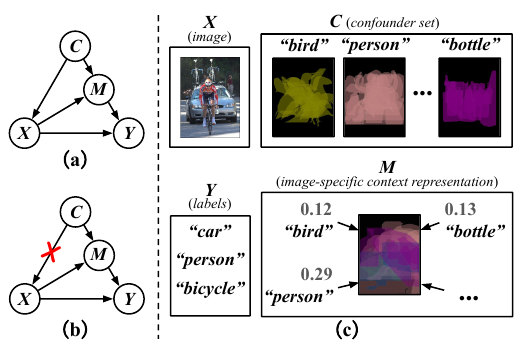
C: context prior;
X: pixel-level image;
M: image-specific representation using the textual templates from C;
Y: labels.

作者认为, 整个流程是这样的:

1. 确定先验背景信息$C$;
2. 通过先验背景信息$C$构建图片$X$;
3. 图片$X$和背景信息$C$共同确定了和背景有关的特征表示$M$;
4. $X$, $M$ 共同影响最后的类别标签$Y$.

我们一般的分类模型, 实际上是拟合条件分布

$$\mathrm{P}[Y|X],$$

显然这个条件分布与先验的背景信息有很大联系, 即图(a).
而我们实际上所关心的是

$$\mathrm{P}[Y|do(X)],$$

即建立目标的出现和场景没有关系的模型.
首先我们要做的就是将其转为一般的统计估计量:

$$\tag{1} \begin{array}{rl} \mathrm{{P}}[Y|do(X)] =& \sum_{c} \mathrm{P}[Y|do(X), c] \: \mathrm{P}[c|do(x)]\\ =& \sum_{c} \mathrm{P}[Y|do(X), c] \: \mathrm{P}[c]\\ =& \sum_{c} \mathrm{P}[Y|X, c, f(X;c)] \: \mathrm{P}[c]\\ =& \sum_{c} \mathrm{P}[Y|X, M=f(X;c)] \: \mathrm{P}[c].\\ \end{array}$$

显然, 这里有一个假设, 即知道了$X, C$之后, $M$也是确定的, 其通过$M=f(X;c)$来拟合.

训练流程

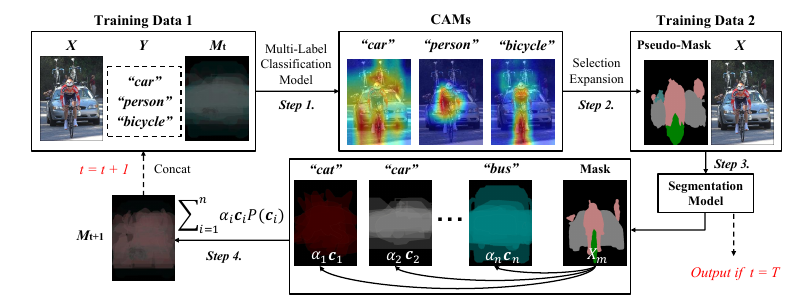
1. 训练以$X, M$为输入的多标签分类网络, 其通过

$$\mathrm{P}[Y|do(X);\Theta_t] = \prod_{i=1}^n [\mathbf{1}_{i \in Y}\frac{1}{1 + \exp(-s_i)} + \mathbf{1}_{i \not\in Y}\frac{1}{1 + \exp(s_i)} ],$$

其中$s_i=f(X, M_t;\theta_t^i)$, $n$是类别总数.
2. 利用CAM得到seed areas 并扩展为pseudo-mask;
3. 将上面的pseudo-mask作为ground-truth训练分割模型;
4. 计算

$$M_{t+1} = \sum_{i=1}^n \alpha_i c_i P(c_i), \quad \alpha_i = softmax(\frac{(W_1X_m)^T(W_2c_i)}{\sqrt{n}}).$$

注意到, 我们本应该最小化(1), 但是注意到, 此时对于每一个$c$, 我们都要循环一次, 这非常非常耗时, 所以作者是:

$$\sum_{c} \mathrm{P}[Y|do(X), M=f(X;c)] \mathrm{P}[c]\approx \mathrm{P}[Y|do(X), M=\sum_{c}f(X;c)\mathrm{P}(c) ].\\ $$

一直进行$T$步.

注:第1步中的$f(X, M_t;\theta_t^i)$并不一定要让$X, M_t$都在同一层输入, 实际上$M_t$是比较抽象的信息, 故作者实验发现在后几个block加入效果更好;

注: 先验背景信息$\{c_i\}$是pseudo-mask的平均;

注: $W_1, W_2$是可训练的参数.

代码

原文代码