Causal Inference

Hern $\'{a}$ n M. and Robins J. Causal Inference: What If.

Neal B. Introduction to Causal Inference.

这里对常用的causal effect的估计方法做一个总结, 需要注意的是, 在参数模型的情况下 $\theta L$ 表示 $\theta^TL$ 当二者为向量的时候.
为了方便, 我们常常使用 $\sum$ , 这并非要求该项必须是离散的, 除了 $A$ 大部分可以等价于 $\int$ .

默认情况下, (条件)可交换性(exchangeability), 一致性(consistency) 以及正性(positivity) 都是满足的, 特别的情况为注明.
其中, time-varying的条件可交换性定义为:

(Y^{g}, {\underline{L}}_{k + 1}^{g}) ⨿ A_{k} | {\bar{A}}_{k - 1} = g ({\bar{A}}_{k - 2}, {\bar{L}}_{k - 1}), {\bar{L}}_{k}, k = 0, \dots, K .

$(Y^g, \underline{L}_{k+1}^g) \amalg A_k | \bar{A}_{k-1} = g(\bar{A}_{k-2},\bar{L}_{k-1}), \bar{L}_{k}, \: k=0,\cdots, K.$

如果是静态的, $g$ 换成 $\bar{a}$ .

Censoring 是数据缺失的情况, 对其的处理可以理解为对多个treatments的情况的处理.

Standardization

非参数情况

E [Y^{a}] = E [Y^{a} | A = a] = E [Y | A = a] .

$\mathbb{E}[Y^a] = \mathbb{E}[Y^a|A=a]= \mathbb{E}[Y|A=a].$

\begin{matrix} (S) & E [Y^{a}] = E_{L} E_{Y^{a}} [Y^{a} | L] = E_{L} E_{Y} [Y | A = a, L] . \end{matrix}

$\tag{S} \mathbb{E}[Y^a] = \mathbb{E}_{L} \mathbb{E}_{Y^a}[Y^a|L] =\mathbb{E}_{L} \mathbb{E}_{Y}[Y|A=a, L].$

具体地, 为

\begin{matrix} (S+) & \sum_{l} E [Y | A = a, L = l] P r [L = l], \end{matrix}

$\tag{S+} \sum_l \mathbb{E}[Y|A=a, L=l] \mathrm{Pr}[L=l],$

所以该式必须满足正性, 即

P r [A = a | L = l] > 0, i f P r [L = l] > 0,

$\mathrm{Pr}[A=a|L=l] > 0, \quad \mathrm{if}\: \mathrm{Pr}[L=l] > 0,$

否则 $\mathbb{E}[Y|A=a, L=l]$ 无定义.

Censoring

E [Y^{a, c = 0}] = E_{L} E [Y | A = a, C = 0, L] .

$\mathbb{E}[Y^{a, c=0}] = \mathbb{E}_{L} \mathbb{E}[Y|A=a, C=0, L].$

参数模型

标准化处理的参数模型, 就是估计

\hat{E} [Y | A = a, L = l],

$\hat{\mathbb{E}} [Y|A=a, L=l],$

比如:

\hat{E} [Y | A, L] = θ_{0} + θ_{1} A + θ_{2} L + θ_{3} A L .

$\hat{\mathbb{E}} [Y|A, L] = \theta_0 + \theta_1A + \theta_2L + \theta_3 AL.$

接下来用(S, S+)的公式就可以了(一般是直接用S, 根据大数定律弄的).

Time-varying

静态

\begin{aligned} \sum_{{\bar{l}}_{K}} E [Y | {\bar{A}}_{K} = {\bar{a}}_{K}, {\bar{L}}_{K} = {\bar{l}}_{K}] \prod_{k = 0}^{K} f (l_{k} | {\bar{a}}_{k - 1}, {\bar{l}}_{k - 1}) \\ = & \sum_{{\bar{l}}_{K}} E [Y | {\bar{A}}_{K - 1} = {\bar{a}}_{K - 1}, {\bar{L}}_{K} = {\bar{l}}_{K}] \prod_{k = 0}^{K} f (l_{k} | {\bar{a}}_{k - 1}, {\bar{l}}_{k - 1}) \\ = & \sum_{{\bar{l}}_{K}} E [Y, {\bar{A}}_{K - 1} = {\bar{a}}_{K - 1}, {\bar{L}}_{K} = {\bar{l}}_{K}] \prod_{k = 0}^{K - 1} f (l_{k} | {\bar{a}}_{k - 1}, {\bar{l}}_{k - 1}) \cdot f ({\bar{a}}_{k - 1}, {\bar{l}}_{k - 1}) \\ = & \sum_{{\bar{l}}_{K}} E [Y | {\bar{A}}_{K - 1} = {\bar{a}}_{K - 1}, {\bar{L}}_{K} = {\bar{l}}_{K - 1}] \prod_{k = 0}^{K - 1} f (l_{k} | {\bar{a}}_{k - 1}, {\bar{l}}_{k - 1}) \\ = & \dots \\ = & E [Y^{\bar{a}}] . \end{aligned}

$\begin{array}{rl} {}& \sum_{\bar{l}_K} \mathbb{E}[Y|\bar{A}_K=\bar{a}_K, \bar{L}_K=\bar{l}_K] \prod_{k=0}^K f(l_k|\bar{a}_{k-1}, \bar{l}_{k-1}) \\ =& \sum_{\bar{l}_K} \mathbb{E}[Y|\bar{A}_{K-1}=\bar{a}_{K-1}, \bar{L}_K=\bar{l}_K] \prod_{k=0}^K f(l_k|\bar{a}_{k-1}, \bar{l}_{k-1}) \\ =& \sum_{\bar{l}_K} \mathbb{E}[Y,\bar{A}_{K-1}=\bar{a}_{K-1}, \bar{L}_K=\bar{l}_K] \prod_{k=0}^{K-1} f(l_k|\bar{a}_{k-1}, \bar{l}_{k-1}) \cdot f(\bar{a}_{k-1}, \bar{l}_{k-1}) \\ =& \sum_{\bar{l}_K} \mathbb{E}[Y|\bar{A}_{K-1}=\bar{a}_{K-1}, \bar{L}_K=\bar{l}_{K-1}] \prod_{k=0}^{K-1} f(l_k|\bar{a}_{k-1}, \bar{l}_{k-1})\\ =& \cdots \\ =& \mathbb{E}[Y^{\bar{a}}]. \end{array}$

至于动态的, 书上给出了一个公式, 但是我感觉不是很对, 这里推导一下试试:

\begin{aligned} E [Y^{g}] \\ = & E_{\bar{a} \sim g} E_{Y} [Y^{\bar{a}}] \\ = & \sum_{\bar{a} \sim g} \sum_{\bar{l}} E [Y^{\bar{a}} | \bar{A} = \bar{a}, L = \bar{l}] \cdot f (\bar{A}, \bar{L}), \end{aligned}

$\begin{array}{rl} {}& \mathbb{E}[Y^g] \\ =& \mathbb{E}_{\bar{a}\sim g} \mathbb{E}_Y [Y^{\bar{a}}] \\ =&\sum_{\bar{a}\sim g} \sum_{\bar{l}} \mathbb{E}[Y^{\bar{a}}|\bar{A}=\bar{a}, L=\bar{l}] \cdot f(\bar{A}, \bar{L}), \\ \end{array}$

其中

P r (\bar{A}, \bar{L}) = \prod_{k = 0}^{K} f (L_{k} | {\bar{A}}_{k - 1}, {\bar{L}}_{k - 1}) \cdot \prod_{k = 0}^{K} f^{i n t} (A_{k} | {\bar{A}}_{k - 1}, {\bar{L}}_{k}) .

$\mathrm{Pr}(\bar{A}, \bar{L}) = \prod_{k=0}^K f(L_k|\bar{A}_{k-1}, \bar{L}_{k-1}) \cdot \prod_{k=0}^K f^{int}(A_k|\bar{A}_{k-1}, \bar{L}_{k}).$

这里, $f^{int}$ 表示每一步 $g$ 的根据前面历史选择 $A_k$ 的概率.

IP weighting

无参数

E [\frac{I (A = a) Y}{f (A | L)}] = E_{L} {E_{Y} [Y^{a} | L] \cdot \underset{= 1}{\underset{⏟}{E_{A} [\frac{I (A = a)}{f (A | L)} | L]}}} = E [Y^{a}] .

$\mathbb{E}[\frac{I(A=a)Y}{f(A|L)}] = \mathbb{E}_L \{\mathbb{E}_Y [Y^a|L] \cdot \underbrace{\mathbb{E}_{A}[\frac{I(A=a)}{f(A|L)}|L]}_{=1}\} = \mathbb{E}[Y^a].$

倘若 $A$ 为连续变量, $f$ 为对应的条件密度函数, 则(非零的部分是零测集)

E [\frac{I (A = a) Y}{f (A | L)}] \equiv 0.

$\mathbb{E}[\frac{I(A=a)Y}{f(A|L)}] \equiv 0.$

当正性不成立的时候, 即存在 $l$ , $\mathrm{Pr}[L=l] > 0$ , 但是 $f(A=0|L=l) = 0$ , 此时

\begin{aligned} E [\frac{I (A = a) Y}{f (A | L)}] & = E_{L \in Q (a)} {E [Y^{a} | L = l] \cdot E_{A} [\frac{I (A = a)}{f (A | L)} | L]} \\ = E_{L \in Q (a)} {E [Y^{a} | L = l]} \\ = E [Y^{a} | L \in Q (a)] P r [L \in Q (a)] . \end{aligned}

$\begin{array}{rl} \mathbb{E}[\frac{I(A=a)Y}{f(A|L)}] &= \mathbb{E}_{L \in Q(a)} \{\mathbb{E}[Y^a|L=l]\cdot \mathbb{E}_{A}[\frac{I(A=a)}{f(A|L)}|L]\} \\ &= \mathbb{E}_{L \in Q(a)} \{\mathbb{E}[Y^a|L=l]\} \\ &= \mathbb{E}[Y^a|L\in Q(a)]\mathrm{Pr}[L\in Q(a)]. \\ \end{array}$

Censoring

E [Y^{a, c = 0}] = E [\frac{I (A = a, C = 0) Y^{a}}{f (A | L) f (C | A, L)}] .

$\mathbb{E}[Y^{a, c=0}] = \mathbb{E}[\frac{I(A=a, C=0)Y^a}{f(A|L)f(C|A,L)}].$

参数模型

定义

W^{A} = f (A | L),

$W^A = f(A|L),$

需要说明的是

\begin{matrix} (IP) & E [Y^{a}] = \frac{E [I (A = a) W^{A} Y]}{E [I (A = a) W^{A}]} . \end{matrix}

$\tag{IP} \mathbb{E}[Y^a] = \frac{\mathbb{E}[I(A=a)W^AY]}{\mathbb{E}[I(A=a)W^A]}.$

注: 实际上分母为1.

特别的, 可以定义

S W^{A} = f (A) / f (A | L),

$SW^A = f(A) / f(A|L),$

\begin{matrix} (IP+) & E [Y^{a}] = \frac{E [I (A = a) S W^{A} Y]}{E [I (A = a) S W^{A}]} . \end{matrix}

$\tag{IP+} \mathbb{E}[Y^a] = \frac{\mathbb{E}[I(A=a)SW^AY]}{\mathbb{E}[I(A=a)SW^A]}.$

注: 此时分母为 $f(A)$ . 在估计中, (IP+)更为稳定.

显然, 在参数模型中, 我们常常需要建模:

\hat{f} (A | L),

$\hat{f}(A|L),$

并得到

{\hat{W}}^{A} o r {\hat{S W}}^{A} .

$\widehat{W}^A \quad \mathrm{or} \quad \widehat{SW}^A.$

此时再进一步假设

\hat{E} [Y^{a}],

$\hat{\mathbb{E}} [Y^a],$

比如

\hat{E} [Y^{a}] := θ_{0} + θ_{1} a .

$\hat{\mathbb{E}} [Y^a] := \theta_0 + \theta_1 a.$

通过 $\widehat{W}$ 或者 $\widehat{SW}$ 得到 $\mathbb{E}[Y^a]$ 的近似值:

\frac{\sum_{i} I (A = a) W_{i} Y_{i}}{\sum_{i} I (A = a) W_{i}}, o r \frac{\sum_{i} I (A = a) S W_{i} Y_{i}}{\sum_{i} I (A = a) S W_{i}} .

$\frac{\sum_i I(A=a)W_iY_i}{\sum_i I(A=a)W_i}, \quad \mathrm{or} \quad \frac{\sum_i I(A=a)SW_iY_i}{\sum_i I(A=a)SW_i}.$

通过最小二乘法来估计参数 $\theta_0, \theta_1$ .

注: 一般情况下( $A$ 低维的情况), $f(A)$ 可以通过无参数估计估计, 否则也需要建模估计.

IP weighting 有一种特别好的思路, 主要到, 经过weighting之后, 相当于我们重新选择了 $A$ , 此时 $A$ 和 $L$ 无关, 在这个伪造的人群中, 我们有

E_{p s} [Y | A = a] = E [Y^{a}] .

$\mathbb{E}_{ps}[Y|A=a] = \mathbb{E}[Y^a].$

注: 证明只需要用到 $A \amalg L$ .

注: 在这种可建模的情况下, 正性并不重要, 而且似乎即使 $A$ 是连续变量, 上述的估计方式也是奏效的, 但是说实话我无法理解.

censoring

如果由censoring的情况出现, 只需要考虑

W^{A C} = W^{A} \cdot W^{C}, S W^{A C} = S W^{A} \cdot S W^{C},

$W^{AC} = W^A \cdot W^C, \\ SW^{AC} = SW^A \cdot SW^C, \\$

其中

W^{C} = 1 / f (C | A, L), S W^{C} = f (C | A) / f (C | A, L) .

$W^C = 1 / f(C|A, L), \\ SW^C = f(C|A) / f(C|A, L).$

条件下 V

如何用IP weighting 估计

E [Y^{a} | V], V \subset L .

$\mathbb{E}[Y^a|V], V \subset L.$

只需考虑

W^{A} = 1 / f (A | V, L ∖ V), S W^{A} = f (A | V) / f (A, V, L ∖ V) .

$W^A = 1 / f(A| V, L\setminus V), \\ SW^A = f(A|V) / f(A, V, L\setminus V).$

分别利用(IP, IP+)即可.

注: 此时二者分母均不为1, 故不可用最普通的IP weighting的公式.

Time-varying

此时

W^{\bar{A}} = \prod_{k = 0}^{K} \frac{1}{f (A_{k} | {\bar{A}}_{k - 1}, {\bar{L}}_{k})}, S W^{\bar{A}} = \prod_{k = 0}^{K} \frac{f (A_{k} | {\bar{A}}_{k - 1})}{f (A_{k} | {\bar{A}}_{k - 1}, {\bar{L}}_{k})} .

$W^{\bar{A}} = \prod_{k=0}^K \frac{1}{f(A_k|\bar{A}_{k-1}, \bar{L}_k)}, \\ SW^{\bar{A}} = \prod_{k=0}^K \frac{f(A_k|\bar{A}_{k-1})}{f(A_k|\bar{A}_{k-1}, \bar{L}_k)}. \\$

剩下的就是利用类似(IP, IP+)的公式计算.

在这种情况下, 同样有条件下V, 但是, 特别的是, $V$ 必须是baseline variables, 即

V \subset L_{0} .

$V \subset L_0.$

注: 没看到其用于动态策略的是说明.

G-estimation

非参数模型

非参数模型可以看成是参数模型的一种特例.

参数模型

这个方法主要是用于估计

E [Y^{a} | L] - E [Y^{a^{'}} | L] .

$\mathbb{E}[Y^a|L] -\mathbb{E}[Y^{a'}|L].$

假设

\hat{E} [Y^{a} | L] = β_{0} + β_{1} a + β_{2} L + θ_{3} a L,

$\hat{\mathbb{E}} [Y^a|L] = \beta_0 + \beta_1 a + \beta_2 L + \theta_3 aL,$

则

E [Y^{a} | L] - E [Y^{a = 0} | L] = β_{1} a + β_{3} a V .

$\mathbb{E}[Y^a|L] -\mathbb{E}[Y^{a=0}|L] = \beta_1 a + \beta_3 aV.$

假设 rank preserving 成立, 则有

Y^{a} = Y^{a = 0} + ψ_{0} a + ψ_{1} a V, \Rightarrow Y^{a = 0} = Y - ψ_{0} a - ψ_{1} a V,

$Y^a = Y^{a=0} + \psi_0 a + \psi_1 aV, \\ \Rightarrow Y^{a=0} = Y - \psi_0 a - \psi_1 a V,$

并定义 $H(\psi^{\dagger}):= Y^{a=0}$ .

注意到, 条件可交换性

Y^{a} ⨿ A | L

$Y^a \amalg A |L$

意味着

P r [A = 1 | Y^{a = 0}, L] = P r [A = 1 | L] .

$\mathrm{Pr}[A=1|Y^{a=0}, L] = \mathrm{Pr}[A=1|L].$

假设我们用一个逻辑斯蒂回归对其进行建模:

l o g i t P r [A = 1 | Y^{a = 0}, L] = θ_{0} + θ_{1} Y^{a = 0} + θ_{2} Y^{a = 0} V + θ_{3} L .

$\mathrm{logit}\: \mathrm{Pr}[A=1|Y^{a=0}, L] = \theta_0 + \theta_1 Y^{a=0} + \theta_2 Y^{a=0}V + \theta_3 L.$

则根据条件可交换性的性质, $\theta_1, \theta_2$ 都应该是0, 现在 $H(\psi^{\dagger})=Y^{a=0}$ , 则

l o g i t P r [A = 1 | H (ψ^{†}), L] = θ_{0} + θ_{1} H (ψ^{†}) + θ_{2} H (ψ^{†}) V + θ_{3} L .

$\mathrm{logit}\: \mathrm{Pr}[A=1|H(\psi^{\dagger}), L] = \theta_0 + \theta_1 H(\psi^{\dagger})+ \theta_2 H(\psi^{\dagger})V + \theta_3 L.$

给定 $\psi_0, \psi_1$ , 我们可以估计出一组 $\theta_0, \cdots, \theta_3$ , 什么样的 $\psi_0, \psi_1$ 是好的, 就是让估计的参数 $\theta_1, \theta_2$ 接近0.
所以 G-estimation 常用网格法来估计.
不过应对高维问题的时候就比较捉襟见肘了.
在特殊的情况下, 我们可以有显示的表达式.

Time-varying

类似.

\hat{E} [Y^{{\bar{a}}_{k - 1}, a_{k}, {\underline{0}}_{k + 1}} - Y^{{\bar{a}}_{k + 1}, {\underline{0}}_{k}} | {\bar{A}}_{k - 1} = {\bar{a}}_{k - 1}, {\bar{L}}_{k} = {\bar{l}}_{k}] = a_{k} γ_{k} ({\bar{a}}_{k - 1} {\bar{l}}_{k}; β) .

$\hat{\mathbb{E}}[Y^{\bar{a}_{k-1}, a_k, \underline{0}_{k+1}} - Y^{\bar{a}_{k+1}, \underline{0}_{k}}|\bar{A}_{k-1}=\bar{a}_{k-1}, \bar{L}_k = \bar{l}_k] = a_k \gamma_k (\bar{a}_{k-1}\bar{l}_k; \beta).$

Y^{{\bar{A}}_{k - 1}, A_{k}, {\underline{0}}_{k + 1}} = Y^{{\bar{A}}_{k + 1}, {\underline{0}}_{k}} + A_{k} γ_{k} ({\bar{A}}_{k - 1}, {\bar{l}}_{k}; β) .

$Y^{\bar{A}_{k-1}, A_k, \underline{0}_{k+1}} =Y^{\bar{A}_{k+1}, \underline{0}_{k}} + A_k \gamma_k (\bar{A}_{k-1}, \bar{l}_k ;\beta).$

H_{k} (ψ^{†}) = Y - \sum_{j = k}^{K} A_{j} γ_{j} ({\bar{A}}_{j - 1}, {\bar{L}}_{j}, ψ^{†}) .

$H_k(\psi^{\dagger}) = Y - \sum_{j=k}^K A_j \gamma_j(\bar{A}_{j-1}, \bar{L}_{j}, \psi^{\dagger}).$

通过下式来估计:

l o g i t P r [A_{k} = 1 | H_{k} (ψ^{†}), {\bar{L}}_{k}, {\bar{A}}_{k - 1}] = α_{0} + α_{1} H_{k} (ψ^{†}) + α_{2} W_{k} .

$\mathrm{logit}\:\mathrm{Pr} [A_k=1|H_k(\psi^{\dagger}), \bar{L}_k, \bar{A}_{k-1}] = \alpha_0 + \alpha_1 H_k(\psi^{\dagger}) + \alpha_2 W_k.$

Propensity Scores

该方法仅能应用于二元情形, 即 $A \in \{0, 1\}$ .
当 $L$ 是一个高维向量的时候, 一般的无参数模型就派不上用场了, 尽管我们可以通过参数模型来建模, 但是带来的结果是估计结果的方差会比较大.

我们记 $\pi(L) = \mathrm{Pr}[A|L]$ , 并证明:

Y^{a} ⨿ A | L \Rightarrow Y^{a} ⨿ A | π (L) .

$Y^a \amalg A | L \Rightarrow Y^a \amalg A | \pi(L).$

不妨假设 $\pi(L) =s \Leftrightarrow L \in \{l_i\}$ , 则

\begin{array}{ll} P r [Y^{a} | π (L) = s] & = P r [Y^{a} | L \in {l_{i}}] \\ = \frac{\sum_{i} P r [Y^{a}, L = l_{i}]}{\sum_{i} P r [L = l_{i}]} \\ = \frac{\sum_{i} P r [Y | A = a, L = l_{i}] P r [L = l_{i}]}{\sum_{i} P r [L = l_{i}]} \\ = \frac{P r [A = a | L = l] \cdot \sum_{i} P r [Y | A = a, L = l_{i}] P r [L = l_{i}]}{P r [A = a | L = l] \sum_{i} P r [L = l_{i}]} \\ = \frac{\sum_{i} P r [Y | A = a, L = l_{i}] P r [A = a, L = l_{i}]}{\sum_{i} P r [A = a, L = l_{i}]} \\ = \frac{\sum_{i} P r [Y, A = a, L = l_{i}]}{\sum_{i} P r [A = a, L = l_{i}]} \\ = \frac{P r [Y, A = a, π (L) = s]}{P r [A = a, π (L)]} \\ = P r [Y | A = a, π (L) = s] . \end{array}

$\begin{array}{ll} \mathrm{Pr}[Y^a|\pi(L)=s] &= \mathrm{Pr} [Y^a|L \in \{l_i\}] \\ &= \frac{\sum_i\mathrm{Pr}[Y^a,L=l_i]}{\sum_i \mathrm{Pr} [L=l_i]}\\ &= \frac{\sum_i\mathrm{Pr}[Y|A=a, L=l_i]\mathrm{Pr}[L=l_i]}{\sum_i \mathrm{Pr} [L=l_i]}\\ &= \frac{\mathrm{Pr}[A=a|L=l] \cdot \sum_i\mathrm{Pr}[Y|A=a, L=l_i]\mathrm{Pr}[L=l_i]}{\mathrm{Pr}[A=a|L=l]\sum_i \mathrm{Pr} [L=l_i]}\\ &= \frac{\sum_i\mathrm{Pr}[Y|A=a, L=l_i]\mathrm{Pr}[A=a, L=l_i]}{\sum_i \mathrm{Pr} [A=a, L=l_i]}\\ &= \frac{\sum_i\mathrm{Pr}[Y, A=a, L=l_i]}{\sum_i \mathrm{Pr} [A=a, L=l_i]}\\ &= \frac{\mathrm{Pr}[Y, A=a, \pi(L)=s]}{\mathrm{Pr} [A=a, \pi(L)]}\\ &= \mathrm{Pr} [Y|A=a, \pi(L)=s]. \end{array}$

注意: $\pi(l_i) = \pi(l_j) = \pi(l) = s$ .

可见, 上述推导仅在 $A$ 为二元变量是成立, 否则

P r [A = 1 | l] = P r [A = 1 | l^{'}] ⇏ P r [A = a^{'} | l] = P r [A = a^{'} | l^{'}] .

$\mathrm{Pr}[A=1|l] = \mathrm{Pr}[A=1|l'] \not \Rightarrow \mathrm{Pr}[A=a'|l] = \mathrm{Pr}[A=a'|l'].$

也就无法保证上面的推导证明对于所有的 $A=a$ 成立.

此时, 我们可以扩展causal graph为:

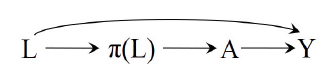
故, 我们可以通过 $\pi(L)$ 来block以保证条件可交换性.
剩下的工作就是利用前面的方法了.

Instrumental Variables

instrumental variables 满足:

Z 对 T 有 causal effect;
Z 到 Y 的 causal effect 均通过 T, 即 T 是 Z 到 Y 所有 direct path 上的mediator;
Z 和 Y 之间不存在backdoor path.

Binary Linear Setting

CAG图如上图所示.

Y := δ T + α U .

$Y := \delta T + \alpha U.$

\begin{aligned} E [Y | Z = 1] - E [Y | Z = 0] = & E [δ T + α U | Z = 1] - E [δ T + α U | Z = 0] \\ = & δ E [[T | Z = 1] - [T | Z = 0]] + α E [[U | Z = 1] - [U | Z = 0]] \\ = & δ E [[T | Z = 1] - [T | Z = 0]] \end{aligned}

$\begin{array}{rl} \mathbb{E}[Y|Z=1] - \mathbb{E}[Y|Z=0] =&\mathbb{E}[\delta T + \alpha U|Z=1] - \mathbb{E}[\delta T +\alpha U|Z=0] \\ =&\delta \mathbb{E}[[T|Z=1]-[T|Z=0]] + \alpha \mathbb{E}[[U|Z=1]-[ U|Z=0]] \\ =&\delta \mathbb{E}[[T|Z=1]-[T|Z=0]] \end{array}$

故

δ = \frac{E [Y | Z = 1] - E [Y | Z = 0]}{E [T | Z = 1] - E [T | Z = 0]} .

$\delta = \frac{\mathbb{E}[Y|Z=1] - \mathbb{E}[Y|Z=0]}{\mathbb{E}[T|Z=1] - \mathbb{E}[T|Z=0]}.$

注: 在此CAG图中, $U \amalg Z$ .

Continuous Linear Setting

依旧是如上的CAG图.

\begin{aligned} C o v (Y, Z) = & E [Y Z] - E [Y] E [Z] \\ = & δ (E [T Z] - E [T] E [Z]) + α (E [U Z] - E [U] E [Z]) \\ = & δ C o v (T, Z) + α C o v (U, Z) \\ = & δ C o v (T, Z) \end{aligned}

$\begin{array}{rl} \mathrm{Cov}(Y, Z) = & \mathbb{E}[YZ] - \mathbb{E}[Y]\mathbb{E}[Z] \\ =& \delta (\mathbb{E}[TZ] - \mathbb{E}[T]\mathbb{E}[Z]) + \alpha (\mathbb{E}[UZ] - \mathbb{E}[U]\mathbb{E}[Z]) \\ =& \delta \mathrm{Cov}(T, Z) + \alpha \mathrm{Cov}(U,Z)\\ =& \delta \mathrm{Cov}(T, Z) \end{array}$

故

δ = \frac{C o v (Y, Z)}{C o v (T, Z)} .

$\delta = \frac{\mathrm{Cov}(Y, Z)}{\mathrm{Cov}(T, Z)}.$

注: 依然用到了 $U \amalg Z$ .

Nonparametric Identification

仅考虑单个的二元变量 $T \in \{0, 1\}$ , 有如下几种情况:

Compliers: $T^{z=1}=1, T^{z=0}=0$ .
Always-takers: $T^{z=1}=1, T^{z=0}=1$ .
Never-takers: $T^{z=1}=0, T^{z=0}=0$ .
Defiers: $T^{z=1}=0, T^{z=0}=1$ .

当我们所考虑的群体中仅包括前三种类型的时候, 显然有:

T_{i}^{z = 1} \geq T_{i}^{z = 0} .

$T_i^{z=1} \ge T_i^{z=0}.$

这是我们需要的单调性假设.
此时:

E [Y^{t = 1} - Y^{t = 0} | T^{z = 1} = 1, T^{z = 0} = 0] = \frac{E [Y | Z = 1] - E [Y | Z = 0]}{E [T | Z = 1] - E [T | Z = 0]} .

$\mathbb{E}[Y^{t=1} - Y^{t=0}|T^{z=1}=1, T^{z=0}=0] = \frac{\mathbb{E}[Y|Z=1]-\mathbb{E}[Y|Z=0]}{\mathbb{E}[T|Z=1]-\mathbb{E}[T|Z=0]}.$

即, 在compliers (遵照医嘱的) 的人群中, 可以计算出其causal effect.
证明在[2]的p93.

Difference in Difference

difference in difference 同样是处理存在unobservable变量时的一种有效的处理方法.
我们可以把 $Y^a$ 拆成俩个阶段:

$t=0$ , 此时决定 $A$ , 但是并没有落实 $A$ ;
$t=1$ , 实行 $A$ .

凭借下面的假设:
1.

\forall t, A = a \Rightarrow Y_{t} = Y_{t}^{a} .

$\forall t, \quad A=a \Rightarrow Y_t = Y_t^a.$

$A=1$ , $A=0$ 两个群体若都不施加治疗, 则结果一致:

E [Y_{1}^{0} - Y_{0}^{0} | A = 1] = E [Y_{1}^{0} - Y_{0}^{0} | A = 0],

$\mathbb{E}[Y_1^0 - Y_0^0|A=1] =\mathbb{E}[Y_1^0 - Y_0^0|A=0],$

治疗前的状态一致:

E [Y_{0}^{1} - Y_{0}^{0} | A = 1] = 0.

$\mathbb{E}[Y_0^1 - Y_0^0|A=1]=0.$

注: 上面的第二条假设可能不容易满足.

则:

E [Y_{1}^{1} - Y_{1}^{0} | A = 1] = (E [Y_{1} | A = 1] - E [Y_{0} | A = 1]) - (E [Y_{1} | A = 0] - E [Y_{0} | A = 0]) .

$\mathbb{E}[Y_1^1-Y_1^0|A=1] =(\mathbb{E}[Y_1|A=1]-\mathbb{E}[Y_0|A=1]) -(\mathbb{E}[Y_1|A=0]-\mathbb{E}[Y_0|A=0]).$

Doubly Robust Estimator

未完待续

Instrumental variable estimation

未完待续

Stratification

未完待续

Matching

未完待续

posted @ 2021-03-31 20:04 馒头and花卷阅读(252) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

馒头and花卷

Causal Inference

Standardization

非参数情况

Censoring

参数模型

Time-varying

静态

IP weighting

无参数

Censoring

参数模型

censoring

条件下 V

Time-varying

G-estimation

非参数模型

参数模型

Time-varying

Propensity Scores

Instrumental Variables

Binary Linear Setting

Continuous Linear Setting

Nonparametric Identification

Difference in Difference

Doubly Robust Estimator

Instrumental variable estimation

Stratification

Matching

公告

搜索

随笔分类

Python相关

概率论-论文

收藏

优化问题-论文