Chapter 20 Treatment-Confounder Feedback
目录
在介绍如何估计causal effect之前, 需要介绍一个treatment-confounder feedback 的概念,
由于这种情况的存在, 导致原先的一些估计方法失效.
20.1 The elements of treatment-confounder feedback
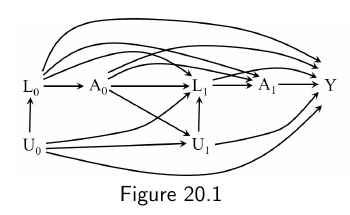
如图所示, \(L_1\)既受到treatment\(A_0\)的影响, 又会去影响下一个treatment\(A_1\), 这种情况就是 treatment-confounder feedback.

为了探究 treatment-confounder feedback 对causal effect估计的影响, 我们考虑一种简化的情况(如上图所示):
显然这种情况下, 是严格的sharp null hypothesis (因为没有由\(A_0, A_1\)指向\(Y\)的前向路径.)
20.2 The bias of traditional methods
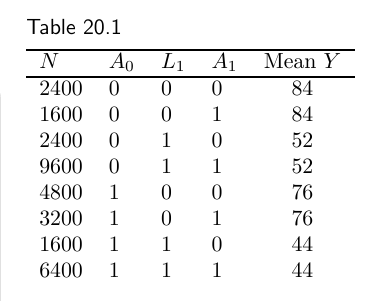
作者给出了一个具体的数据, 如上表所示.
用上表的数据计算, 可以很容易得出\(\mathbb{E}[Y^{a_0=1} -Y^{a_0=0}] = 0\), 关于\(a_1\)类同.
但是当我们关注\(\mathbb{E} [Y^{a_0=1, a_1=1} - Y^{a_0=0, a_1=0}]\)的时候就会出现问题, 首先要明确该式的值应当为0.
通过stratification 可以计算得到:
\[\mathbb{E}[Y|A_0=1, L_1=0, A_1=1] - \mathbb{E}[Y|A_0=0, L_1=0, A_1=0] = -8,
\mathbb{E}[Y|A_0=1, L_1=1, A_1=1] - \mathbb{E}[Y|A_0=0, L_1=1, A_1=0] = -8.
\]
所以根据stratification, 最后的causal effect 肯定是负的.
该方法失效了.
20.3 Why traditional methods fail
实际上, 原因自然就是
\[\mathbb{E}[Y|A_0=a_0, L_1=0, A_1=a_1] \not= \mathbb{E}[Y^{a_0,a_1}|L_1=0],
\]
特别地,
\[Y^{a_0, a_1} \not \amalg A_0 | L_1.
\]
注: 在这种情况下,
\[Y^{a_0, a_1} \amalg A_0 | L_1^{a_0}.
\]

