VAE with a VampPrior
概
这篇文章提出了一种新的"多模态"的先验.
主要内容
首先根据这里的推导可知,
\[\begin{array}{ll}
\mathcal{L}(\phi, \theta, \lambda)
=& \mathbb{E}_{q(x)} [\mathbb{E}_{q_{\phi}(z|x)}\log p_{\theta}(x|z)] \\
&+ \mathbb{E}_{x \sim q(x)}[\mathbb{H}[q_{\phi}(z|x)]] \\
&- \mathbb{E}_{z \sim q(z)}[-\log p_{\lambda}(z)].
\end{array}
\]
其中, \(q(z) = \frac{1}{N} \sum_{n=1}^{N} q_{\phi}(z|x_n).\)
因为只有最后一项(交叉熵)和先验分布有关系, 可见, 最优的先验分布\(p_{\lambda}\)就是
\[q(z) = \frac{1}{N} \sum_{n=1}^{N} q_{\phi}(z|x_n).
\]
但是这样的先验分布每一次计算量太大, 所以作者退而求其次, 假设
\[p_{\lambda}(z) = \frac{1}{K} \sum_{k=1}^K q_{\phi}(z|\mu_k),
\]
其中\(\mu_k\)是可训练的参数.
分级的VAE
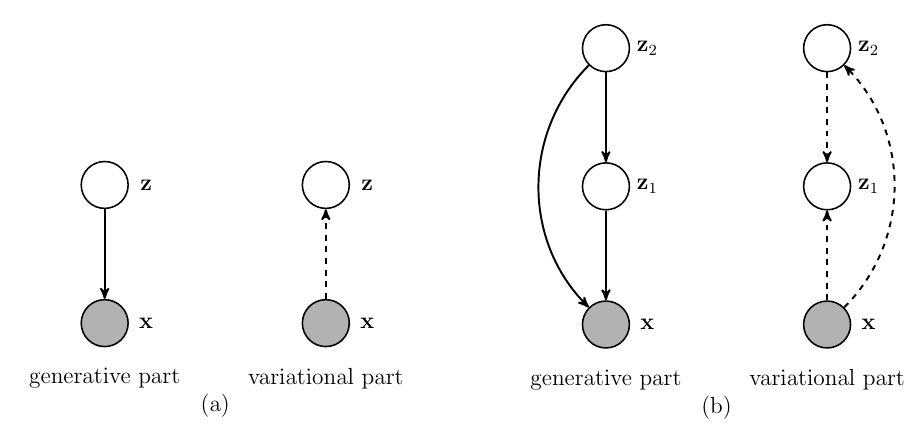
一般的VAE的隐变量往往只有少部分是激活的有效的, 而且这一点越在deep的网络中越容易出现.
所以作者提出了如上图(b)的一种双层的改进方式.
具体的, variational part:
\[q_{\phi}(z_1|x, z_2)q_{\psi}(z_2|x),
\]
generative part:
\[p_{\theta}(x|z_1, z_2) p_{\lambda}(z_1|z_2)p(z_2).
\]
其中:
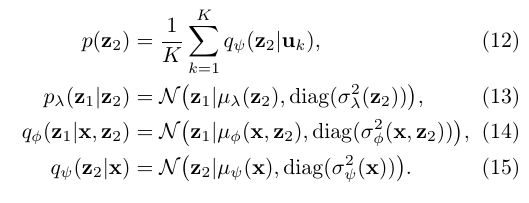
感觉有点残差的味道.


