Hern\(\'{a}\)n M. and Robins J. Causal Inference: What If.
这一章讲一种新的方法: propensity scores.
15.1 Outcome regression
在满足条件可交换性下,
\[\mathbb{E} [Y^{a=1, c=0}|L=l] = \mathbb{E} [Y|A=1, C=0, L=l].
\]
之前的模型都是对等式左端进行建模, 倘若我们对等式右端进行建模呢?
\[\mathbb{E} [Y|A,C=0, L] = \alpha_0 + \alpha_1 A + \alpha_2 AL + \alpha_3L.
\]
15.2 Propensity scores
在IP weighting 和 g-estimation的使用过程中, 我们需要估计条件概率\(\mathrm{Pr}[A=1|L]\), 记为\(\pi (L)\).
\(\pi (L)\) 就是所谓的propensity scores, 其反应了特定\(L\)的一种倾向.
首先我们要证明,
\[Y^a \amalg A | L \Rightarrow Y^a \amalg A | \pi(L).
\]
不妨假设\(\pi(L) = s \Leftrightarrow L \in \{l_i\}\), 则
\[\begin{array}{ll}
\mathrm{Pr}[Y^a|\pi(L)=s]
&= \mathrm{Pr} [Y^a|L \in \{l_i\}] \\
&= \frac{\sum_i\mathrm{Pr}[Y^a,L=l_i]}{\sum_i \mathrm{Pr} [L=l_i]}\\
&= \frac{\sum_i\mathrm{Pr}[Y|A=a, L=l_i]\mathrm{Pr}[L=l_i]}{\sum_i \mathrm{Pr} [L=l_i]}\\
&= \frac{\mathrm{Pr}[A=a|L=l] \cdot \sum_i\mathrm{Pr}[Y|A=a, L=l_i]\mathrm{Pr}[L=l_i]}{\mathrm{Pr}[A=a|L=l]\sum_i \mathrm{Pr} [L=l_i]}\\
&= \frac{\cdot \sum_i\mathrm{Pr}[Y|A=a, L=l_i]\mathrm{Pr}[A=a, L=l_i]}{\sum_i \mathrm{Pr} [A=a, L=l_i]}\\
&= \frac{\cdot \sum_i\mathrm{Pr}[Y, A=a, L=l_i]}{\sum_i \mathrm{Pr} [A=a, L=l_i]}\\
&= \frac{\cdot \mathrm{Pr}[Y, A=a, \pi(L)=s]}{\mathrm{Pr} [A=a, \pi(L)]}\\
&= \mathrm{Pr} [Y|A=a, \pi(L)=s].
\end{array}
\]
注意: \(\pi(l_i) = \pi(l_j) = \pi(l) = s\).
注意到, 上面有很重要的一步, 我们上下同时乘以\(\mathrm{Pr}[A=a|L=l]\), 实际上只有当\(A \in \{0, 1\}\)的时候才能成立, 因为二元, 加之\(\pi(L)=s\), 所以
\[\mathrm{Pr}[A=a|L=l_i] = \mathrm{Pr}[A=a|L=l_j].
\]
也就是说当\(A\)不是二元的时候, 上面的推导就是错误的了.
怪不得书上说, propensity scores这个方法是很难推广的非二元treatments的情况的.
15.3 Propensity stratification and standardization
此时, 我们可以把\(\pi(L)\)看成一个新的中间变量\(L\)(confounder?), 如下图:
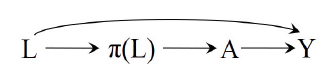
要知道, 原来的\(L\)可能是一个高维向量, 现在压缩为一维, 这意味着我们的可以将
\[\mathbb{E}[Y|A, C=0, \pi(L)]
\]
假设地更加精简.
估计或许更加牢靠(直接无参数模型?).
但是需要指出是, 不同个体的\(\pi(L)\)往往都是不同的, 这就导致我们想要估计
\[\mathbb{E} [Y|A=1, C=0|\pi(L)=s] - \mathbb{E} [Y|A=0, C=0|\pi(L)=s]
\]
几乎是不可能的.
一种比较好的做法是, 分成一段段区间, 考虑
\[\mathbb{E} [Y|A=1, C=0|\pi(L)\in \Delta_s] - \mathbb{E} [Y|A=0, C=0|\pi(L)\in \Delta_s].
\]
比如书上推荐的10分位.
当然这种做法会在一定程度上破化条件可交换性, 但是可以认为如果区间取得比较合适, 结果应该是比较合理的.
另外需要指出的, 我们往往会陷入一个误区, 觉得\(\pi(L)\), 即条件概率\(\mathrm{Pr}[A=1|L]\)的估计越准确越好, 实际上不是.
我们需要保证的仅仅是满足条件可交换性, 实际上准确度无关紧要.
有些时候过分追求准确度会适得其反, 因为这时我们往往会引入很多的变量, 导致我们的条件可交换性被大大破坏了.
所以不要仅仅当成是回归问题来看.
15.4 Propensity matching
看就是就是matching的翻版, 不过我matching也没搞懂哦.
15.5 Propensity models, structural models, predictive models
就主要是15.3里讲过的.
Fine Point
Nuisance parameters
Effect modification and the propensity score
Technical Point
Balancing scores and prognostic scores