Chapter 8 Selection Bias

目录

• 8.1 The structure of selection bias
• 8.2 Examples of selection bias
• 8.3 Selection bias and confounding
• 8.4 Selection bias and censoring
• 8.5 How to adjust for selection bias
• 8.6 Selection without bias
• Fine Point
  • Selection bias in case-control studies
  • The strength and direction of selection bias
• Technical Point
  • THe built-in selection bias of hazard bias
  • Multiplicative survival model

Hern\(\'{a}\)n M. and Robins J. Causal Inference: What If.

上一章讲了confounding, 这种bias来源于treatment和outcome受同一个未观测的cause影响, 但是这种bias在随机实验中可以避免.
这一章要讲的试selection bias, 即便是在随机试验中, 也无法避免.

8.1 The structure of selection bias

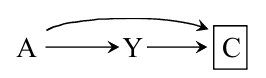
这里, 作者给出了一个非常好的例子, 如上图所示:
\(A \in \{0, 1\}\) 表示是否注射叶酸, 而\(Y \in \{0, 1\}\) 表示胎儿是否心脏畸形, 而\(C \in \{0, 1\}\)则表示是否死亡.

这里, 虽然是否注射叶酸, 我们是随机选择的, 但是在实际调查中, 只有顺利出生(\(C=0\))的才会被记录是否心脏畸形.
所以, 我们必须在\(C=0\)的条件下估计causal effect.
但是注意到, \(A\)存在指向\(C\)的箭头(即\(A=1\)会降低死亡的风险).
此时, \(Y^a\)和\(A\)在给定\(C=1\)的条件下并不独立.
这就是本章讲的selection bias.

8.2 Examples of selection bias

8.3 Selection bias and confounding

8.4 Selection bias and censoring

虽然我们只有\(C=0\)的情况, 我们可以把\(C\)也看出一个treatment, 则我们只需要关注

\[Y^{a, c=0}, \]

即可.

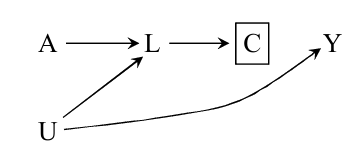
8.5 How to adjust for selection bias

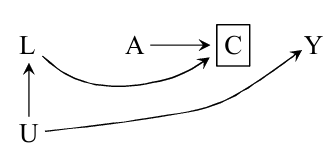
如何计算\(\mathbb{E}[Y^{a, c=0}]\), 这一节给出的是一种特殊的IP weighting的方法, 说实话没怎么看懂, 这里以上图为例给出我自己的理解.

\[\mathbb{E}[\frac{I(A=a, C=0)Y}{f(C|A,L)}] \\ = \sum_l \sum_y \frac{I(A=a, C=0)Y}{f(C=0|A=a,L=l)} \mathrm{Pr}[Y|a,c,l] \mathrm{Pr}[C=0|a,l] \mathrm{Pr}[A=a, L=l] \\ = \sum_l \sum_y I(A=a, C=0)Y^{a,0} \mathrm{Pr}[Y^{a,0}|l] \mathrm{Pr}[A=a, L=l] \\ = \mathbb{E} [Y^{a, c=0}] \mathrm{Pr}[A=a]. \]

其实, 个人感觉如果是

\[\mathbb{E}[\frac{I(A=a, C=0)Y}{f(C,A|L)}] , \]

就直接可以得出结果了.

8.6 Selection without bias

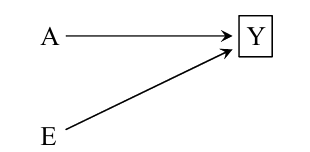
这一节讲了给定\(Y\)的情况下, \(A, E\)产生关联的不同情况.

Fine Point

Selection bias in case-control studies

The strength and direction of selection bias

Technical Point

THe built-in selection bias of hazard bias

Multiplicative survival model

\[\mathrm{Pr}[Y=0|E=e, A=a] = g(e)h(a), \\ \mathrm{Pr}[Y=1|E=e, A=a] = 1 - g(e)h(a). \\ \]