Chapter 6 Graphical Representation of Causal Effects

目录

• 6.1 Causal diagrams
• 6.2 Causal diagrams and marginal independence
• 6.3 Causal diagrams and conditional independence
• 6.4 Positivity and consistency in causal diagrams
• 6.5 A structural classification of bias
• 6.6 The structure of effect modification
• Fine Point
  • D-separation
  • Faithfulness
• Technical Point
  • Causal directed acyclic graphs
  • Counterfactual models associated with a causal DAG

Hern\(\'{a}\)n M. and Robins J. Causal Inference: What If.

本章引入有向无环图(CAG)来表述因果推断模型.

6.1 Causal diagrams

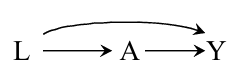
正如上图所示, 因果推断的模型可以用一个有向无环图表示, 如两个变量有直接的连接, 比如\(A \rightarrow Y\), 则表示\(A\)关于\(Y\)存在直接的causal effect, 否则表示不存在直接的causal effect.
当然, 不存在causation并不表示不存在association.

上图表示, \(Y\)受到两个intervention的影响, 同时\(A\)受到\(L\)影响, 所以:

\[Y^{e, a} = Y^{e, A^e}. \]

6.2 Causal diagrams and marginal independence

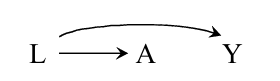
又如上图所示, 由于\(A, Y\)之间没有直接的指向, 所以我们可以断定

\[\mathrm{Pr} [Y^{a=1}=1] = \mathrm{Pr} [Y^{a=0}=1]. \]

但是, 一般来说\(A, Y\)是相关联的, 也就是非独立的.

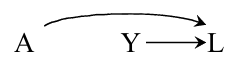
在另一种情况下, \(A, Y\)之间既没有causation, 也没有association.
这个还是得看technical point啊.

6.3 Causal diagrams and conditional independence

这一节就是讨论在\(L\)已知的情况下的条件独立性.

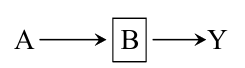
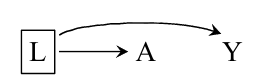
显然这两种情况下, \(A, Y\)是条件独立的, 因为知道了\(A\)不会对\(Y\)的预测有任何的影响.

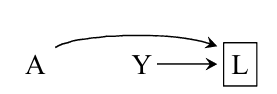
这第三种, \(A, Y\)很有可能是条件相关的, 具体还是看原文的例子的解释吧.

6.4 Positivity and consistency in causal diagrams

6.5 A structural classification of bias

这一节主要讲一些偏置, 即什么时候能够准确地计算出causal effect, 有了图模型比较方便说明.

6.6 The structure of effect modification

Fine Point

D-separation

Faithfulness

我们知道\(A, Y|L\)是独立的, 这在causal DAG的马尔可夫性条件下可以推出, faithfulness 就是假设, 当\(A, Y|L\)是独立的时候, \(A, Y|L\)是D-separation的.

Technical Point

Causal directed acyclic graphs

Causal DAG:

1. 倘若节点\(V_j\)没有直接指向\(V_m\), 则表明\(V_j\)关于\(V_m\)没有直接的causal effect;

2. 如果有cause同时作用在两个变量上, 即使该cause没有被观测, 也应该在Causal DAG图中表示出来;

3. 任何变量都是其后代的一个cause.

另外, 针对\(v=(v_1, v_2,\cdots, v_n)\), 假设其满足马尔科夫性, 即

\[f(v) = \prod f(v_j | pa_j), \]

其中\(pa_j\)是\(v_j\)的直接父节点.

Counterfactual models associated with a causal DAG

为了将二者联系起来, 首先我们要给出模型假设(NPSEM):

\[V_m^{\bar{v}_{m-1}} \equiv V_m^{pa_m} = f_m(pa_m, \epsilon_m). \]

NPSEM-IE:

\[\epsilon_i, \epsilon_j, i \not = j. \]

FFRCISTGs:
\(V_m^{\bar{v}_{m-1}} = f_m(pa_m, \epsilon_m)\) 与 所有\(V_j^{\bar{v}_{j-1}}=f_j(pa_j, \epsilon_j), j < m\)(且 \(\bar{v}_{j-1}\) 是 \(\bar{v}_{m-1}\)的子集) 联合独立.

上面任一条件我们都能推出马尔科夫性, 以及一些我们需要的可交换性.