Intriguing Properties of Contrastive Losses

目录

• 概
• 主要内容
  • 广义对比损失
    • 不同的先验
    • 不同的权重比\(\tau, \lambda\)
  • Feature Suppression
  • DigitOnImageNet dataset
  • RandBit dataset
• 代码

[Chen T. & Li L. Intriguing Properties of Contrastive Losses. arXiv preprint arXiv 2011.02803, 2020.]

概

普通的对比损失有一种广义的表示方法, 改变alignment和distribution项的权重比有何影响? 同时, 改用不同的先验分布会有什么影响?

另外作者还发现了一种特征压制的现象, 即对比损失会更容易抓住一些简单的特征(如果存在), 而忽视不易往往更为有效的特征, 且这种现象不会随着网络的大小, 训练的次数或者batch size等等因素变化而产生明显变化.

主要内容

广义对比损失

普通的对比损失

\[\mathcal{L} = -\frac{1}{n} \sum_{i, j \in \mathcal{MB}} \log \frac{\exp (\mathrm{sim}(z_i, z_j) / \tau)}{\sum_{k=1}^{2n} \mathbf{1}_{[k \not= i]}\exp (\mathrm{sim}(z_i, z_k) / \tau)}, \]

广义的对比损失

\[\mathcal{L} = -\frac{1}{n} \sum_{i, j} \mathrm{sim}(z_i, z_j) + \lambda \cdot \frac{1}{n} \sum_{i} \log \sum_{k=1}^{2n} \mathbf{1}_{k \not = i} \exp (\mathrm{sim} (z_i, z_k) / \tau). \]

第一项为\(\mathcal{L}_{alignment}\), 第二项为\(\mathcal{L}_{distribution}\), 第一项会使得正样本之间靠近, 第二项使得负样本之间趋于一个先验分布, 普通的对比损失是以均匀分布为先验的(直观上这种情况下的熵最大). 从互信息的角度来理解:

\[I(X;Y) = H(X) - H(X|Y), \]

\(H(X)\)对应\(\mathcal{L}_{distribution}\), \(-H(X|Y)\)对应\(\mathcal{L}_{alignment}\).

不同的先验

作者首先研究了不同的先验分布会有什么影响(其算法涉及到sliced wasserstein distance, 暂时不想了解):

如下图所示, 在CIFAR-10上差距不大, ImageNet上当projection head只有两层的时候有差距但是增加到三层的时候又没啥差距了.

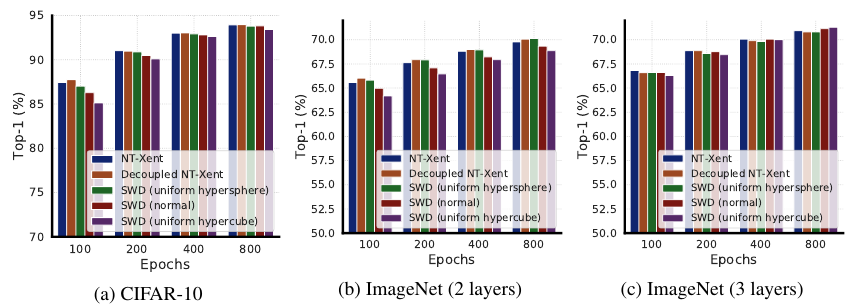
不同的权重比\(\tau, \lambda\)

现在广义对比损失上有两个我们可以调节的参数, 包括temperature \(\tau\)和\(\lambda\).

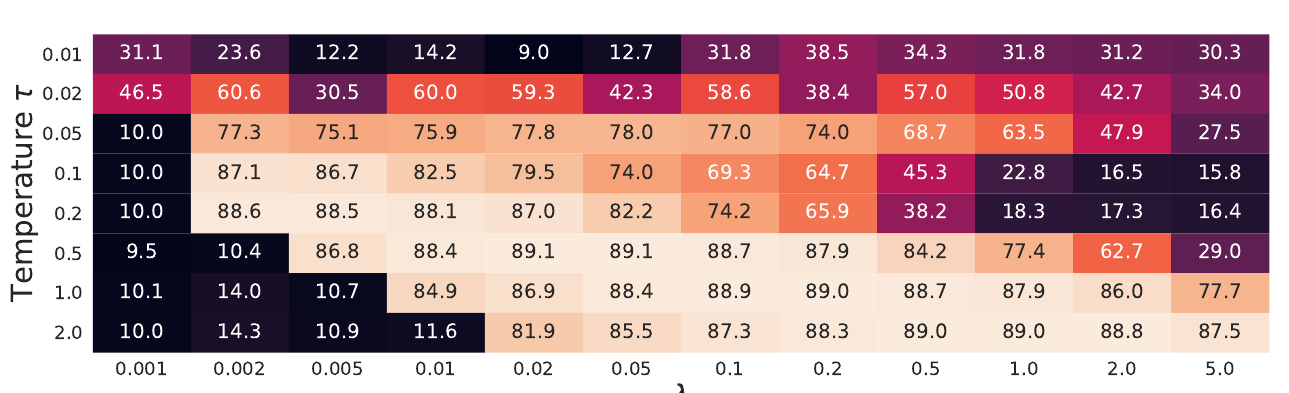
如上图所示, 作者称二者的关系是相反的, 即较大的\(\tau\)往往需要较小的\(\lambda\), 较小的\(\tau\)往往需要较大的\(\lambda\).

Feature Suppression

作者发现比较简单的特征更容易被学习到, 且该部分特征会阻碍网络学习其他的更加复杂的特征.

DigitOnImageNet dataset

第一个实验是, 在一些图片上加上一些数字:

注: 这些数字是在augmentation之前加的, 也就是说正样本之间是会共享这部分数字信息的.

用这个数据集在

1. 监督学习

   

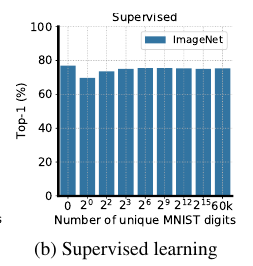
2. 对比学习, 并且变换\(\tau\)

   

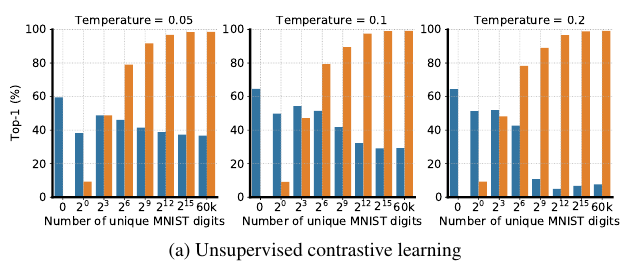
可以发现, 这部分共享信息对于有监督训练分类网络(关于Imagenet)是几乎没有影响的. 但是在对比学习中, 随着数字的量的增加, 提取到的特征大部分是用于分类数字而不是占据更多共享信息的图片. 虽然小一点的\(\tau\)能够在一定程度上缓解这一状况. 这说明, 对比学习很容易被一些小的简单的共享信息所误导, 去学习一些简单的特征, 而且这些特征会阻碍进一步学习更复杂的特征.

RandBit dataset

这部分实验进一步说明, 这些简单特征甚至能够完全抹杀复杂的特征.

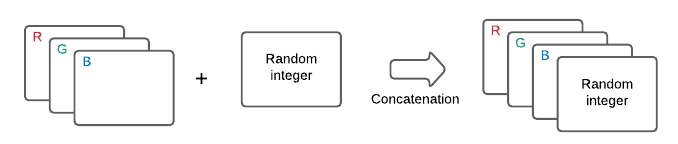
这部分数据集的构造方式是, 对普通的RGB图片添加新的channels, 每一层channel要么都是\(1\), 要么都是\(0\)（看代码似乎是这个意思, 不过此时共享的信息应该是\(n\)?).

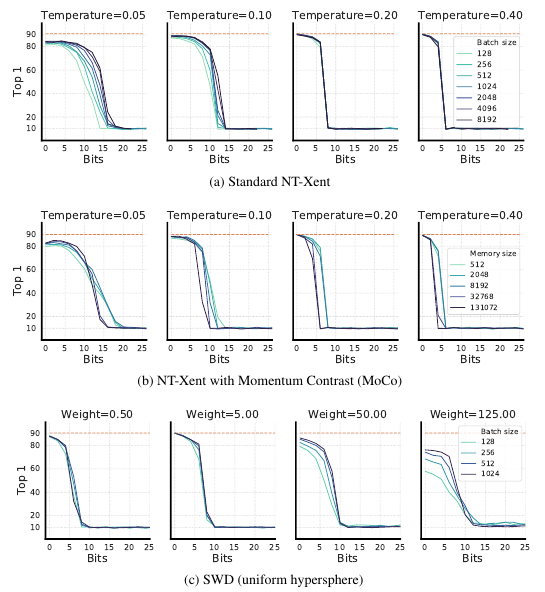
结果如上图, 可以发现, 这一点点的几个bits的共享的信息就能够使得对比损失效果骤降甚至是完全失效, 且改变\(\tau\), batch size, 或者是先验分布, 以及训练的框架都不能有所改善.

代码

原文代码