Generating Adversarial Examples with Adversarial Networks
@article{xiao2018generating,
title={Generating Adversarial Examples with Adversarial Networks},
author={Xiao, Chaowei and Li, Bo and Zhu, Junyan and He, Warren and Liu, Mingyan and Song, Dawn},
journal={arXiv: Cryptography and Security},
year={2018}}
概
本文利用GAN生成adversarial samples.
主要内容
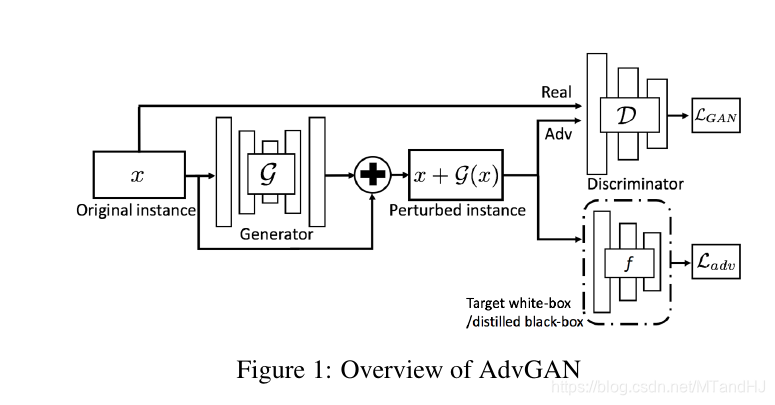
其中\(\mathcal{G}\)是生成器, \(\mathcal{D}\)是用于判别真假的判别器, 二者都是需要训练的, 而\(f\)是已知的我们需要攻击的模型(在white-box下是不需要训练的).
训练判别器很普通的GAN是类似的, 即最大化下式:
\[\tag{1}
\mathcal{L}_{GAN} = \mathbb{E}_{x} \log \mathcal{D}(x) + \mathbb{E}_{x} \log (1-\mathcal{D}(x+\mathcal{G}(x))).
\]
训练生成器, 除了\(\mathcal{L}_{GAN}\), 还需要
\[\tag{2}
\mathcal{L}_{adv}^f = \mathbb{E}_x \ell_f (x+\mathcal{G}(x),t),
\]
其中\(t\)是我们所需要的攻击目标(注意这里通过对\(\ell\)的一些额外的选择, 是可以用到untargeted attack的).
\[\tag{3}
\mathcal{L}_{hinge} = \mathbb{E}_x \max (0, \|\mathcal{G}(x)\|_2 -c),
\]
显然(3)是保证摄动不要太大.
所以训练生成器是最小化
\[\tag{4}
\mathcal{L}=\mathcal{L}_{adv}^f+ \alpha \mathcal{L}_{GAN} + \beta \mathcal{L}_{hinge}.
\]
black-box 拓展
该方法可以拓展到black-box上, 假设\(b(x)\)是目标网络, 其结构和训练数据都是未知的, 此时我们构建一个替代网络\(f(x)\)用于逼近\(b(x)\). 利用交替训练, 更新生成器\(\mathcal{G}\)和\(f\).
- 固定\(f_{i-1}\), 更新\(\mathcal{G}_i\): \(\mathcal{G}_i\)初始化参数为\(\mathcal{G}_{i-1}\), 则
\[\mathcal{G}_i, \mathcal{D}_i = \arg \min _{\mathcal{G}} \max_{\mathcal{D}} \mathcal{L}_{adv}^f+ \alpha \mathcal{L}_{GAN} + \beta \mathcal{L}_{hinge}.
\]
- 固定\(\mathcal{G}_i\), 更新\(f_i\): 初始化\(f_i\)的参数为\(f_{i-1}\), 则
\[f_i=\arg \min_f \mathbb{E}_x \mathcal{H} (f(x), b(x)) + \mathbb{E}_x \mathcal{H} (f(x+\mathcal{G}_i(x)), b(x+\mathcal{G}_i(x))).
\]
其中\(\mathcal{H}\)表示交叉熵损失.
