McGan: Mean and Covariance Feature Matching GAN
@article{mroueh2017mcgan:,
title={McGan: Mean and Covariance Feature Matching GAN},
author={Mroueh, Youssef and Sercu, Tom and Goel, Vaibhava},
journal={arXiv: Learning},
year={2017}}
概
利用均值和协方差构建IPM, 获得相应的mean GAN 和 covariance gan.
主要内容
IPM:
\[d_{\mathscr{F}} (\mathbb{P}, \mathbb{Q}) = \sup_{f \in \mathscr{F}} |\mathbb{E}_{x \sim \mathbb{P}} f(x) - \mathbb{E}_{x \sim \mathbb{Q}} f(x)|.
\]
当\(\mathscr{F}\)是对称空间, 即\(f \in \mathscr{F} \rightarrow - f \in \mathscr{F}\),可得
\[d_{\mathscr{F}} (\mathbb{P}, \mathbb{Q}) = \sup_{f \in \mathscr{F}} \big \{\mathbb{E}_{x \sim \mathbb{P}} f(x) - \mathbb{E}_{x \sim \mathbb{Q}} f(x) \big\}.
\]
Mean Matching IPM
\[\mathscr{F}_{v,w,p}:= \{f(x)=\langle v, \Phi_w(x) \rangle | v\in \mathbb{R}^m, \|v\|_p \le 1, \Phi_w:\mathcal{X} \rightarrow \mathbb{R}^m, w \in \Omega\},
\]
其中\(\|\cdot \|_p\)表示\(\ell_p\)范数, \(\Phi_w\)往往用网络来表示, 我们可通过截断\(w\)来使得\(\mathscr{F}_{v,w,p}\)为有界线性函数空间(有界从而使得后面推导中\(\sup\)成为\(\max\)).
其中
\[\mu_w(\mathbb{P})= \mathbb{E}_{x \sim \mathbb{P}} [\Phi_w(x)] \in \mathbb{R}^m.
\]
最后一个等式的成立是因为:
\[\|x\|_* = \max \{\langle v, x \rangle | \|v\| \le 1\},
\]
又\(\| \cdot \|_p\)的对偶范数是\(\|\cdot\|_q, \frac{1}{p}+\frac{1}{q}=1\).
prime
整个GAN的训练过程即为
\[\tag{3}
\min_{g_\theta} \max_{w \in \Omega} \max_{v, \|v\|_p \le 1} \mathscr{L}_{\mu} (v,w,\theta),
\]
其中
\[\mathscr{L}_{\mu} (v,w,\theta) = \langle v, \mathbb{E}_{x \in \mathbb{P}_r} \Phi_w(x) - \mathbb{E}_{z \sim p(z)} \Phi_w(g_{\theta} (z)) \rangle.
\]
估计形式为
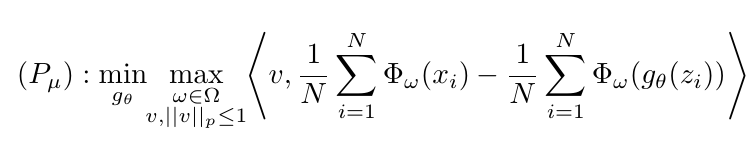
dual
也有对应的dual形态
\[\tag{4}
\min_{g_\theta} \max_{w \in \Omega} \|\mu_w(\mathbb{P}_r) - \mu_w (\mathbb{P}_{\theta})\|_q.
\]
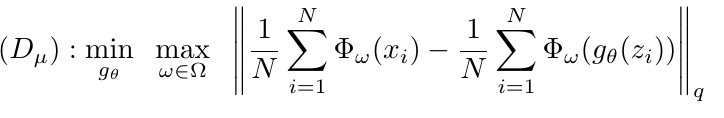
Covariance Feature Matching IPM
\[\mathscr{F}_{U, V,w} := \{f(x)= \sum_{j=1}^k \langle u_j, \Phi_w(x) \rangle \langle v_j, \Phi_w(x)\rangle, \langle u_i, u_j \rangle = \langle v_i, v_j \rangle =0, i \not = j, else \:1 \},
\]
等价于
\[\mathscr{F}_{U, V,w} := \{f(x)= \langle U^T \Phi_w(x), V^T\Phi_w(x) \rangle, U^TU=I_k, V^TV=I_k, w \in \Omega \}.
\]
并有
其中\([A]_k\)表示\(A\)的\(k\)阶近似, 如果\(A = \sum_i \sigma_iu_iv_i^T\), \(\sigma_1\ge \sigma_2,\ldots\), 则\([A]_k=\sum_{i=1}^k \sigma_i u_iv_i^T\). \(\mathcal{O}_{m,k} := \{M \in \mathbb{R}^{m \times k} | M^TM = I_k \}\), \(\|A\|_*=\sum_i \sigma_i\)表示算子范数.
prime
\[\tag{6}
\min_{g_\theta} \max_{w \in \Omega} \max_{U,V \in \mathcal{P}_{m, k}} \mathscr{L}_{\sigma} (U, V,w,\theta),
\]
其中
\[\mathscr{L}_{\sigma} (U,V,w,\theta) = \mathbb{E}_{x \sim \mathbb{P}_r} \langle U^T \Phi_w(x), V^T\Phi_w(x) \rangle- \mathbb{E}_{z \sim p_z} \langle U^T \Phi_w(g_{\theta}(z)), V^T\Phi_w(g_{\theta}(z)) \rangle.
\]
采用下式估计
dual
\[\tag{7}
\min_{g_{\theta}} \max_{w \in \Omega} \| [\Sigma_w(\mathbb{P}_r) - \Sigma_w(\mathbb{P}_{\theta})]_k\|_*.
\]
注: 既然\(\Sigma_w(\mathbb{P}_r) - \Sigma_w(\mathbb{P}_{\theta})\)是对称的, 为什么\(U \not =V\)? 因为虽然其对称, 但是并不(半)正定, 所以\(v_i=-u_i\)也是有可能的.
算法
代码
未经测试.
import torch
import torch.nn as nn
from torch.nn.functional import relu
from collections.abc import Callable
def preset(**kwargs):
def decorator(func):
def wrapper(*args, **nkwargs):
nkwargs.update(kwargs)
return func(*args, **nkwargs)
wrapper.__doc__ = func.__doc__
wrapper.__name__ = func.__name__
return wrapper
return decorator
class Meanmatch(nn.Module):
def __init__(self, p, dim, dual=False, prj='l2'):
super(Meanmatch, self).__init__()
self.norm = p
self.dual = dual
if dual:
self.dualnorm = self.norm
else:
self.init_weights(dim)
self.projection = self.proj(prj)
@property
def dualnorm(self):
return self.__dualnorm
@dualnorm.setter
def dualnorm(self, norm):
if norm == 'inf':
norm = float('inf')
elif not isinstance(norm, float):
raise ValueError("Invalid norm")
p = 1 / (1 - 1 / norm)
self.__dualnorm = preset(p=p, dim=1)(torch.norm)
def init_weights(self, dim):
self.weights = nn.Parameter(torch.rand((1, dim)),
requires_grad=True)
@staticmethod
def _proj1(x):
u = x.max()
if u <= 1.:
return x
l = 0.
c = (u + l) / 2
while (u - l) > 1e-4:
r = relu(x - c).sum()
if r > 1.:
l = c
else:
u = c
c = (u + l) / 2
return relu(x - c)
@staticmethod
def _proj2(x):
return x / torch.norm(x)
@staticmethod
def _proj3(x):
return x / torch.max(x)
def proj(self, prj):
if prj == "l1":
return self._proj1
elif prj == "l2":
return self._proj2
elif prj == "linf":
return self._proj3
else:
assert isinstance(prj, Callable), "Invalid prj"
return prj
def forward(self, real, fake):
temp = (real - fake).mean(dim=1)
if self.dual:
return self.dualnorm(temp)
elif not self.training and self.dual:
raise TypeError("just for training...")
else:
self.weights.data = self.projection(self.weights.data) #some diff here!!!!!!!!!!
return self.weights @ temp
class Covmatch(nn.Module):
def __init__(self, dim, k):
super(Covmatch, self).__init__()
self.init_weights(dim, k)
def init_weights(self, dim, k):
temp1 = torch.rand((dim, k))
temp2 = torch.rand((dim, k))
self.U = nn.Parameter(temp1, requires_grad=True)
self.V = nn.Parameter(temp2, requires_grad=True)
def qr(self, w):
q, r = torch.qr(w)
sign = r.diag().sign()
return q * sign
def update_weights(self):
self.U.data = self.qr(self.U.data)
self.V.data = self.qr(self.V.data)
def forward(self, real, fake):
self.update_weights()
temp1 = real @ self.U
temp2 = real @ self.V
temp3 = fake @ self.U
temp4 = fake @ self.V
part1 = torch.trace(temp1 @ temp2.t()).mean()
part2 = torch.trace(temp3 @ temp4.t()).mean()
return part1 - part2
