Deep Linear Networks with Arbitrary Loss: All Local Minima Are Global
问题
这篇文章是关于深度学习的一些理论分析.
假设这么一个网络:
其中是输入,是第层的权重,而是最后的输出. 没错,这篇文章研究的是深度线性网络的性质(没有激活函数). 当然,这样子,无论有多少层,这个网络最后是一个普通线性函数,所以,作者的本意应该只是借此来窥探深度学习的一些性质.
作者证明了,在满足一定条件下,这个深度线性网络,任何局部最优解都是全局最优解.
假设和重要结果
损失函数如此表示:
假设
- 表示第层的神经元个数,即表示输入层的维度,, 表示输出层的维度,
- ,
- 损失函数关于凸且可微.
定理1:满足上面假设的深度线性网络,任意局部最优都是全局最优.
考虑下面问题p(2):
并记.
则:
定理3:
假设是任意的可微函数,且满足:
则关于p(2)的任意的极小值点,都将满足:
证明
注意到, 可表示成:
则是关于的凸的可微函数(注意是关于), 所以,当的时候,便是,即得最小值点. 这意味着,只要我们证明了定理3,也就证明了定理1.
下证定理3:
首先定义:
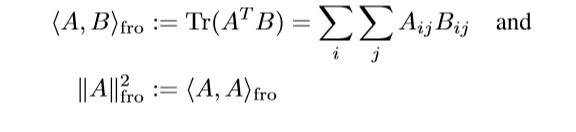
记:
容易证明(这部分论文中也给出了证明,不在此贴出):
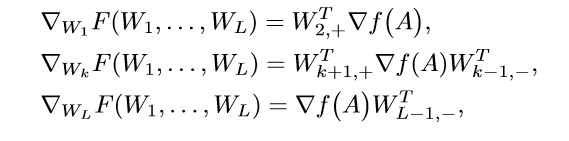
其中:
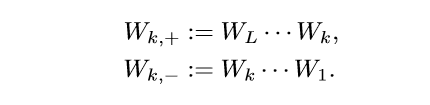
不失一般性,假设, 因为令:
则,定义在之上,且使得为极小值,当且仅当使得为极小值,所以的地位是相同的,我们可以直接假设.
是最小值点,则存在, 使得满足:
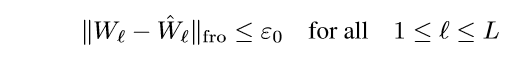
的点满足:
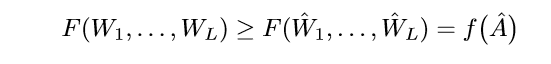
于是:
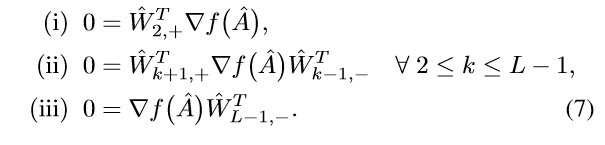
当的时候:
于是只要证明, 的时候,上式也成立即可.
我们的想法是构造一族极小值点, 满足:
通过一些性质,推出.
首先证明,满足:
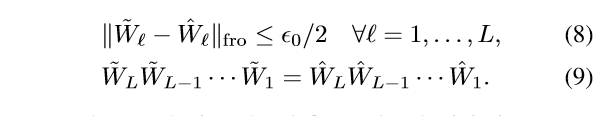
的点都是极小值点.
因为:
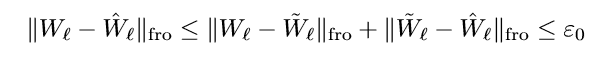
所以:
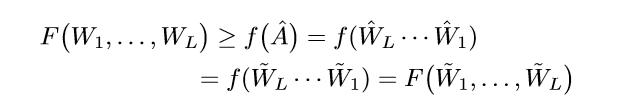
所以也是一个极小值点.
那么如何来构造呢?
可知:
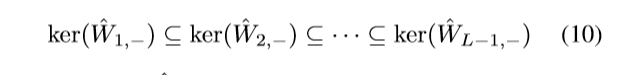
对进行奇异值分解:
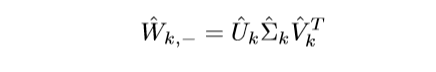
因为, 所以其分解是这样的:
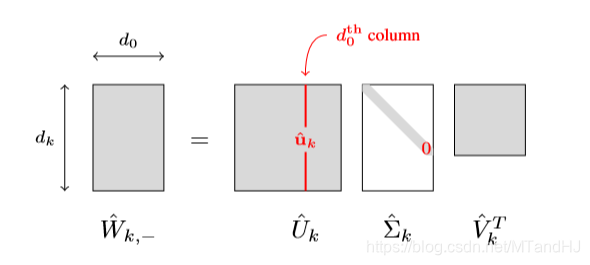
注意到,这里体现了为什么需要, 否则不可能等于(因为其秩永远小于).
假设是第一个的,则下面的构造便是我们所需要的:

其中表示奇异值分解的列, 很明显,满足.
条件(8)容易证明,用数学归纳法证明(9):
第一项成立,假设第项也成立, 于是

也成立,所以条件成立.
既然满足其构造方式的所有点都是点都是极小值点,那么:
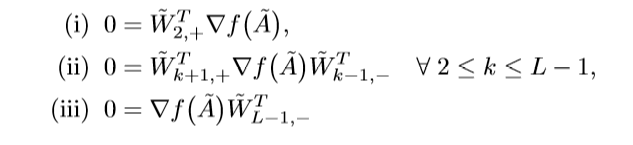
注意,对所有的满足条件的都成立.
的时候可得:
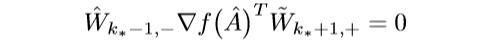
又, 所以:
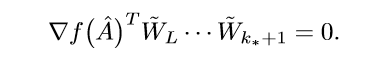
注意到的时候,也有上面的形式.
首先,令, 则, 于是:
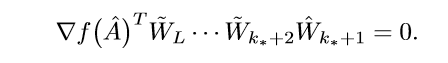
在去任意, 与上式作差可得:
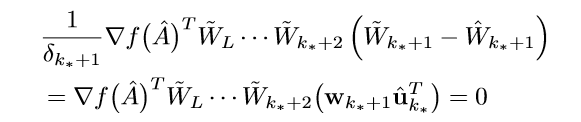
俩边同乘上可得:
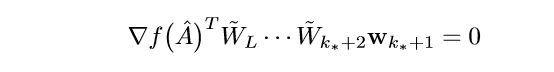
因为是任意的,所以,左端为0,以此类推,最后可得:
证毕.
注
我没有把定理2放上来.
有一个方向,定理3中的极小值点改成极大值点,似乎定理也成立,即:
假设是任意的可微函数,且满足:
则关于p(2)的任意的极大值点,都将满足:
我自己仿照论文的证明是可以证明出来的,不过,既然, 那么依然是的最小值点,是不是可以这么认为,压根没有存粹的极大值点.
另外作者指出,极小值点不能改为驻点,因为便是一个驻点,但是没有必须为0的规定.
此外作者还说明了,为什么要可微等等原因,详情回见论文.




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 智能桌面机器人:用.NET IoT库控制舵机并多方法播放表情
· Linux glibc自带哈希表的用例及性能测试
· 深入理解 Mybatis 分库分表执行原理
· 如何打造一个高并发系统?
· .NET Core GC压缩(compact_phase)底层原理浅谈
· 手把手教你在本地部署DeepSeek R1,搭建web-ui ,建议收藏!
· 新年开篇:在本地部署DeepSeek大模型实现联网增强的AI应用
· Janus Pro:DeepSeek 开源革新,多模态 AI 的未来
· 互联网不景气了那就玩玩嵌入式吧,用纯.NET开发并制作一个智能桌面机器人(三):用.NET IoT库
· 【非技术】说说2024年我都干了些啥