Dimension reduction in principal component analysis for trees

目录

• 问题
• 重要的定义
  • 距离
  • 支撑树 交树
  • 序
  • tree-line
  • path
  • $L_i^f, L_i^b$
  • 重要的性质
• 其它

Alfaro C A, Aydin B, Valencia C E, et al. Dimension reduction in principal component analysis for trees[J]. Computational Statistics & Data Analysis, 2014: 157-179.

Aydin B, Pataki G, Wang H, et al. A principal component analysis for trees[J]. The Annals of Applied Statistics, 2009, 3(4): 1597-1615.

Wang H, Marron J S. Object oriented data analysis: Sets of trees[J]. Annals of Statistics, 2007, 35(5): 1849-1873.

主要看了第一篇文章，第三篇也就是最开始的那篇的文章并没有细看(主要是有好多看不懂).

问题

PCA主要解决的是欧式空间中的问题，虽然kernel可以将其扩展到高维和非线性. 有一些数据，并不位于欧式空间之中，比如这三篇文章所重视的树形结构的数据，如何抓住这些数据的主干(拓扑结构？)是一个十分有趣的问题.

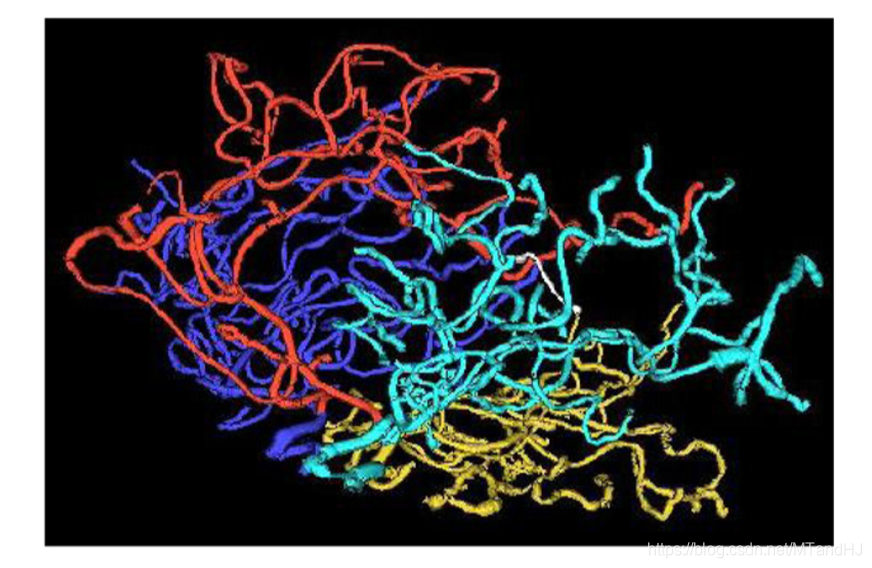
上图即为一种可以表示为树形结构的数据——血管，血管汇集处可以视为是一个树节点，当然树形数据会丢失很多细节，比如血管的粗细，长度等. 但是，因为这里我们只关注血管的拓扑结构(以后用结构代替，因为对拓扑不是很熟悉，用起这个词来总感觉心慌慌的)， 所以我树形结构已经足够了.

现在再一次复述一遍我们的问题:

假设我们有数据集$\mathcal{T}=\{t_i\}$, 每一个$t_i$即为一个树形结构的数据，我们希望找到一棵树或者一类树，使得其能抓住$\mathcal{T}$的主要结构.

很自然的一个问题是，因为不是在欧式空间中，我们无法利用距离来度量俩棵树之间的差距，所以我们首先需要一些定义.

重要的定义

距离

假设有俩棵树$t_1,t_2$, 定义其距离为:

$$d(t_1, t_2) = |t_1\setminus t_2| + |t_2 \setminus t_1|$$

其中$|\cdot|$表示集合的基数，即有限集合内元素的个数.
距离需要满足下面三个性质:

$$d(t_1, t_2) = 0 \Leftrightarrow t_1=t_2, \\ d(t_1, t_2) = d(t_2, t_1) \ge 0, \\ d(t_1, t_3) \le d(t_1, t_2) + d(t_2, t_3).$$

只需证明第三个性质:
$t_1, t_2, t_3$都可以拆分成四份，以$t_1$为例，$t_{11}$只属于$t_1$, $t_{12}$属于$t_1, t_2$但不属于$t_3$， 类似有$t_{13}$, 最后是$t_{123}$属于三者，那么:

$$d(t_1, t_3)= |t_{11}|+|t_{33}| + |t_{12}| + |t_{32}| \\ d(t_2, t_3)=|t_{22}|+|t_{33}| + |t_{21}| + |t_{31}| \\ d(t_1, t_2) = |t_{11}|+|t_{22}| + |t_{13}| + |t_{23}|$$

比较便得证.

支撑树 交树

$Supp(\mathcal{T})=\cup_{i=1}^n t_i$, $Int(\mathcal{T})=\cap_{i=1}^nt_i$.

序

序，起着相当重要的作用，因为序相当于给$t$里面的元素进行了区分，如此我们才能对不同的树进行比较.

这篇文章的序是如此定义的:

1. 根节点为0
2. 假设所有节点的子孙数不超过$k$， 则第$i$个节点的第$j$个子孙序为$ki+j$.

容易证明，一棵树不会出现相同的序.

需要说明的子孙的排序，下面是文章中的一个例子:

这里$k=4$，但是有些时候有点出乎意料:

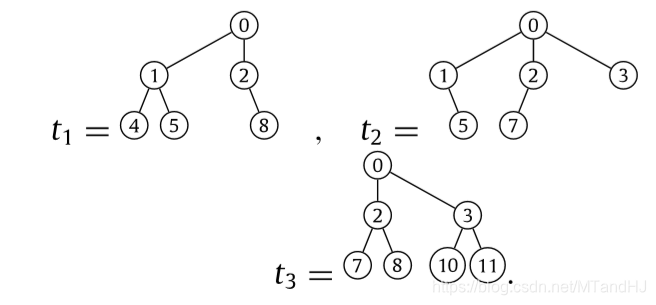
光看规则，$t_2$的5应该为4更加合适，但是因为文章关注的是结构，所以其认为5在右边，所以为5. 事实上这样比较合适，否则支撑树的构造就显得不合理了(因为不同的结构会有相同的序).

这也带来一个问题，如何安排，这些节点的位置，在另外一篇文章中有提及:

虽然觉得如此也并不靠谱，但是似乎也只有如此.

tree-line

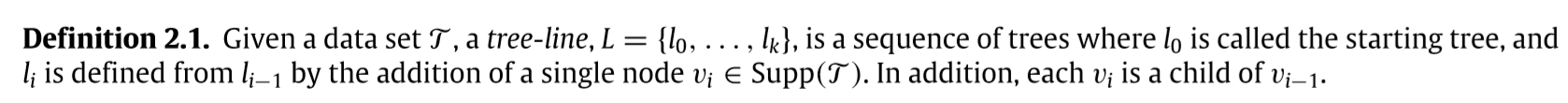
下面的例子，接上面的$t_1, t_2, t_3$:

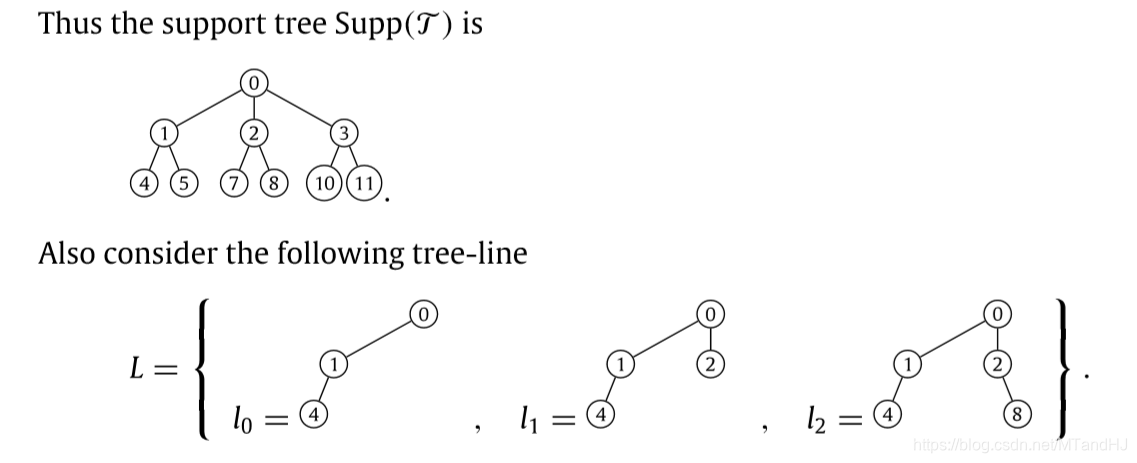
$L$中的$l_0$是预先给定的，给定方式有很多种，比如$Int(\mathcal{T})$等，注意到后面的添加2为0的后代，8为2的后代，所以相应的$0-2-7$等等也是可以的. 不必再往下扩展的原因是支撑树中没有相应的元素了.

$t_1, t_2, t_3$到$L$的距离为:

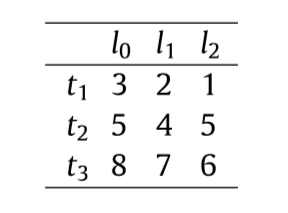
如果我们有$L_1, L_2$俩条tree_lines, 我们可以定义:

$$L_1 \cup L_2 = \{l_{1,i} \cup l_{2,j} | l_{1, i} \in L_1, l_{2, j} \in L_2\},$$

我认为这是很有意思的一点，虽然可能不太高明，但是这就和欧式空间中的子空间类似了(虽然我们非常愚蠢地把子空间中的元素都表示了出来).

有了这个，我们利用距离就可以定义投影了:

$$P_{L_1 \cup L_2}(t)=\mathop{\mathrm{argmin}} \limits_{l \in L_1 \cup L_2} \{d(t, l)\}.$$

我看到这的时候，觉得，有点粗暴，但是不错.

相应的$L_1, L_2, \ldots$也可以如此定义.

接下来有一个引理，这个引理有助于后面的分析，在此之前还需要定义path.

path

对于支撑树，从头节点到叶节点的每条路径均为一个path, 我们以$\mathcal{P}$来表示所有的path(除$l_0$之外), 显然每一条tree-line都可以用$l_0\cup p, p\in \mathcal{P}$来表示.

$L_i^f, L_i^b$

实际上$L_k^f$就是通过前向PCA所求得第k个的"载荷向量", 我认为这个定义是很自然的.

相应的还有后向的:

前向的方法，就是求我们所需要的成分，而后向的方法，就是求我们所舍弃的成分.

重要的性质

我会简单说明证明思路，细节回看论文.

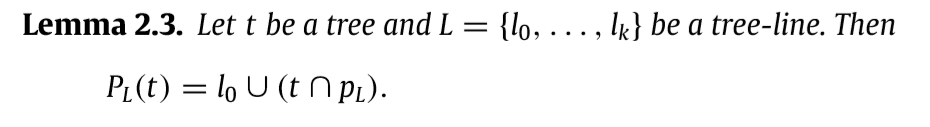
因为$L=l_0 \cup p_L$, 所以我们只需要考虑$t$和$p_L$即可，显然$t \cap p_L$是最合适的，否则，多一个点，$|p_L \backslash t|$会多1， 如果少一个点$|t \backslash p_L|$会多1.

这里我是这么思考的，假设$L_1, \ldots, L_q$互不相同(如果相同，则退化为不同), 则我们只需要考虑$p_{L_1}, \ldots, p_{L_q}$, 上面所说的依然成立，只是增加的量为0或者1，但是不改变此时到达最小的事实.

定义权重:

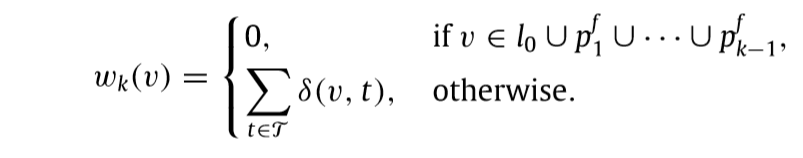
其中$\delta (v,t)=1, v\in t$.
有前向算法:

和相应的定理:

即按照上面的算法，我们可以求出相应的$L_k^f$.
这个算法可以这么理解:
我们的目标是找到以个tree_line， 使得树在其上(加上之前的tree-lines)投影的损失最少.
首先节点$v\in l_0$，其权重为0，这是因为每个tree-line都有,
其次是节点$v \in p_1^f \cup \ldots \cup p_{k-1}^f$，权重为0，这是因为，即便我们再一次选中的$L$中有此节点，新的子空间也不会因为这个节点带来损失的减少(因为已经有了)
最后是其它的节点，可以想象，如果我们选中了这个节点，那么没有一棵树$t$, $v \in t$， 就会带来2点的距离减少，所以其权重设置为上面的形式.

算法自然是选择$p_L$中的节点权重和最大的.

一个例子:

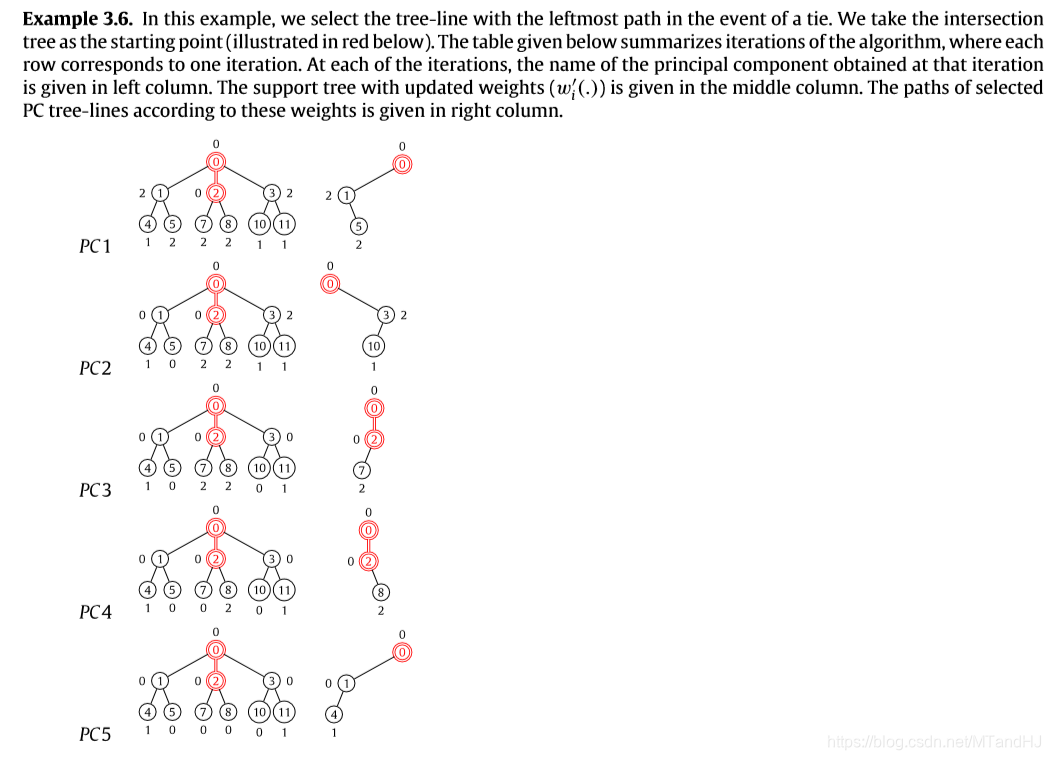
需要说明的是，这部分的证明我觉得是，就是正统的证明蛮有意思的.

后向的方法:

相应的算法:


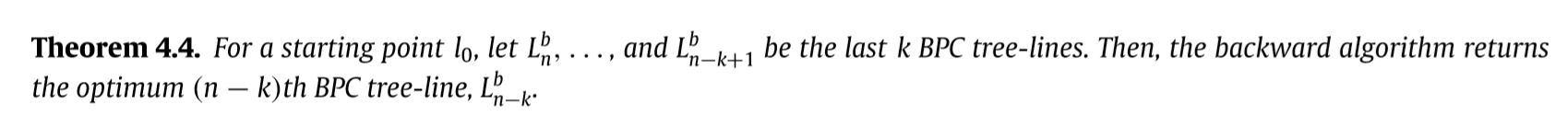
这么来理解权重的定义，首先，如果节点$v \in l_0$, 那么权重自然为0，因为每个$L$都有，所以不会剩下的子空间造成影响, 另外，如果v在超过俩条路径上存在，那么显然，我们去掉任意一条都不会导致这个节点消失于剩余的子空间，所以权重为0.
其它的情况，即有影响的情况，那么舍弃$v$会直接导致包含$v$的树与子空间的距离+2，所以才会有上面的定义.
例子:

还有一部分是为了说明，前向和后向的一致性，这部分的证明我没看.

其它

看其数值实验，很大程度上是利用投影的距离来进行一些分类啊之类的操作. 直观上，这么设计似乎能够抓住树形数据的主干，只是，我总感觉哪里怪怪的. 但是是蛮有趣的，在普通的PCA中，也会遇到类似类别的0, 1, 2的数据，这些数据，虽然硬用也是可以的，但是应该也是有更好的方法去针对. 眼前一亮，但怪怪的...