Proximal Algorithms
需要注意的一点是,本节所介绍的例子可以通过第二节的性质进行延展.
一般方法
一般情况下proximal需要解决下面的问题:
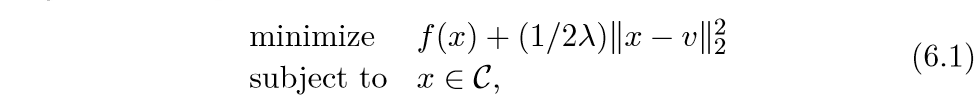
其中x∈Rn, C=domf.
我们可以使用梯度方法(或次梯度)方法来求解, 还有一些投影方法, 内点法等等.
二次函数
如果f(x)=(1/2)xTAx+bTx+c, 其中A∈Sn+,于是:
proxλf(v)=(I+λA)−1(v−λb)
证:
设φ(x)=(1/2)xTAx, 根据第二节介绍的仿射性质可得:
proxλf(v)=proxλφ(v−λb)
又∂φ=A, 故得证.
特别的f(x)=bTx+c则proxλf(v)=v−λb, f(x)=c, proxλf(v)=v, 而当f(x)=(1/2)∥⋅∥22时:
proxλf(v)=(11+λ)v
这玩意儿有时候被称为压缩算子.
估计proximal operator的时候,需要求解一个线性方程组:
(I+λA)x=v−λb
线性方程组怎么求解这里就不讨论了吧.
不过,这个应该多数用在f(x)+g(x)这种情况吧,因为如果单纯想要最小化f(x),直接可以求出显示解,所以可能是f(x)+|x|这种类型的?
平滑函数
文章里介绍了如何用梯度方法和牛顿方法,不提了.
标量函数
f:R→R∪{+∞}, 通过之前几节的介绍,这个情况还是蛮有意义的,因为通过proximal operator的可分性质等,有很好的扩展.
显然,此时,最优条件为:
v∈λ∂f(x)+x
比如:
f(x)=−logx⇒proxλf(v)=v+√v2+4λ2
又比如当f(x)=|x|:

一般的标量函数
如果对于f,其次梯度是可获得的,那么我们可以利用localization method来有效估计proxλf, 这种方法有点类似于二分法.
我们从[l,u]∈domf开始, 如果v在区间之外,返回最靠近v的点?(应该就是挑domf中最靠经v的点作为边界吧) 算法会在u−l<ϵ的时候终止.

注:上面的第一步的意思应该是如果v在区间里面就取v,否则取中间的点.
如果g>0,那么φ(z)≥φ(x)+g(z−x), 显然,当z>x不是最优的,而z=x−λg是一个下界. 为了说明这一点,假设hz∈∂f(z). 因为g>0,λ>0, 所以z<x,则hz≤h(因为凸函数的次梯度是单调的), 令:
gz=hz+(1/λ)(z−v)∈∂φ(z)
于是
hz+(1/λ)(z−v)=hz+(1/λ)(x−λ(h+(1/λ)(x−v))−v)
等式右边是hz−h≤0, 所以新的[l,u]就是一端小于0,一端大于0, 不过这对一开始的l,u有要求吧.
如果f是二阶连续可微的,那么,可以用guarded Newton方法来找x∗,不理解曲中的缘由,贴个图吧.

多边形
这一小节,考虑投影至多边形的问题,多边形可以用 一系列线性方程和不等式描述:
C={x∈Rn|Ax=b,Cx≤d}
其中A∈Rm×n,C=Rp×n.
投影问题可以表示为(计算prox便会遇到此问题):
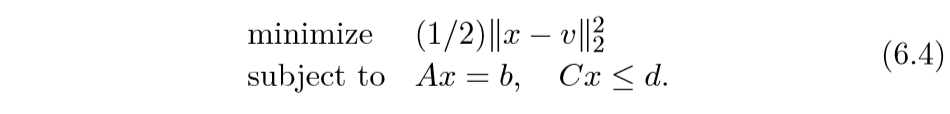
对偶
当m,p都远小于n的时候,利用对偶方法是方便的.
(6.4)的对偶问题是:
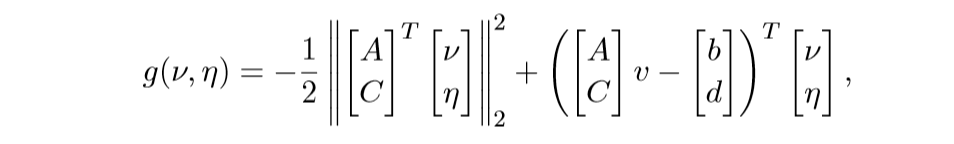
其中v∈Rm,η∈Rp为对偶变量(上面的式子不难推出,这里不证了).
对偶问题是:
maxg(v,η)s.t.η≥0
这是一个m+p个变量的二阶规划(QP)问题,且:
x∗=v−ATλ∗−CTv∗
这个最优解的恢复是由KKT条件得来的.上面的问题,似乎可以用内点法有效解决,下次找机会再看看. 文章还提到了如何使得QP问题能够简单并行,这里便不多赘述了.
仿射集合
即
C={x∈Rn|Ax=b}
则:
ΠC(v)=v−A†(Av−b)
其中A†是伪逆.
如果m<n,A满秩,那么:
ΠC(v)=v−AT(AAT)−1(Av−b)
这个我可以用一种比较麻烦的方法证明.
假设最优解为:v−AT(AAT)−1(Av−b)+u,因为
A(v−AT(AAT)−1(Av−b))=b
所以,根据线性方程组解的理论可知:
Au=0
那么问题可以转换为:
min∥AT(AAT)−1(Av−b)−u∥22s.t.Au=0
再根据线性方程组的理论可知,u属于A的核,设:
A=UDVT
其中U∈Rm×k,D∈Rk×k,V∈Rn×k.
我们只要找出AT(AAT)−1(Av−b)在核空间的投影即可:
(I−VVT)AT(AAT)−1(Av−b)=0
即投影为0,也就是说x=0, 这也就证明了
ΠC(v)=v−AT(AAT)−1(Av−b)
半平面
此时C={x|aTx≤b}, 而:
ΠC(v)=v−(aTv−b)+∥a∥22
其中(u)+=max{u,0}.
这个可以画个图来证明,注意到(aTv−b)+∥a∥22和点到直线距离的联系.
Box
box为如下形式C={x|l≤x≤u}, 及:
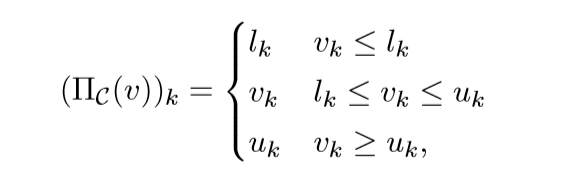
如果C=Rn+则:
ΠC(v)=v+
这个感觉是显然的.
Simplex
Simplex 为如下形式C={z|z≥0,1Tz=1}, 及
ΠC(v)=(v−ν1)+
对于某些ν∈R.
满足
1T(v−ν1)+=1
利用二分法可以求解.
Cones
令K为锥,以及K∗为其对偶锥. 那么问题为:
min∥x−v∥22s.t.x∈K
对偶锥的定义:
K∗={y|xTy≥0,∀x∈K}
对偶最优条件为:
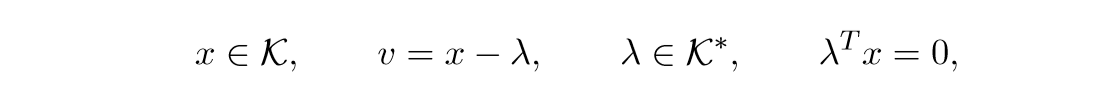
v=x−λ这个条件我是存疑的,这样子原问题应该是12∥x−v∥22,当然,这应该无伤大雅.
二阶锥
C={(x,t)∈Rn+1|∥x∥2≤t}

上面的东西,通过考虑下面的问题:
minx,t∥v−x∥22+(s−t)2s.t.∥x∥2≤t
可以获得, 第二种情况是不需讨论的, 那么先来看第一种情况。
在t≤∥v∥的情况下,x=tv∥v∥, 不妨令u=v∥v∥.则,原问题为:
min(∥v∥−t)2+(s−t)2
在t=∥v∥+s2处取得极值,但是∥v∥≤−s, 所以此时t≤0, 所以t=0. t>∥v∥的时候,x=v,于是原问题为:
min(s−t)2
那么t=∥v∥,显然没有0的时候小.
第三种情况的分析是类似的.
半正定锥
C=Sn+, 此时
ΠC(V)=n∑i=1(λi)+uiuTi
其中∑ni=1λiuiuTi为特征分解.
指数锥
不了解,截个图吧


Pointwise maximum and supremum
max
如果f(x)=maxixi, 根据其上镜图,我们有等价形式:
mint+(1/2λ)∥x−v∥22s.t.xi≤t,i=1,…,n
其拉格朗日对偶形式为:
L(x,t,μ)=t+(1/2λ)∥x−v∥22+μT(x−t1)
KKT条件为:

如果x∗i<t∗,则表示(通过第三个条件)μ∗i=0, 如果x∗=t∗,则表示u∗i=(1/λ)(vi−t∗), 又μ∗i≥0, 总结为:
μ∗i=(1/λ)(vi−t∗)+
再根据第五个条件可得:
n∑i=1(1/λ)(vi−t∗)+=1
这个可以用半分法求解,初始的区间为[minivi−(1/n),maxivi].
最后
x∗=min{t∗,vi}.
support function
C是一个凸集,其support function为:
SC(x)=supy∈CyTx.
support function的共轭是指示函数.
S∗C(z)=supx(zTx−f(x))=IC.
通过Moreau 分解我们知道:
proxλSC(v)=v−λΠC(v/λ)
一个例子是f(x)=x[1]+x[2]+…+x[k], 表x的前k个最大的和,可以用以下凸集的support function来表示:
C={y|0⪯y⪯1,1Ty=k}.
Norms and norm balls
f=∥⋅∥为一般的定义在Rn上的范数,则f∗=IB, 其中B为对偶范数的单位球.
我们知道f(x)=supy{yTx|∥y∥∗≤1}, 此为B={y|∥y∥∗≤1}的支撑函数,故f∗=IB.
对偶不是共轭的特例?
于是根据Moreau分解,有以下式子成立:
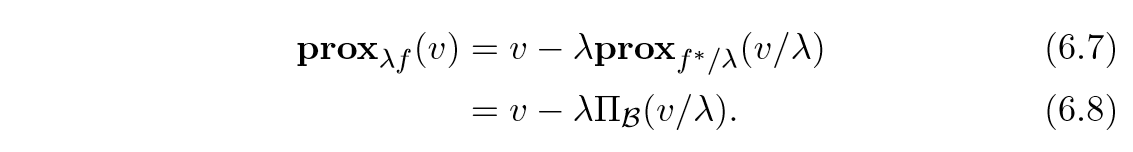
Euclidean 范数
当f=∥⋅∥2的时候:
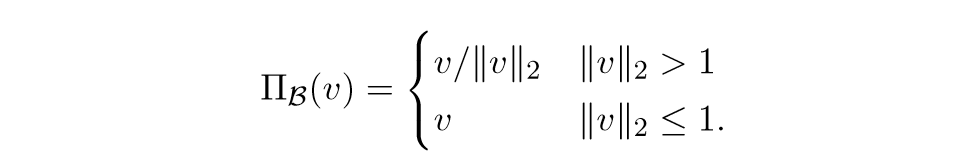
以及:
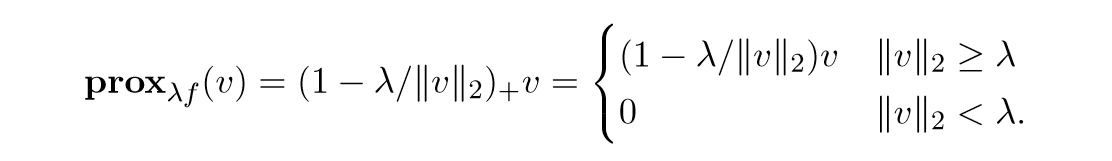
ℓ1 and ℓ∞ norms
ℓ∞的B是box,所以根据之前讨论过的:

引文ℓ1和ℓ∞互为对偶,所以当f=∥⋅∥1的时候:

可以用更为紧凑的形式表示:
proxλf(v)=(v−λ)+−(−v−λ)+.
欲计算ℓ∞的proximal operator并不容易,因为投影到ℓ1的单位球比较麻烦.
我们需要计算一个λ,满足:
n∑i=1(|vi|−λ)+=1.
可以用类似半分法的方法求解.
Elastic net
f(x)=∥x∥1+(γ/2)∥x∥22, γ>0.
此时
proxλf(v)=(11+λγ)proxλ∥⋅∥1(v).
范数和
f(x)=∑g∈G∥xg∥2
其中G是[n]的一个分割, 则:
(proxλf(v))g=(1−λ∥vg∥2)+vg
sublevel set and epigradph
下水平集
f的t−下水平集合为:
S={x∈Rn|f(x)≤t}
假设v∉S , 否则ΠS(v)=v.
此时ΠS(v)可以转化为下列问题:
min12∥x−v∥22s.t.f(x)≤t.
通过KKT条件可得最优条件为:
0∈x−v+λ∂f(x),f(x)=t,λ>0
第一个条件,表示ΠS(v)=proxλf(v), 再根据第二个条件可得:
f(proxλf(v))=t
我们可以通过二分法来寻找λ.
上镜图
函数f的上镜图为:
epif={(x,t)|x∈domf,f(x)≤t}.
针对Πepif(v,s):
min12∥x−v∥22+12(t−s)2s.t.f(x)≤t.
同样假设f(v)>sKKT条件为:
f(x)=t0∈x−v+λ∂f(x)t−s=λλ>0.
所以
v∈x+(f(x)−s)∂f(x).
论文说这个问题比较难成立,有另外一种表示方法:

不知道怎么推的.
Matrix functions
Elementwise functions
这里将矩阵A∈Rm×n视为Rmn的向量,就能利用之前的方法了,比如ℓ1的方法:
∥A∥1=m∑i=1n∑j=1|aij|
正交不变
函数F:Rm×n→R,正交不变是指:
F(VXU)=F(X).
其中U∈Rn×n,V∈Rm×m为正交矩阵, 这也意味着:
F(x)=F(diag(σs(X))).
其中σs:Rm×n→Rmin{m,n}是奇异值映射.
正交不变算子F可以表示为:f∘σs, 而
∂F(X)={Vdiag(μ)U|μ∈∂f(σs(X)},
其中X=Vdiag(σs(X))U. 这个的推导见之前关于矩阵次梯度的介绍.
这意味着:
proxλF(A)=Vdiag(proxλf(σs(A)))U.
这个没依照论文来,论文似乎有更加直接的证明方法,我来讲一下我的:
proxλF(A)=argminλF(X)+12∥X−A∥2F
最优条件为:
λ∂F(X)+X=A.
假设X=Vdiag(σs(X))U, 则:
V(λdiag(μ)+diag(σs(X))U=A.
显然A的奇异值分解也为:
A=Vdiag(σs(A))U⇒λdiag(μ)+diag(σs(X))=diag(σs(A))
而
proxλf(σs(A))=argminσs(X)λf(σs(X))+12∥σs(X)−σs(A)∥22.
其最优条件为:
λu+σs(X)−σs(A)=0.
显然二者的最有条件是一样的,所以成立.
当F:Sn→R, 且F(UXUT)=F(X):
proxλF(A)=Udiag(proxλf(σ(A)))UT
其中A=Udiag(σ(A))UT.
后面还有一些关于矩阵范数,一些特殊集合的投影,以及如何求解对数障碍问题.

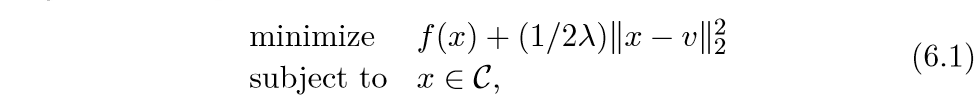



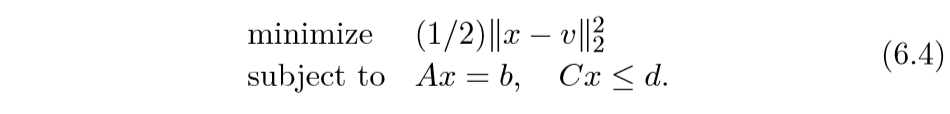
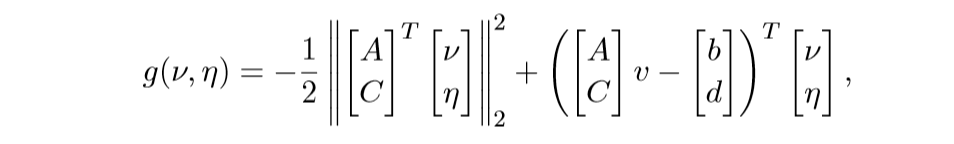
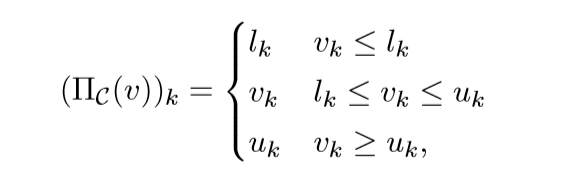
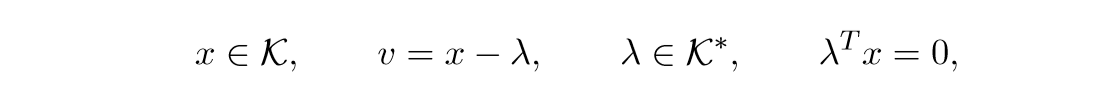




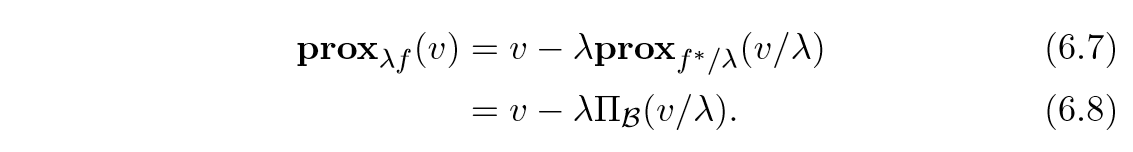
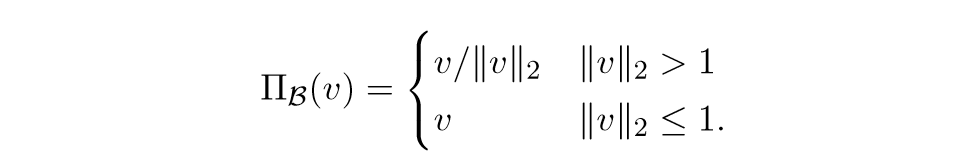
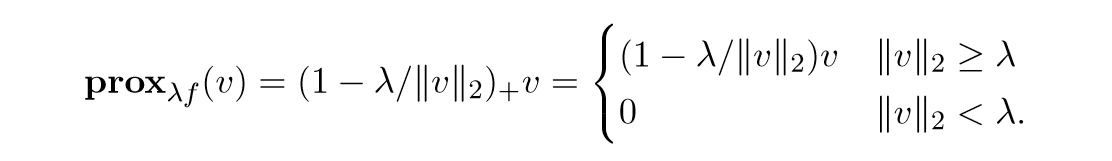








【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 【自荐】一款简洁、开源的在线白板工具 Drawnix