一些矩阵范数的subgradients

引
正交不变范数
算子范数

《Subgradients》
Subderivate-wiki
Subgradient method-wiki
《Subgradient method》
Subgradient-Prof.S.Boyd,EE364b,StanfordUniversity
《Characterization of the Subdifferential of Some Matrix Norms 》

这篇文章主要参考：

《Characterization of the Subdifferential of Some Matrix Norms 》

引

矩阵 $A \in \mathbb{R}^{m\times n}$ ， $\|\cdot\|$ 为矩阵范数，注意这里我们并没有限定为何种范数。那么 $\|A\|$ 的次梯度可以用下式表示：

\partial ‖ A ‖ = {G \in R^{m \times n} | ‖ B ‖ > ‖ A ‖ + t r a c e [(B - A)^{T} G], a l l B \in R^{m \times n}}

$\partial \|A\| = \{G \in \mathbb{R}^{m\times n}|\|B\| > \|A\| +\mathrm{trace}[(B-A)^TG],all \: B \in \mathbb{R}^{m \times n} \}$

这个定义和之前提到的定义是相一致的，事实上， $\mathrm{trace}(A^TB)$ 就相当于将 $A$ 和 $B$ 拉成俩个长向量作内积，比较实质就是对应元素相乘再相加。

$G \in \partial \|A\|$ 等价于：
在这里插入图片描述
在我看的书里面，对偶范数一般用 $\|\cdot\|_*$ 表示，且是如此定义的：

‖ z ‖_{*} = sup {z^{T} x | ‖ x ‖ \leq 1}

$\|z\|_* = \sup \{z^Tx| \|x\| \le 1\}$

因为下面还有很多地方是采取截图的形式展示的，所以还是沿袭论文的符号比较好，这里只是简单提一下。
至于为什么等价，论文里面没有提，我只能证明，满足那俩点条件的 $G$ 是 $\|A\|$ 的次梯度，而不能证明所有次梯度都满足那俩个条件。
证明如下：
假设 $G$ 满足上面的条件，那么：

t r a c e [(B - A)^{T} G] = - ‖ A ‖ + t r a c e (B^{T} G) \Rightarrow ‖ A ‖ + t r a c e [(B - A)^{T} G] = t r a c e (B^{T} G)

$\mathrm{trace}[(B-A)^TG]=-\|A\|+\mathrm{trace}(B^TG) \\ \Rightarrow \|A\| + \mathrm{trace}[(B-A)^TG] = \mathrm{trace}(B^TG)$

又

t r a c e (\frac{B^{T}}{‖ B ‖} G) \leq 1 = \frac{‖ B ‖}{‖ B ‖}

$\mathrm{trace}(\frac{B^T}{\|B\|}G) \le 1=\frac{\|B\|}{\|B\|}$

所以

‖ B ‖ \geq ‖ A ‖ + t r a c e [(B - A)^{T} G]

$\|B\|\ge \|A\| + \mathrm{trace}[(B-A)^TG]$

所以 $G \in \partial \|A\|$ '
不好意思，我想到怎么证明啦！下证， $G \in \partial \|A\|$ 必定满足上述的条件，我们先说明范数的一些性质：
齐次： $\|tA\|=|t|\|A\|$
三角不等式： $\|A+B\| \le \|A\|+\|B\|$
既然对所有 $B \in \mathbb{R}^{m \times n}$ 成立：

‖ B ‖ \geq ‖ A ‖ + t r a c e [(B - A)^{T} G]

$\|B\| \ge \|A\| + \mathrm{trace}[(B-A)^TG]$

令 $B=1/2A$ ,可得：

t r a c e (A^{T} G) \geq ‖ A ‖

$\mathrm{trace}(A^TG) \ge \|A\|$

又

‖ A + B ‖ \leq ‖ A ‖ + ‖ B ‖ \leq ‖ A + B ‖ - t r a c e [B^{T} G] + ‖ B ‖ \Rightarrow t r a c e (B^{T} G) \leq ‖ B ‖

$\|A+B\| \le \|A\| + \|B\| \le \|A+B\|-\mathrm{trace}[B^TG]+\|B\| \\ \Rightarrow \mathrm{trace}(B^TG)\le \|B\|$

所以:

‖ A ‖ \leq t r a c e (A^{T} G) \leq ‖ A ‖ \Rightarrow t r a c e (A^{T} G) = ‖ A ‖

$\|A\| \le \mathrm{trace}(A^TG) \le \|A\| \Rightarrow \mathrm{trace}(A^TG)=\|A\|$

到此第一个条件得证。
又：

t r a c e (B^{T} G) \leq ‖ B ‖ \Rightarrow t r a c e (\frac{B^{T}}{‖ B ‖} G) = ‖ G ‖^{*} \leq 1

$\mathrm{trace}(B^TG)\le \|B\| \Rightarrow \mathrm{trace}(\frac{B^T}{\|B\|}G) = \|G\|^*\le 1$

第二个条件也得证。漂亮！

正交不变范数

正交不变范数定义如下：

‖ U A V ‖ = ‖ A ‖

$\|UAV\| = \|A\|$

其中 $U,V$ 为任意正交矩阵（原文是 $\|UVA\|=\|A\|$ ，我认为是作者的笔误）。
注意，如果范数 $\|\cdot\|$ 是正交不变的，那么其对偶范数同样是正交不变的，证明如下：
既然：

‖ Z ‖^{*} = sup {t r a c e (Z^{T} X) | ‖ X ‖ \leq 1}

$\|Z\|^*=\sup \{\mathrm{trace}(Z^TX)|\|X\|\le1 \}$

‖ U Z V ‖^{*} = sup {t r a c e (V^{T} Z^{T} U^{T} X) | ‖ X ‖ \leq 1}

$\|UZV\|^*=\sup \{\mathrm{trace}(V^TZ^TU^TX)|\|X\|\le1 \}$

令 $UXV$ 替代 $X$ 代入即可得：

\begin{array}{ll} ‖ U Z V ‖^{*} & = sup {t r a c e (V^{T} Z^{T} U^{T} X) | ‖ X ‖ \leq 1} \\ = sup {t r a c e (V^{T} Z^{T} U^{T} U X V) | ‖ U X V ‖ \leq 1} \\ = sup {t r a c e (Z^{T} X) | ‖ X ‖ \leq 1} \\ = ‖ Z ‖^{*} \end{array}

$\begin{array}{ll} \|UZV\|^*&=\sup \{\mathrm{trace}(V^TZ^TU^TX)|\|X\|\le1 \}\\ &=\sup \{\mathrm{trace}(V^TZ^TU^TUXV)|\|UXV\|\le1 \}\\ &= \sup \{\mathrm{trace}(Z^TX)|\|X\|\le1 \}\\ &= \|Z\|^* \end{array}$

最后第二个等式成立根据迹的性质和 $\|\cdot\|$ 的题设。

我们假设矩阵 $A$ 的SVD分解为:

A = U Σ V^{T}

$A = U\Sigma V^T$

其中 $\Sigma \in \mathbb{R}^{m \times n}$ 为对角矩阵（那种歪歪的对角矩阵）， $U$ 和 $V$ 的列我们用 $u_i,v_i$ 来表示。
假设其奇异值：

σ_{1} \leq σ_{2} \leq \dots \leq σ_{n}

$\sigma_1\le \sigma_2 \le \ldots \le \sigma_n$

降序排列。
所有这样的（正交不变？）范数都能用下式来定义：

‖ A ‖ = ϕ (σ)

$\|A\| = \phi(\sigma)$

其中 $\sigma = (\sigma_1, \ldots, \sigma_n)^T$ , $\phi$ 是一个对称规范函数(symmetirc gague function)，满足:
在这里插入图片描述
上面这个东西我也证明不了，不过至少谱范数和核函数的确是这样的。

$\phi$ 的对偶可以用下式来表示：

ϕ^{*} = max_{ϕ (y) = 1} x^{T} y

$\phi^*= \max \limits_{\phi(y)=1} x^Ty$

而且其次梯度更矩阵范数又有相似的一个性质：
在这里插入图片描述
证明是类似的，不多赘述。

一种常见的正交不变范数可由下式定义：

‖ A ‖ = ‖ σ ‖_{p}

$\|A\| = \|\sigma\|_p$

比较经典的， $p=1$ 对应核范数， $p=2$ 对应F范数， $p=\infty$ 对应谱范数。

定理1

在这里插入图片描述

证明如下：

这一部分的证明需要注意，不要把 $A$ 当成题目中的 $A$ ，当成 $A+rR$ 可能更容易理解。
在这里插入图片描述

这部分的证明，主要是得出了 $\sigma_i(\gamma)$ 的一个泰勒展开，要想证明这个式子成立，可以利用上面的公式，也可以这么想。 $\sigma_i(\gamma)$ 是 $A+\gamma R$ 的第 $i$ 个奇异值：

lim_{γ \to 0^{+}} \frac{σ_{i} (γ) - σ_{i}}{γ} = lim_{γ \to 0^{+}} \frac{σ_{i} (A + γ R) - σ_{i}}{γ} = lim_{γ \to 0^{+}} \frac{u_{i} (γ)^{T} (A + γ R) v_{i} (γ) - σ_{i}}{γ}

$\lim_{\gamma \rightarrow 0^+} \frac{\sigma_i(\gamma)-\sigma_i}{\gamma}=\lim_{\gamma \rightarrow 0^+} \frac{\sigma_i(A+\gamma R)-\sigma_i}{\gamma}=\lim_{\gamma \rightarrow 0^+} \frac{u_i(\gamma)^T(A+\gamma R)v_i(\gamma)-\sigma_i}{\gamma}$

即为：

lim_{γ \to 0^{+}} \frac{u_{i} (γ)^{T} A v_{i} (γ) - σ_{i}}{γ} + u_{i}^{T} R v_{i}

$\lim_{\gamma \rightarrow 0^+} \frac{u_i(\gamma)^TAv_i(\gamma)-\sigma_i}{\gamma}+u_i^TRv_i$

所以左边这项等于0？
在这里插入图片描述

下面的证明中，第一个不等式成立的原因是：

ϕ (σ) \geq ϕ (σ (γ)) + (σ - σ (γ))^{T} d (γ)

$\phi(\sigma) \ge \phi(\sigma(\gamma))+(\sigma-\sigma(\gamma))^T\mathrm{d}(\gamma)$

又 $\sigma(\gamma)^T\mathrm{d}(r)=\phi(\sigma(r))$
在这里插入图片描述

类似地，我们就可以得到下面的分析：
在这里插入图片描述
有一点点小问题是，没有体现出 $\max$ 的，不过从(2.5)看，因为这个不等式是对所有 $\mathrm{d}\in \partial \phi(\sigma)$ 都成立的，所以结果成立。怎么说呢，这个有点像是上确界的东西。

我们定义符号 $\mathrm{conv} \{\cdot \}$ ，表示集合的凸包。

定理2

注意，我们的最终目的是找到 $\partial \|A\|$ 利用前面的铺垫我们可以得到定理2：

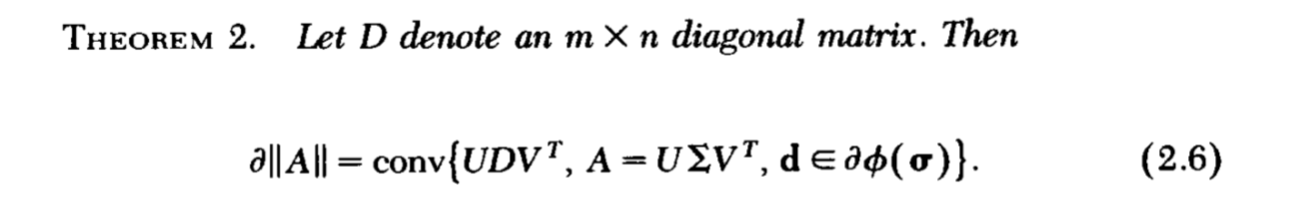
在这里插入图片描述
相当有趣的一个东西。

下面是证明：

证明总的是分俩大部分来证明的，首先得证明 $G \in \mathrm{conv} \{S(A)\}$ 满足上面的俩个条件，即是次梯度，再证明，不存在一个次梯度不属于 $\mathrm{conv} \{S(A)\}$ 。
其实下面这部分的证明，我觉得用 $A = U_i\Sigma_i V_i^T$ 表示比较好，作者的意思应该是奇异值分解可以用不同的序，毕竟我们不能要求凸包中的元素有合适的序。
在这里插入图片描述

下面这部分的证明，感觉没什么好讲的。
在这里插入图片描述
下面这部分证明，打问号的地方我有疑惑，以为我觉得只能知道 $\phi^*(\mathrm{d}_i)\le 1$ ，而且在这个条件下，证明依旧。好吧，我明白了，因为： $\phi^*(\mathrm{d}_i)=\max \limits_{\phi(x)=1}\mathrm{d}_i^Tx$ ，又 $\mathrm{d}_i \in \phi(\sigma)$ ,所以只需令 $x=\sigma/|\phi(\sigma)$ 即可得 $\phi^*(\mathrm{d}_i)=1$ 。
在这里插入图片描述
到此，俩个条件满足，第一部分证毕。

第二部分用到了一个理论，我没有去查阅。这部分证明的思想是，即便存在这么一个 $G$ 不属于 $\mathrm{conv}S(A)$ ， $G$ 依旧得满足 $\mathrm{trace}(R^TG) \le \max \limits_{\mathrm{d \in \partial \phi(\sigma)}} \sum \limits_{t=1}^n d_i u_i^TRv_i$ （要知道，后面这个部分是类似右导数的存在！！！），这个的原理是一种极限的思想，不好表述，但是真的真的蛮容易证明的。
在这里插入图片描述

例子：谱范数

在这里插入图片描述

凸包，凸包，切记切记。

例子：核范数

在这里插入图片描述
上面倒数第二行那个式子成立，要注意 $\sum_i \lambda_i =1$ 这个条件。

注意：这里出现 $Y,Z$ 的原因是 $U^{(2)},V^{(2)}$ 对应的奇异值为0，所以其顺序是任意的，并没有对应一说。

算子范数

让 $\|\cdot\|_A$ 和 $\|\cdot\|_B$ 分别表示定义在 $\mathbb{R}^m$ 和 $\mathbb{R}^n$ 上的范数，那么对于矩阵 $A \in \mathbb{R}^{m \times n}$ 上的算子范数，可以如下定义：

‖ A ‖ = max_{‖ x ‖_{B} = 1} ‖ A x ‖_{A}

$\|A\| = \max \limits_{\|x\|_B=1} \|Ax\|_A$

注意，矩阵范数，向量范数都满足引里的那个等价条件（实际上，只需满足正定性和三角不等式即可，就能推出那个等价条件）。

定义 $\Phi(A)$ :
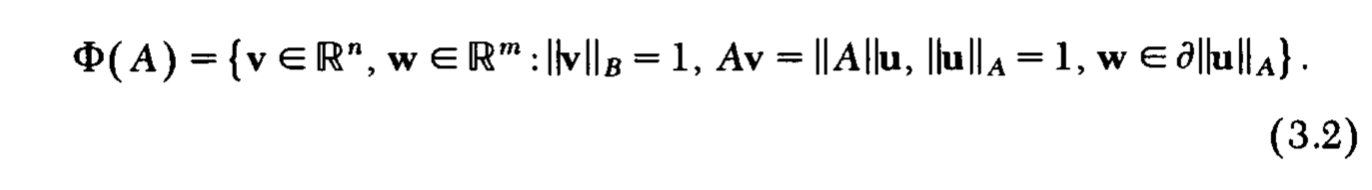
在这里插入图片描述

定理3

类似的，我们有定理3：
在这里插入图片描述

这部分的推导是类似的：
在这里插入图片描述

下面这部分和之前的是不同的，这么大费周章，就是为了证明最后收敛的结果在 $\Phi(A)$ 中，之间没有这部分的证明，是因为凸函数次梯度的集合是闭凸的？
在这里插入图片描述

定理4

这个定理，就是为了导出 $\|A\|$ 的次梯度。

在这里插入图片描述
这部分首先利用迹的性质，再利用 $Av_i=\|A\|u_i$

$w_i^TRv_i \le \|R\|$ 的原因是 $\|w_i\|_A^* \le1$ ,
又 $\frac{\|Rv_i\|_A}{\|R\|}=\frac{\|Rv_i\|_A}{\max \limits_{\|v\|\_B=1} \|Rv\|_A}\le1$ (至少 $\|Rv_i\|_A=1$ )，所以有上面的结果。

到此，我们证明了， $S(A)$ 中的元素均为次梯度，下证凡是次梯度，必属于 $S(A)$ 。

这部分证明没有需要特别说明的。
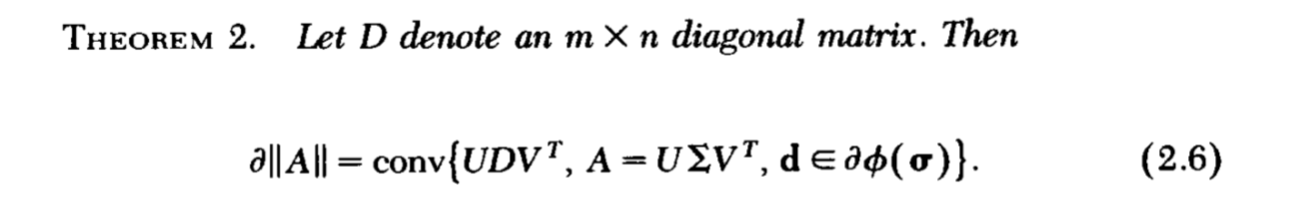
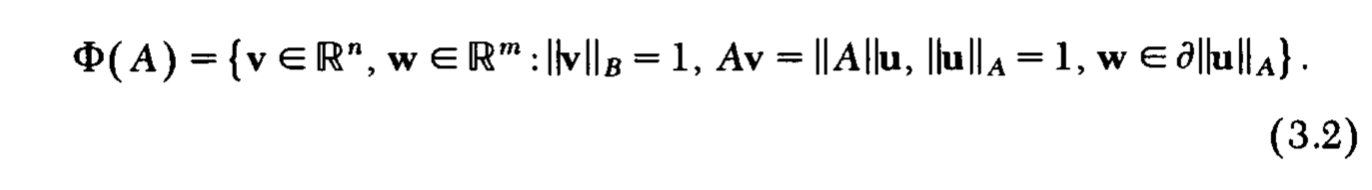
在这里插入图片描述

例子 $\ell_2$

在这里插入图片描述

posted @ 2019-04-12 16:07 馒头and花卷阅读(2970) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

馒头and花卷

一些矩阵范数的subgradients

引

正交不变范数

定理1