FAST MONTE CARLO ALGORITHMS FOR MATRICES II (快速的矩阵分解策略)
Drineas P, Kannan R, Mahoney M W, et al. Fast Monte Carlo Algorithms for Matrices II: Computing a Low-Rank Approximation to a Matrix[J]. SIAM Journal on Computing, 2006, 36(1): 158-183.
问题
我们有一个矩阵\(A \in \mathbb{R}^{m \times n}\),我们需要对其进行矩阵的分解,很完美很经典的一种方法就是SVD,但是这种方法 的缺憾在于,需要的计算量比较大。不妨设\(A\)的奇异值分解为:
其中:\(U = [u^1, u^2, \ldots, u^m] \in \mathbb{R}^{m \times m}\),\(V = [v^1, v^2, \ldots, v^n] \in \mathbb{R}^{n \times n}\), \(\Sigma = diag(\sigma_1, \sigma_2, \ldots, \sigma_{\rho} \in \mathbb{R}^{m \times n}), \rho=\min{m, n}\)。
假设\(\sigma_1 \ge \sigma_2 \ge \sigma_3 \ldots \ge \sigma_r > \sigma_{r+1}=\ldots=\sigma_{\rho}=0\),那么\(rank(A) = r\),矩阵\(A\)的零空间\(\mathrm{null}(A)=span(v^{r+1}, \ldots, v^{\rho})\),矩阵\(A\)的值域为\(\mathrm{range}(A) = span(u^1, \ldots, u^r)\)
那么\(A\)可以有下面的方法表示:
到这里,我们简单介绍了SVD。回到正题,为了避免计算量大的问题,这篇文章提出了一种基于蒙特卡洛采样的矩阵分解的算法。
算法
为什么可以这么采样,以及概率的选择,在FAST MONTE CARLO ALGORITHMS FOR MATRICES I中有介绍。算法的思想很朴素,但是通篇的证明让人抓耳挠腮。
LINEARTIMESVD 算法

CONSTANTTIMESVD 算法

理论
俩个算法,作者都给除了形如下的界(大概率):
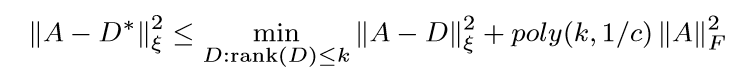
\(\xi=2,F\),\(D*\)是\(A\)的一个低秩的逼近。
算法1的理论
作者先给出的是下面的证明,
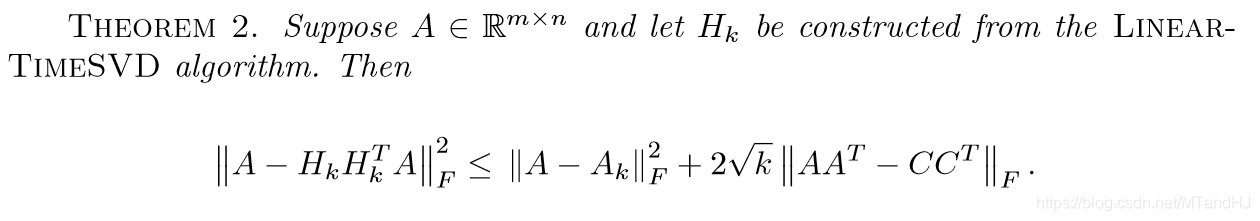
我们先来分析上面的不等式,比较可以发现\(D^* = H_kH_K^TA\),注意,\(C = H\Sigma_CY\),\(A_k = U_kU_k^TA\)
我们先来看第一部分的证明,这部分只是简单地利用了\(Tr\)的性质。

第二部分的证明,是为了导出定理2的后面部分,第一个不等式,利用了Cauchy-Schwarz不等式,把\(|\|A^TH_k\|_F^2- \sum_{t=1}^k \sigma_t^2 (C)|\)看成\(|\sum \limits_{t=1}^k (|A^Th^t|^2-\sigma_t^2(C))\times 1|\)这就成了俩个向量的内积了。第二个等式易证,第三个等式同样。最后一个不等式,是因为,如果我们将\(h^t, t=1,\ldots,k\)扩充为一组标准正交基\(h^t,t=1,\ldots,m\),那么\(\sum \limits_{t=1}^{m}({h^t}^T(AA^T-CC^T)h^t)=\sum \limits_{t=1}^{m} \lambda_t\),其中\(\lambda_t\)是\(AA^T-CC^T\)的特征值(降序排列)。我们知道\(a+b=c, a,b>0\),\(max(a^2+b^2)=c^2\),通过数学归纳法,容易得到最后一个不等式。
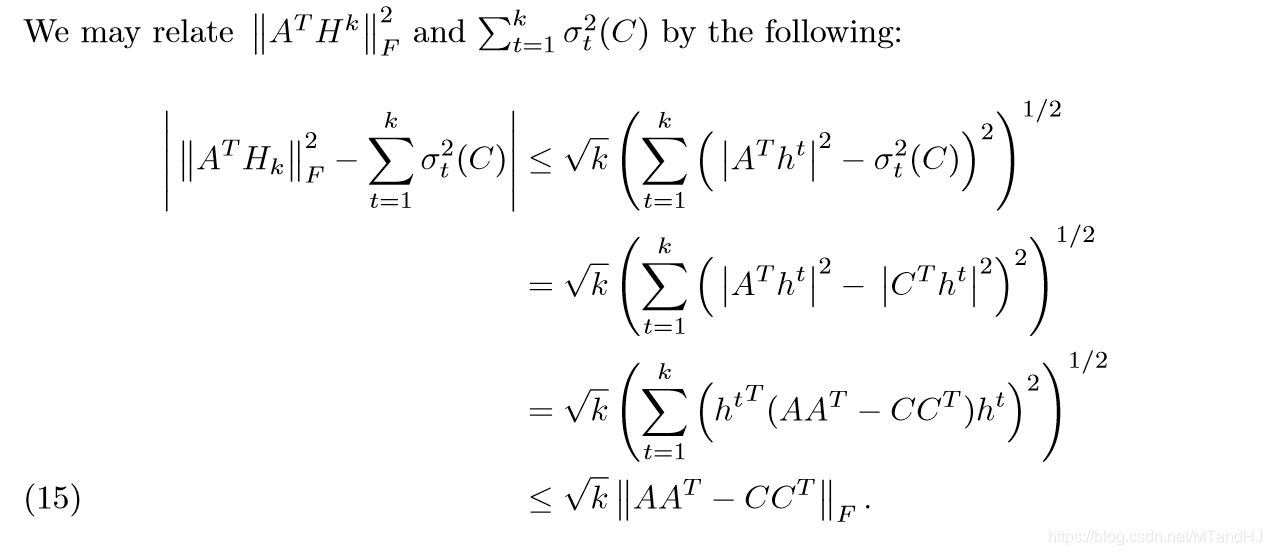
第三部分的证明,第一个不等式,同样利用了Cauchy-Schwarz不等式,接下来的等式和不等式易证。最后一个不等式,利用了Hoffman-Wielandt不等式:
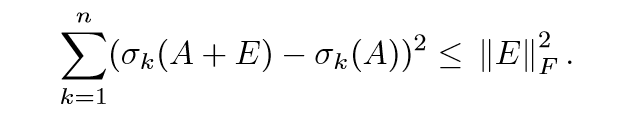
这个不等式的证明比较麻烦,在《代数特征值问题》一书中有提(虽然书中矩阵是方阵,可以类似地推导)。
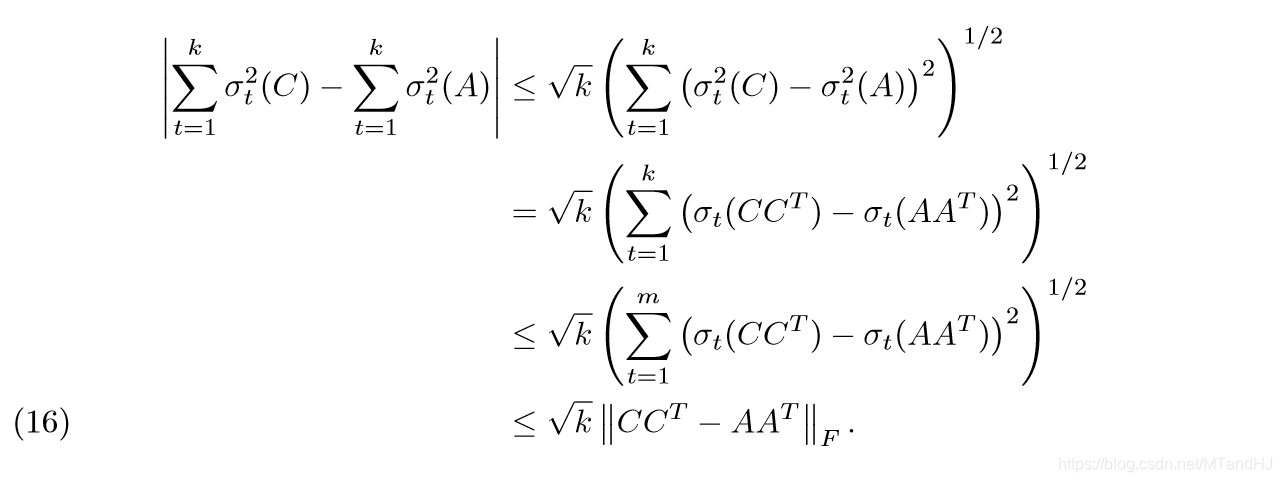
最后一部分通过加一项减一项就可以得到了。

到此关于\(F\)范数的一个理论就得到了,接下来作者给出了关于\(2\)范数的性质。
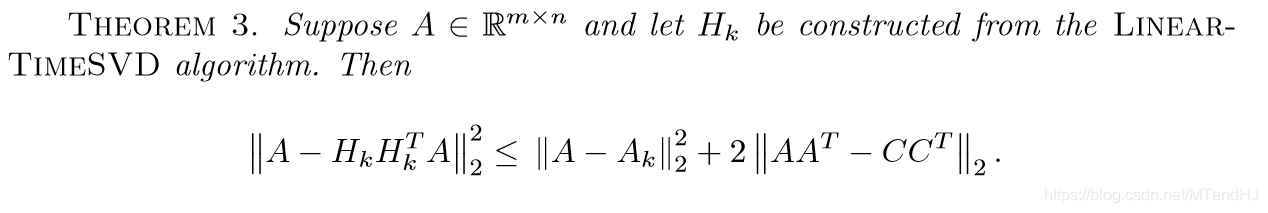
通过与定理2的比较可以发现,缺了\(\sqrt{k}\)这一部分。
令\(\mathcal{H}_k=range(H_k) = span(h^1,\ldots,h^k)\),\(\mathcal{H}_{m-k}\)为其正交补。那么,对于任意向量\(x \ in \mathbb{R}^m\),可以分解为\(x = \alpha y + \beta z,y\in \mathcal{H}_k, z \in \mathcal{H}_{m-k}\),而且\(\alpha^2 + \beta^2 = 1\)
第一部分的证明,不等式部分利用了三角不等式,及\(\alpha, \beta \le 1\)的性质。最后一个等式成立的原因是\(H_kH_k^T y = y, y \in \mathcal{H}_k\)
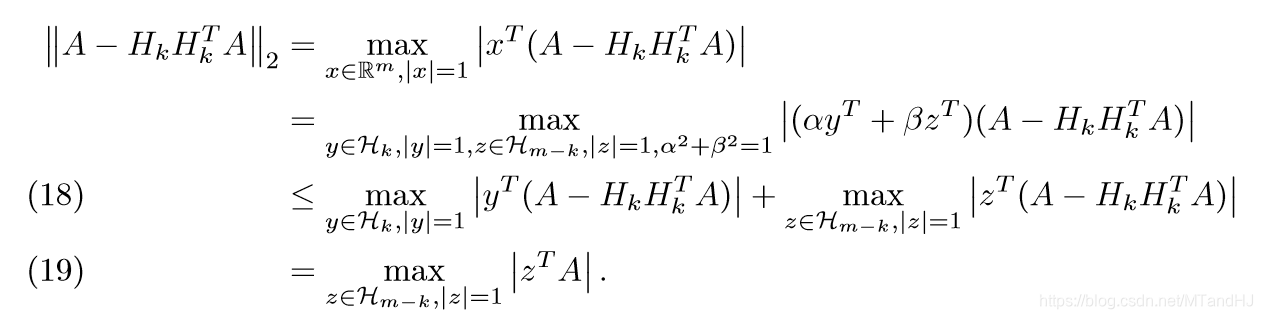
第二部分的证明,第一个不等式部分的后半部分是显然的,前半部分是因为\(z \in \mathcal{H}_{m-k}\),第二个不等式,我们需要利用下面的一个性质:
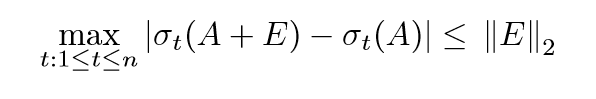
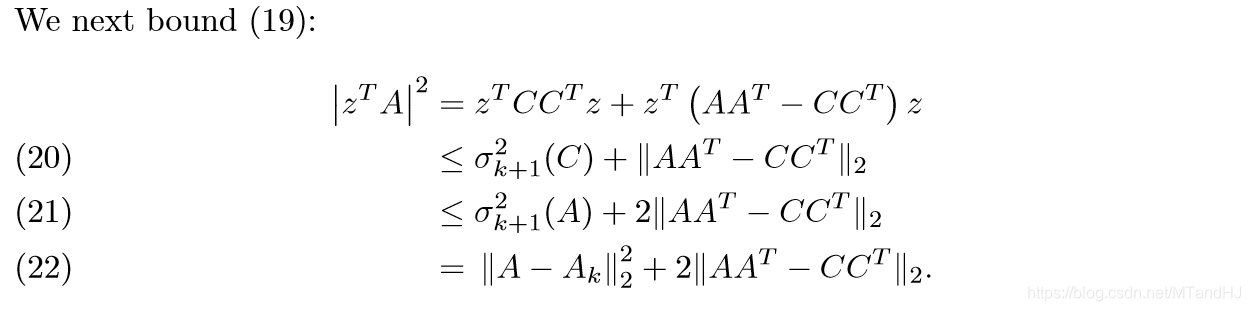
到此,这部分的定理也证毕了。
接下来,还有定理4:

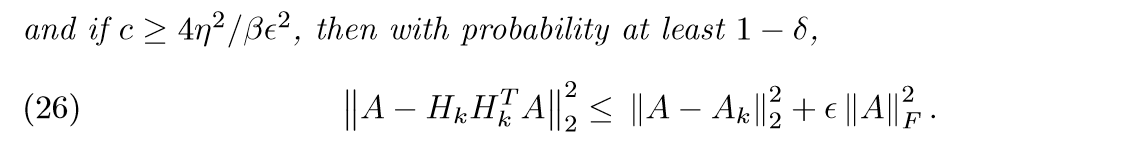
这部分的证明,需要利用FAST MONTE CARLO ALGORITHMS FOR MATRICES I 中的性质,这里便不讲了。
算法2 的理论
我们只给出了结果,证明实在有些长。

代码
import numpy as np
class FastSVD:
def __init__(self, A):
self.m, self.n = A.shape
self.A = np.array(A, dtype=float)
self.norm_F = FastSVD.forbenius(self.A)
@classmethod
def forbenius(cls, A):
"""矩阵A的F范数"""
return np.sum(A ** 2)
@classmethod
def approx_h(cls, A):
"""A=UDV^T, 我们要U"""
value, vector = np.linalg.eig(A.T @ A)
U = []
for i in range(len(value)):
if value[i] < 1e-15:
break
else:
U.append(A @ vector[:, i] / np.sqrt(value[i]))
return np.array(U).T
def fastSVD(self, c):
"""返回的H的每一列是我们所需要的"""
assert isinstance(c, int), "{0} is not an integer"
p = np.array([self.A[:, i] @ self.A[:, i] / self.norm_F for i in range(self.n)])
lucky_dog = np.random.choice(np.arange(self.n), size=c, replace=True, p=p)
C = np.zeros((self.m, c))
for t, dog in enumerate(lucky_dog):
C[:, t] = self.A[:, dog] / np.sqrt(c * p[dog])
H = FastSVD.approx_h(C)
return H


