最速下降方法和Newton方法
最速下降方法
\(f(x+v)\)在\(v=0\)处的一阶泰勒展开为：
\(\nabla f(x)^{T}v\)是\(f\)在\(x\)处沿\(v\)的方向导数。它近似给出了\(f\)沿小的步径\(v\)会发生的变化。
在\(v\)的大小固定的前提下，讨论如何选择\(v\)使得方向导数最小是有意义的，即：
最速下降方向就是一个使\(f\)的线性近似下降最多的具有单位范数的步径。注意，这里的单位范数，并不局限于Euclid范数。
我们先给出最速下降方法的算法，再介绍几种范数约束。
Euclid范数和二次范数
Euclid范数
显然，这时的方向就是负梯度方向。
二次范数
我们考虑二次范数
其中P为n阶对称正定矩阵。
这时的最优解为：
这个最优解，可以通过引入拉格朗日乘子，求解对偶函数KKT条件获得，并不难，就不写了。
基于坐标变换的解释
二次范数，可以从坐标变换的角度给出一个解释。
我们定义线性变换：
那么：
\(g\)在\(\bar{x}\)出的负梯度方向为：
注意，并没有归一化。
又，我们已经知道\(\Delta x = -P^{-1} \nabla f(x)\)(只是方向而已)，所以：
同样的线性变换。换言之，二次范数\(\|\cdot\|_P\)下的最速下降方向可以理解为对原问题进行坐标变换\(\bar{x}=P^{1/2}x\)后的梯度方向。辅以下图便于理解。
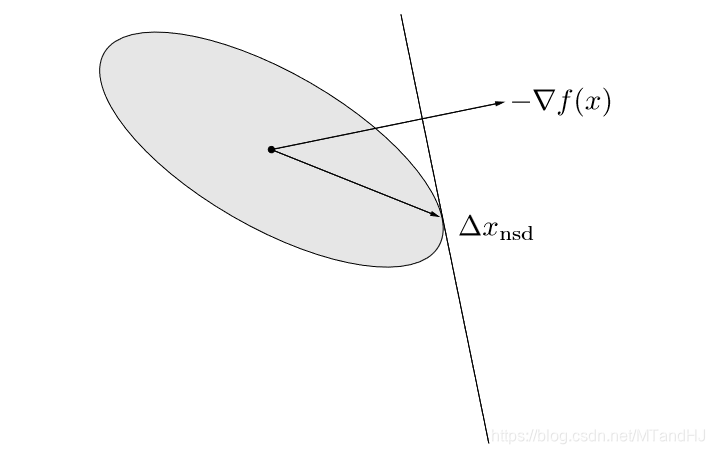
采用\(\ell_1\)-范数的最速下降方向
这个问题的刻画如下：
\(\ell_1\)即各分量绝对值之和，所以，只需把\(\nabla f(x)\)绝对值分量最大的那个部分找出来即可。不妨设，第\(i\)个分量就是我们要找的，那么：
其中，\(e_i\)表示第\(i\)个基向量。
所以，在每次下降过程中，都只是改变一个分量，所以\(\ell_1\)-范数的下降，也称为坐标下降算法。
辅以下图以便理解：
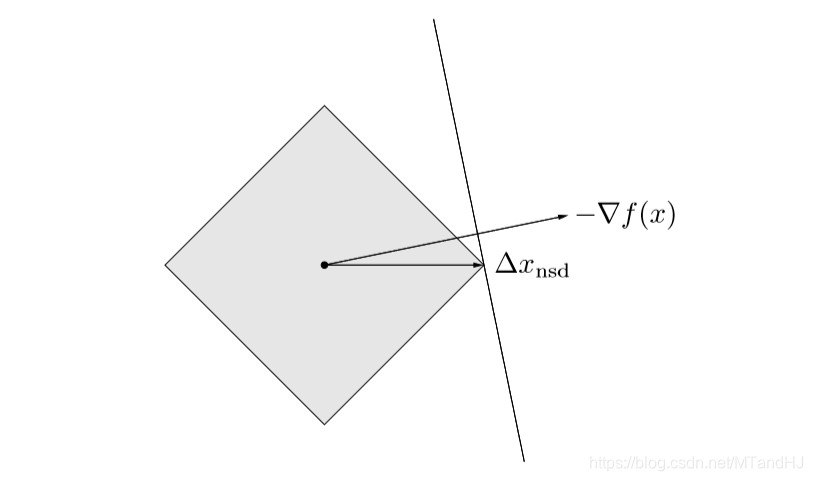
至于收敛性分析，与先前的相反，我们不在这里给出（打起来太麻烦了实际上，有需求直接翻书就好了）。
数值试验
我们依然选择\(f(x)=e^{x_1+3x_2-0.1}+e^{x_1-3x_2-0.1}+e^{-x_1-0.1}\)，\(\alpha=0.2,\beta=0.7\)，初始点为\((7, 3)\)，下图为我们展示了一种较为极端的坐标下降的方式。
代码只需要改变gradient2的几行而已。
def gradient2(x):
x0 = x[0]
x1 = x[1]
grad1 = np.exp(x0+3*x1-0.1) \
+ np.exp(x0-3*x1-0.3) \
- np.exp(-x0-0.1)
grad2 = 3 * np.exp(x0+3*x1-0.1) \
-3 * np.exp(x0-3*x1-0.3)
if abs(grad1) > abs(grad2):
return np.array([grad1/abs(grad1),0])
else:
return np.array([0, grad2/abs(grad2)])
Newton 方法
最开始看的时候，还很疑惑，后来才发现，原来这个方法在很多地方都出现过。除了《凸优化》(《Convex Optimization》)，数学分析（华师大）和托马斯微积分都讲到过。虽然，或者将的一元的特殊情况，而且，后者的问题是寻找函数的零值点。起初，还不知道怎么把俩者联系起来，仔细一想，导函数的零值点不就是我们所要的吗？当然，得要求函数是凸的。
实际上，Newton方法是一种特殊的二次范数方法。特殊在，\(P\)的选取为Hessian矩阵\(\nabla^2 f(x)。\)我们还没有分析，二次范数的\(P\)应该如何选择。在下降方法的收敛性分析中，我们强调了条件数的重要性。加上刚刚分析过的坐标变换，坐标变换后，新的Hessian矩阵变为：
所以，如果我们取\(P =\nabla^2f(x^*)\)，那么新的Hessian矩阵在最有点附近就近似为\(I\)，这样就能保证快速收敛。如果，每次都能选择\(P=\nabla^2 f(x)\)，这就是Newton方法了。下图反映了为什么这么选择会加速收敛：
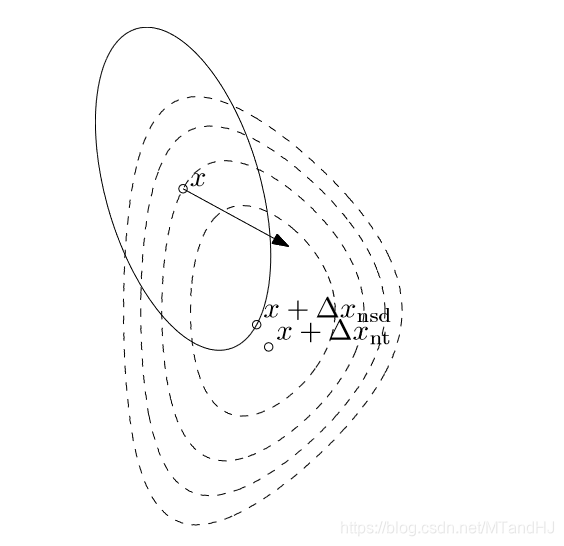
Newton 步径
Newton步径：
则：
因为我们假设Hessian矩阵正定，所以上述不等式在\(\nabla f(x) \ne 0\)时都成立。
二阶近似的最优解
\(f(x+v)\)在\(v=0\)处的二阶近似为：
这是\(v\)的二次凸函数，在\(v=\Delta x_{nt}\)处到达最小值。下图即是该性质的一种形象地刻画：
线性化最优性条件的解
如果我们在\(x\)附近对最优性条件\(\nabla f(x^*)=0\)处进行线性化，可以得到：
这个实际上就是我在最开始对Newton方法的一个解释。不多赘述。
Newton 步径的仿射不变性
这个在代数里面是不是叫做同构？
Newton 减量
我们将
称为Newton减量。
有如下的性质：
Newton步径同样是仿射不变的。
Newton步径常常用作停止准则的设计。
Newton 方法
算法如下：
收敛性分析
收敛性分为俩个阶段，证明比较多，这里只给出结果。
第一阶段为阻尼Newton阶段，第二阶段为二次收敛阶段。
数值实验
我们依然选择\(f(x)=e^{x_1+3x_2-0.1}+e^{x_1-3x_2-0.1}+e^{-x_1-0.1}\)，\(\alpha=0.2,\beta=0.7\)，初始点为\((7, 3)\)，下图采用牛顿方法的图（代码应该没写错吧）。
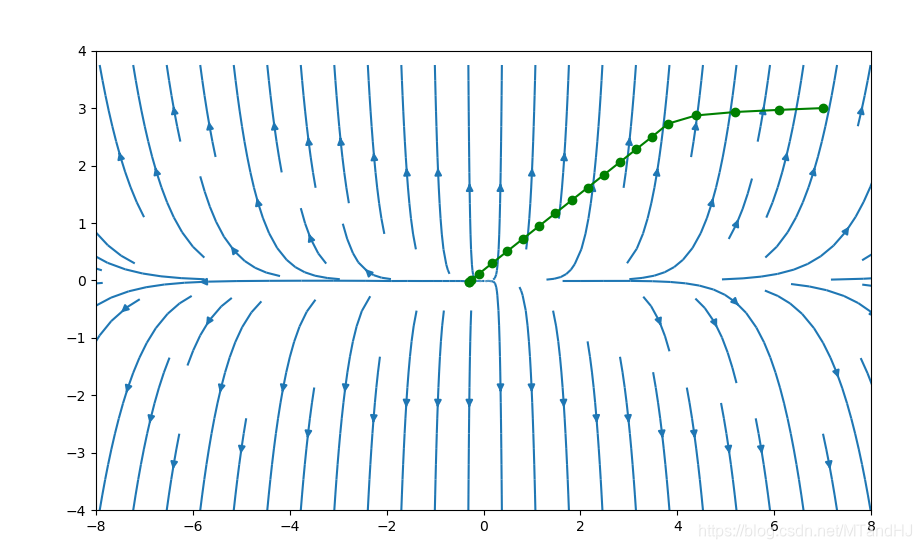
下图初始点为\((-5, 3)\)
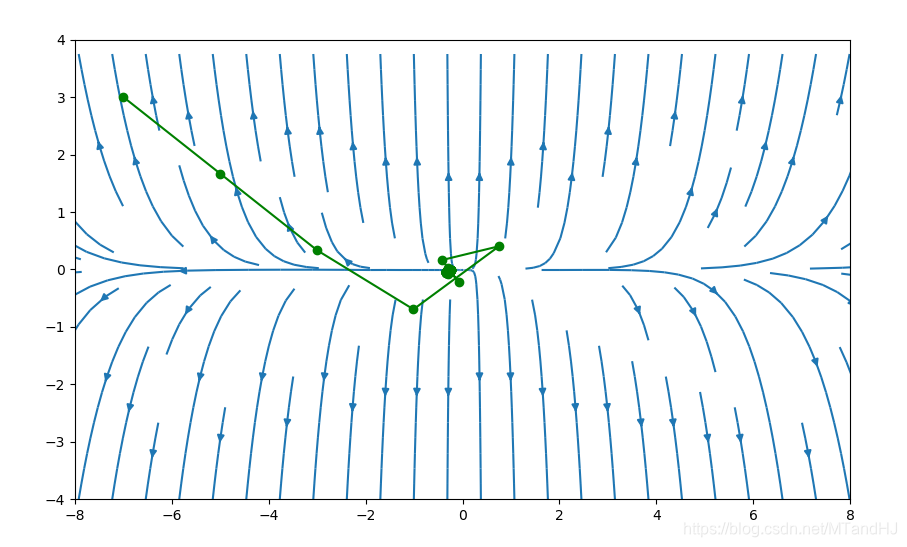
代码
def hessian(x):
x0 = x[0]
x1 = x[1]
hessian = np.zeros((2, 2), dtype=float)
element1 = np.exp(x0 + 3 * x1 - 0.1)
element2 = np.exp(x0 - 3 * x1 - 0.1)
element3 = np.exp(-x0 - 0.1)
hessian[0, 0] = element1 + element2 + element3
hessian[0, 1] = 3 * element1 - 3 * element2
hessian[1, 0] = 3 * element1 - 3 * element2
hessian[1, 1] = 9 * element1 + 9 * element2
return np.linalg.inv(hessian)
下降方法也修改了一下：
def grad3(self, gradient, alpha, beta, error=1e-5):
"""回溯直线收缩算法 Newton步径
gradient: 梯度需要给出
alpha: 下降的期望值 (0, 0.5)
beta:每次更新的倍率 (0, 1)
error: 梯度的误差限，默认为1e-5
"""
assert hasattr(gradient, "__call__"), \
"Invalid gradient"
assert 0 < alpha < 0.5, \
"alpha should between (0, 0.5), but receive {0}".format(alpha)
assert 0 < beta < 1, \
"beta should between (0, 1), but receive {0}".format(beta)
error = error if error > 0 else 1e-5
def search_t(alpha, beta, grad, hessian_inv):
"""回溯"""
t = 2
t_old = 2
step = grad @ hessian_inv
grad_module = grad @ step
assert grad_module >= 0, "wrong in grad_module"
while True:
newx = self.x + t * step
newy = self.__f(newx)
if newy < self.y - alpha * t * grad_module:
return t_old
else:
t_old = t
t = t_old * beta
while True:
grad = -gradient(self.x)
hessian_inv = hessian(self.x)
t = search_t(alpha, beta, grad, hessian_inv)
x = self.x + t * grad @ hessian_inv
lam = grad @ hessian_inv @ grad
if lam / 2 < error: #判别准则变了
break
else:
self.x = x
self.y = self.__f(self.x)
self.__process.append((self.x, self.y))
