Spectral Bounds for Sparse PCA: Exact and Greedy Algorithms[贪婪算法选特征]

概括
这篇论文,不像以往的那些论文,构造优化问题,然后再求解这个问题(一般都是凸化)。而是,直接选择某些特征,自然,不是瞎选的,论文给了一些理论支撑。但是,说实话,对于这个算法,我不敢苟同,我觉得好麻烦的。
Sparse PCA Formulation
非常普遍的问题
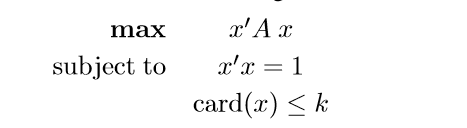
Optimality Conditions
这一小节,论文给出了,上述问题在取得最优的情况下应该符合条件。
条件1
如果是上述问题的最优解,那么(由非零元组成)是子举证(非零元所在位置,的行列)的主特征向量。
这个条件是显然的。
条件2
感觉和上面也没差啊。

Eigenvalue Bounds
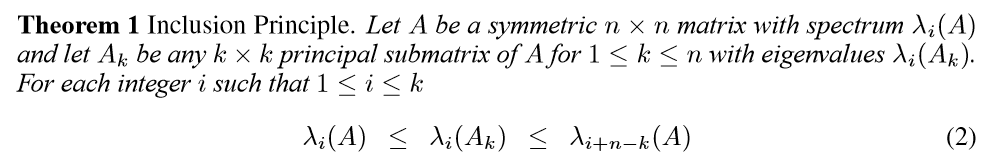
这个定理,可以由一个事实导出:
为一对称矩阵,为其特征值,且降序排列。
为的任意级主子式,为其特征值,那么有下面分隔:
根据这个事实,再用归纳法就可以推出上面式子。
分隔定理的证明(《代数特征值问题》p98)
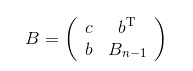
存在正交变换,使得右下角变为对角阵。若正交矩阵使得为对角阵,那么,
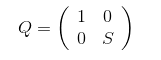
且右下角矩阵的特征值并没有变化。
令:
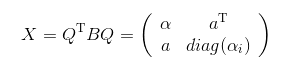
设只有个成分不为0,若,那么就是的特征值。
经过一个适当的置换矩阵变换,我们可以得到:
(注意,下面的和上面的不是一个,只是为了与书上的符号相一致)
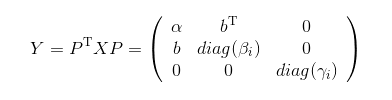
那么只需要考虑
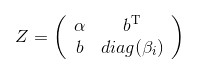
的特征值就行了,因为是矩阵和所共有的。
考虑的特征多项式:
假定中只有个不同的值,不失一般性,可令它们为,
且重数为
等式左端有因子:
因此,为的特征值,重数为
等式除以可得:
的剩余的特征值是的根。
根据正负的特点,和连续函数(实质上是分段的)根的存在性定理,可以知道
的个根满足:
这样所有根的序列就得到了,就是我们要证的。整理一下可以得到,
除了刚刚讲的个根,
还有个相同的特征值,以及
个.
另外一个性质
这个性质不想去弄明白了
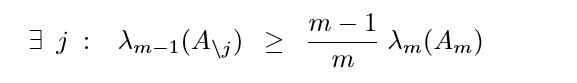
算法
我的理解这样的:
step1.选第一个特征,就是对角元最大的那个
step2.在第一个的基础上,再选一个,这次会形成一个的子矩阵,所以,需要选择令这个矩阵首特征值最大的第二个特征。
step3.反复进行,直到k?
这是前向的,还有对应的后向的,一个个减。论文推荐是,俩种都进行,然后挑二者中比较好的一个。
未免太复杂了些?
代码
只写了前向的代码:
import numpy as np
def You_eig_value(C): #幂法 只输出特征值
d = C.shape[1]
x1 = np.random.random(d)
while True:
x2 = C @ x1
x2 = x2 / np.sqrt(x2 @ x2)
if np.sum(np.abs(x2-x1)) < 0.0001:
break
else:
x1 = x2
return x1 @ C @ x1
def forward(C):
n = C.shape[0]
label1 = set(range(n))
label = [np.argsort(np.diag(C))[-1]]
label1 -= set(label)
count = 0
while len(label1) > 0:
count += 1
maxvalue = 0
maxi = -1
for i in label1:
value = You_eig_value(C[label+[i],:][:,label + [i]])
if value > maxvalue:
maxvalue = value
maxi = i
label.append(maxi)
label1 -= {maxi}
return label
f = open('C:/Users/biiig/Desktop/pitprops.txt')
C = []
for i in f:
C.append(list(map(float, i.split())))
f.close()
C = np.array(C)
forward(C) # [12, 6, 5, 9, 1, 0, 8, 7, 3, 2, 11, 4, 10]




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 【自荐】一款简洁、开源的在线白板工具 Drawnix