Generalized Power Method for Sparse Principal Component Analysis
引
关于稀疏主成分,作者提了俩种收缩算法和俩种块方法,主要依赖\(\ell_0\)和\(\ell_1\)惩罚项. 主要思想是将通过求解优化问题,找到合适的\(P\), 其中的元素为\(\{0, 1\}\), 即指示载荷向量那些部分应该非零. 然后再通过迭代求解合适的载荷向量, 不过我觉得按照其理论,分明在求解\(P\)的时候顺带也可以将载荷向量\(Z\)也一并求得,可是却绕了一个弯,虽然也有其道理.
主要内容
收缩方法 \(\ell_1\)惩罚项
这部分,考虑的是如下的优化问题:
其中\(\Sigma=A^TA, A \in \R^{p \times n}\)(\(p\)个样本,\(n\)为样本维度)为协方差矩阵,而\(\mathcal{B}^n = \{y \in \R^n | y^Ty \le 1 \}\). 这个的意思蛮明显的,就是希望添加一个\(\ell_1\)惩罚项,使得\(z\)能够稀疏化,通过如下转化:

其中\(z_i'=\mathrm{sign}(a_i^Tx)z_i'\).
(5)的推导是这也的,对于固定的\(z\), \(x=Az / \|Az\|\)为最优解,等式自然可得. 因为俩个\(\max\)所代表的可行解域是一致的,所以可以交换位置.
如果固定\(x\),那么关于\(z\)的最优解为:

如何思考呢,首先看(6), 我们要做的是分配\(z_i\), 但是,为了最大化,显然\((|a_i^Tx|-\gamma)\le 0\)的部分是不配得到分配的,所以我们可以假设\(z_i,i=1,2,\ldots, n' \le n\)非0, 利用拉格朗日乘子法:
其中\(t_i=|z_i|\), 易证: \(t_i=(\gamma - |a_i^Tx|) / 2\lambda\), 所以\(|z_i|\)的大小和\(\gamma - |a_i^Tx|\)成比例,(7)的结论不言而喻.
这样子,问题(6)就转换为下面的问题:
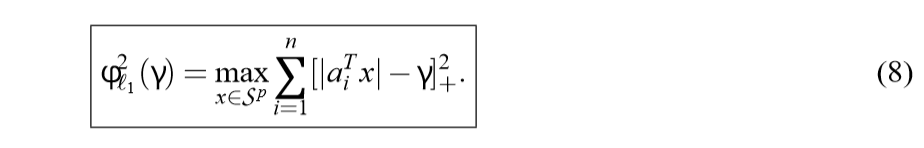
其中\(\mathcal{S}^p = \{y \in \R^p | y^Ty=1\}\).
也就是说,最后这类问题的求解可以转化为,先通过问题(8)找到最优的\(x\), 再利用(7)求解\(z\). 但是,作者最后是通过(8), 找到\(x\), 再通过\(|a_i^T x| - \gamma\) 判断\(z\)中那些元素非零,再去掉\(\ell_1\)惩罚项,再求解一次优化问题. 我真的很疑问,这个操作有必要吗,的确,听起来很合理,但是\(\ell_1\)本身就具有稀疏化的特性,为何非要如此呢?
另外,需要指出,\(\gamma\)应当满足一些条件,不然可能导致\(|a_i^T x| < \gamma\)对于所有的\(i\)和\(x\).
收缩方法\(\ell_0\)惩罚项
考虑如下问题:
可以转换为:
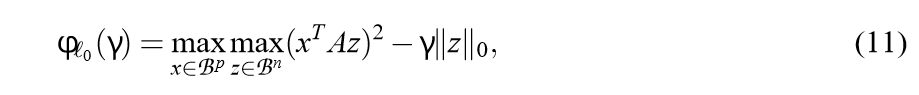
固定\(x\), \(z\)的解为:
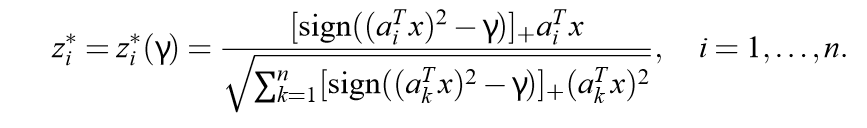
这个部分,二维(\(n=2\))的情况是能够证明, 其它的时候不晓得该怎么证明.
如此,我们同样转化为求解关于\(x\)的问题:
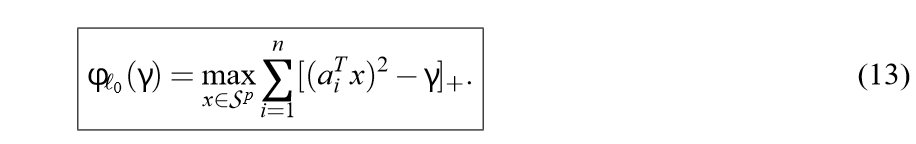
块方法\(\ell_0\)惩罚项
直接给出公式和相应的转化了.
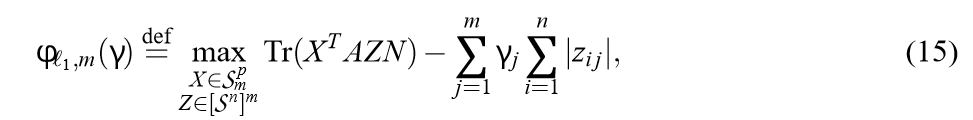
其中\(N\)是一个对角矩阵,也可以做权重来理解, \(\mathcal{S}_m^p = \{Y \in \R^{p \times m}| Y^TY=I_m \}\), \([\mathcal{S}^n]^m=\{Y \in \R^{n \times m} | diag(Y^TY)=I_m\}\).
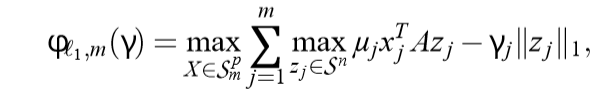

块方法\(\ell_0\)惩罚项
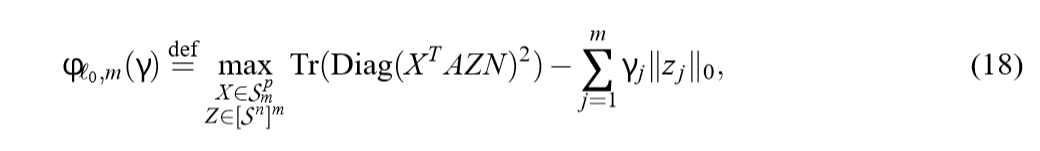
转换如下:
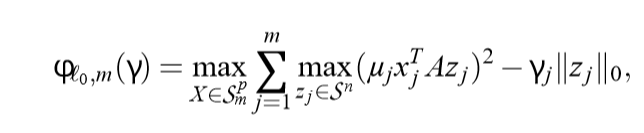
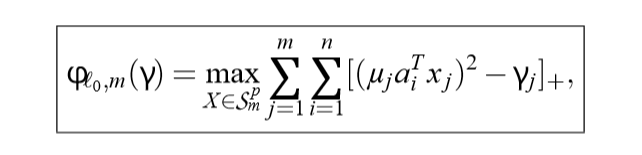
算法




求得\(P\)后,作者考虑如下的问题:
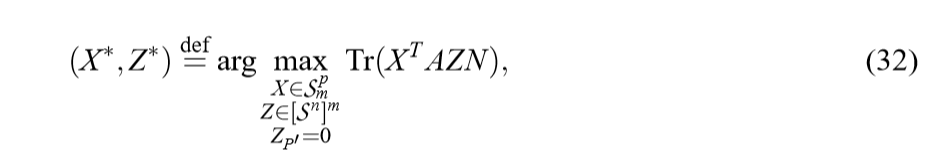
并利用如下的算法求解:



