上下界网络流
•参考资料
[1]:上下界网络流学习笔记
[2]:上下界网络流问题
[3]:上下界网络流
•无源汇的上下界网络流
•模型:
一个网络,求出一个流,使得每条边的流量$x_{i} \in [L_{i},R_{i}]$ ,每个点必须满足总流入量=总流出量(流量守恒)(这个流的特点是循环往复,无始无终)
•构图:
重在处理下界的限制。
对于一条边 $u->v$,下界为$l$,上界为$r$。我们可以将这条边变为上界为$r-l$,下界为$0$。
相当于在可行流的基础上每条边的流量都减小了$l$。但是这样做了之后,流量却不守恒了。
流入$v$的流量少了$l$,流出$u$的流量也少了$l$。
所以要增加一个叫附加流的东西,使得这个附加流和我们的初始流合并之后满足流量守恒
即:
如果某个点在所有边流量等于下界的初始流中满足流量守恒,那么这个点在附加流中也满足流量守恒,
如果某个点在初始流中的流入量比流出量多$x$,那么这个点在附加流中的流出量比流入量多$x$.
如果某个点在初始流中的流入量比流出量少$x$,那么这个点在附加流中的流出量比流入量少$x$.
$x的值$可以枚举x的所有连边求出。比较方便的写法是开一个数组$du[]$,在输入边的时候,对于出点$u$,$du[u]-=l$,对于入点$v$,$du[v]+=l$
$du[i]$表示i在初始流中的流入量-流出量的值,那么$du[i]$的正负表示流入量和流出量的大小关系
建立一个超级源点$S$和超级汇点$T$,然后枚举所有的点$i$,
如果$du[i]<0$,则加$(i,T,-du[i])$,如果$du[i]>=0$,则加$(S,i,du[i])$
然后跑最大流,如果满流(也就是跑完最大流后所有正向边都为0)是可行的,否则不可行
最后,每条边在可行流中的流量=容量下界+附加流中它的流量(即跑完dinic之后所加反向边的权值).
•例题
【题目】
给$n$个点及$m$根管子,每根管子连接两个点可单向运输液体,每时每刻每根管子流进来的物质要等于流出去的物质,$m$条管子组成一个循环体,里面流躺物质。
并且满足每根管子一定的流量限制,范围为$[L_{i},R_{i}]$.即要满足每时刻流进来的不能超过$Ri$,同时最小不能低于$L_{i}$。问是否可行,可行则输出一组可行解。
【思路】
在输入边的时候,对于出点$u$,$du[u]-=l$,对于入点$v$,$du[v]+=l$
建立一个超级源点$S$和超级汇点$T$,然后枚举所有的点$i$,
如果$du[i]<0$,则加$(i,T,-du[i])$,如果$du[i]>=0$,则加$(S,i,du[i])$
然后跑最大流,如果满流(也就是跑完最大流后所有正向边都为0)是可行的,否则不可行
最后,每条边在可行流中的流量=容量下界+附加流中它的流量(即跑完dinic之后所加反向边的权值).
【代码】
•有源汇的上下界最大流
•模型:
现在的网络有一个源点ss和汇点tt,求出一个流使得源点的总流出量等于汇点的总流入量,其他的点满足流量守恒,而且每条边的流量满足上界和下界限制.在这些前提下要求总流量最大.
•构图:
由于源点和汇点的存在使整个网络不满足流量守恒了,那是否可以对源点和汇点操作一下,再变回流量守恒?
可以的!连一条汇点tt到源点ss的边,这条边的流量为INF。由于源点的总流出量等于汇点的总流入量,所以整个网络又循环起来了。
也就可以转化成无源汇的上下界网络流了。于是套用无源汇的上下界网络流,建立超级源点$s$,超级汇点$t$,也就可以得到有源汇的上下界的可行流了。
但此时只是可行却不一定是最大的,那如何去求最大呢?
删去超级源点$s$和超级汇点$t$,在残留网络上跑最大流!(令$s=ss,t=tt$删去超级源点超级汇点,用在ss-tt上跑最大流)
因为第一次最大流只是求得所有满足下界的流量,而残留网络$(ss,tt)$路上还有许多自由流(没有和超级源点和超级汇点连接的边)没有流满,
所以最终得到的最大流=第一次流满下界的流+第二次能流通的自由流。
•例题
【题目】
一个人给$m$个人拍照,计划拍照$n$天,第$i$天给$C_{i}$个人拍照,每天拍照数不能超过$D_{i}$张,而且给每个人i拍照有数量限制$[L_{i},R_{i}]$,
对于每个人$j$,$n$天的拍照总和不能少于$G_{j}$,如果有解求最多能拍多少张照,并求每天给对应的人拍多少张照;没有可能输出-1。
【思路】
设一个源点$s$,$s$到第$i$天连一条上界为$D_{i}$下界为$0$的边,
每个人$j$到汇点连一条下界为$G_{j}$上界为无穷的边,
对于每一天,当天到第$i$个人连一条$[L_{i},R_{i}]$的边。
汇点$t$向源点$s$连一条INF的边,使得网络循环起来
设一个超级源点$ss$和超级汇点$tt$,然后枚举所有的点,
如果$du[i]<0$,则加$(i,tt,-du[i])$,如果$du[i]>=0$,则加$(ss,i,du[i])$
然后跑最大流,如果满流(也就是跑完最大流后所有正向边都为0)是可行的,否则不可行
再删去超级源点和超级汇点,跑最大流
最终得到的最大流=第一次流满下界的流+第二次能流通的自由流。
注意此题要按所给顺序输出
【代码】
•有源汇的上下界最小流
•模型:
现在的网络有一个源点s和汇点t,求出一个流使得源点的总流出量等于汇点的总流入量,其他的点满足流量守恒,而且每条边的流量满足上界和下界限制.在这些前提下要求总流量最小.
•构图:
依然是先跑出一个有源汇可行流.这时候的流也不一定是最小的.
假如我们能在残量网络上找到一条s-t的路径使得去掉这条路径上的流量之后仍然满足流量下限,我们就可以得到一个更小的流.
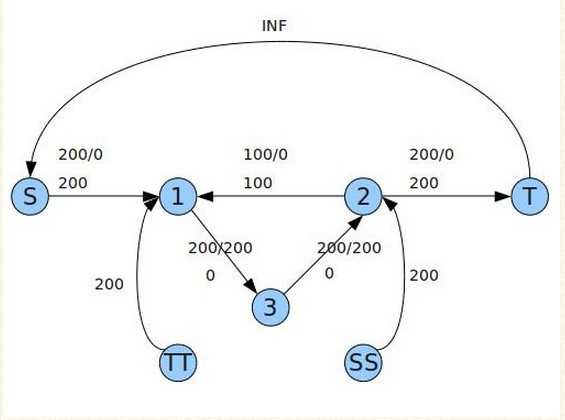
如图转化成有源汇可行流得到的下界流(也就是最小流)是200 $(S$->$1$->$3$->$2$->$T$->$S)$
但是此图的实际最小流是100,问题出在原图中存在环(循环流),而我们没有利用,导致流增大了。
解决方法:先不增加 $t$->$s$ 容量为无穷的边,进行一次最大流,
如果还没有满流,则加一条 $t$->$s$ 容量为无穷的边,再进行一次最大流,
当且仅当所有附加弧满载时,有可行解,解为e[(t->s)^1].w(即t到s的后悔边权值)。
•理解:
有源汇的最小流与最大流的构图区别就在于:
最小流:先建立超级源汇跑一遍无源汇上下界最大流,然后增加 $t$->$s$ 容量为无穷的边跑最大流
最大流:增加 $t$->$s$ 容量为无穷的边并取超级源点超级汇点跑最大流,删去超级源点超级汇点跑最大流
•例题
【题目】
有一个加工生产的机器,起点为$1$终点为$n$,中间生产环节有货物加工数量限制,输出$u\ v\ z\ c$,描述一个加工环节,当$c$等于$1$时表示这个加工的环节必须对纽带上的货物全部加工(即上下界都为z),$c$等于$0$表示加工上界为$z$,下界为$0$,起点最少需要投放多少货物才能传送带正常工作。
【思路】
先建立超级源汇跑一遍无源汇上下界最大流,然后增加 $t$->$s$ 容量为无穷的边跑最大流
【代码】