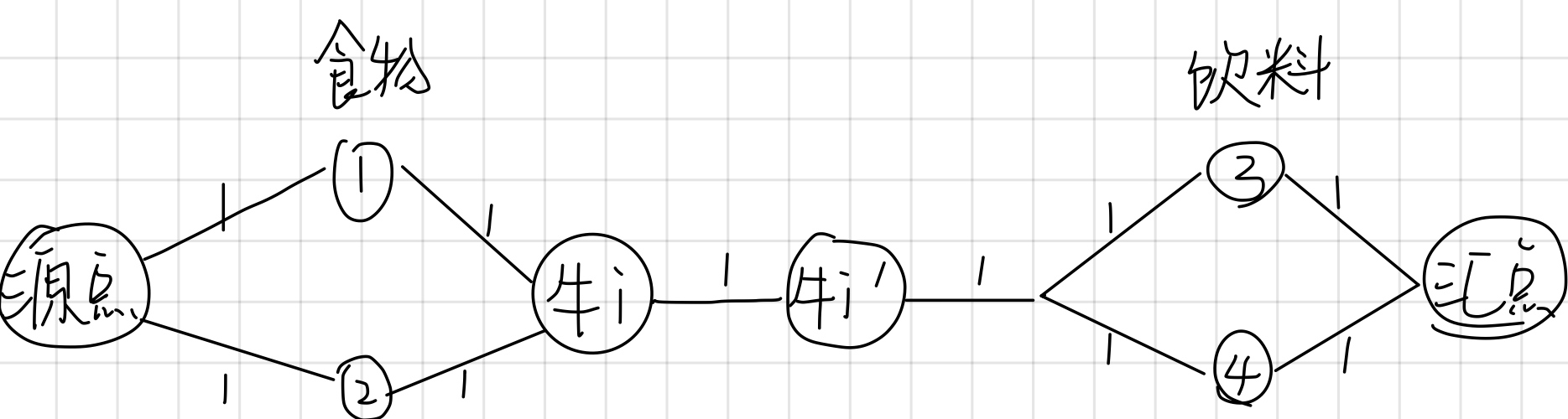网络流建模汇总
•前言
最近在看 Edelweiss 的网络流建模汇总
来学习网络流的建模技巧
毕竟网络流的题难点就在于如何建图，其余大部分就是套路了
于是也写下自己的想法和思路
(虽然一直在借鉴大佬思路)
•最大流
•POJ 1149 Pigs
【题目大意】
有 M 个猪圈，每个猪圈里初始时有若干头猪pig[i]。一开始所有猪圈都是关闭的。依次来了 N 个顾客，每个顾客分别会打开指定的几个猪圈，从中买若干头猪。每 个顾客分别都有他能够买的数量的上限。每个顾客走后，他打开的那些猪圈中的 猪，都可以被任意地调换到其它开着的猪圈里，然后所有猪圈重新关上。问总共 最多能卖出多少头猪。（1 <= N <= 100, 1 <= M <= 1000）
【思路】
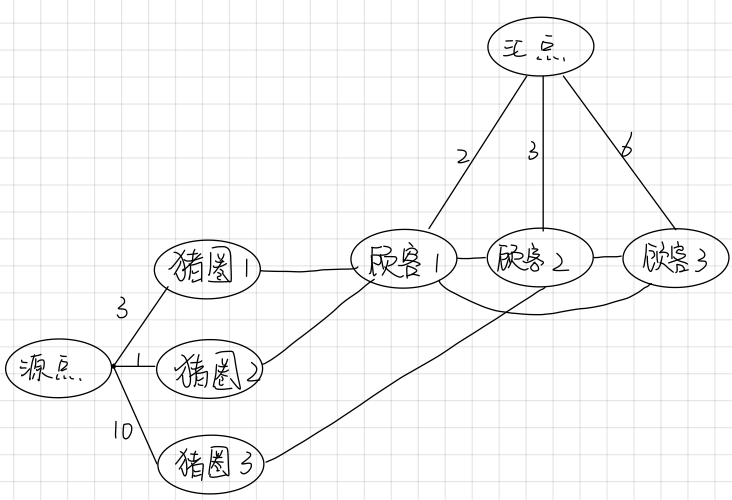
设一个s点为源点，一个t点为汇点
每来一个顾客$m+i$(顾客从m+1开始编号)，如果他所拥有钥匙的猪圈还未被打开过，那连一条源点和他 流量为此猪圈的猪的数量$(s,i,pig[i])$的边
如果他所拥有钥匙的猪圈$index$被打开过，那连一条前一个打开的人和他 流量为INF的边$(vis[index],i,INF)$
每个顾客与汇点连一条流量为此顾客购买力的边$(m+i,t,buy)$
其实就是把可以调换的猪圈混合在了一起，s-t流和调换猪对应了起来
【样例】
3 3
3 1 10
2 1 2 2
2 1 3 3
1 2 3
7
【代码】
•POJ 3281 Dining
【题目大意】
有 F 种食物和 D 种饮料，每种食物或饮料只能供一头牛享用，且每头牛只享用一 种食物和一种饮料。现在有 N 头牛，每头牛都有自己喜欢的食物种类列表和饮 料种类列表，问最多能使几头牛同时享用到自己喜欢的食物和饮料。（ 1 <= F <= 100, 1 <= D <= 100, 1 <= N <= 100）
【思路】
以往一般都是左边一个点集表示供应并与源相连， 右边一个点集表示需求并与汇相连。现在不同了，供应有两种资源，需求仍只有 一个群体，
根据这个群体与两种资源的联系来看，食物和饮料之间并没有直接联系，而是牛与食物，牛与饮料分别有联系
可以把牛放在两种资源中间，源点与食物相连，饮料与汇点相连，然后牛在中间食物与牛相连 牛与饮料相连（t->食物->牛->饮料->汇点）
但是会出现一只牛吃多种食物多种饮料的情况所以要把牛拆点拆成（牛，牛'，1）为了保证只能吃一次，两者之间流量为1
【样例】
4 3 3
2 2 1 2 3 1
2 2 2 3 1 2
2 2 1 3 1 2
2 1 1 3 3
3
->
一只牛会吃多个套餐 一只牛只能吃一个套餐
【代码】
•JOJ 2453 Candy
【题目大意】
有$N$颗糖果和$M$个小孩，老师现在要把这$N$颗糖分给这$M$个小孩。每个小孩$i$对每颗糖$j$都有一个偏爱度$A_{ij}$，如果他喜欢这颗糖$A_{ij} = 2$，否则 $A_{ij} = 1$。小孩$i$觉得高兴当且仅当$∑C_{ij}×A_{ij} >= B_{i}，j=1,2,…,N$，若他分得了糖 $j$,$C_{ij} = 1$否则$C_{ij} = 0$。问能否合理分配这$N$颗糖，使得每个小孩都觉得高兴。（$1 <= N <= 100,000$, $1 <= M <= 10, 0 <= B_{i} <= 1,000,000,000$）
【思路】
一种最直观的想法就是每颗糖 i 作为一个点并连边(s, i, ?)，每个小孩 j 作为一个 点并连边(j, t, Bj)。若小孩 j 喜欢糖果 i 则连边(i, j, 2)，否则连边(i, j, 1)，然后求一 次最大流看是否等于∑Bj，但是源点和糖之间的流量无法确定，为什么呢？因为一旦选定一条边之后就只能从这条边流而不能再进入其他的出边
假设流量为1，那如果小孩喜欢此糖的话，流量需要为2，所以pass!
假设流量为2，如果小孩不喜欢的话，流量需要为1，且不能再流向其他小孩了，为2的话就不能保证不再流量另一个不喜欢的小孩，所以pass!
现在转换一下思路，由于问的是否所有孩子都能高兴，为了尽量让孩子高兴，所以每颗糖都会分出去,即$C_{ij} = 1$
假设有$x$个$A_{ij}=2$,其余$A_{ij}=1$，则 $∑C_{ij}×A_{ij} =∑1*A_{ij}=N+x$，则所有小孩都高兴即为$N+x>=∑B$j
所以只考虑可以额外提供1点高兴值的糖果和小孩，因为贡献值从2变为1减半了，所以小孩到汇点的流量也需要减半，
(达到快乐就行了 不能让他多吃了糖果 还有其他小孩呢)
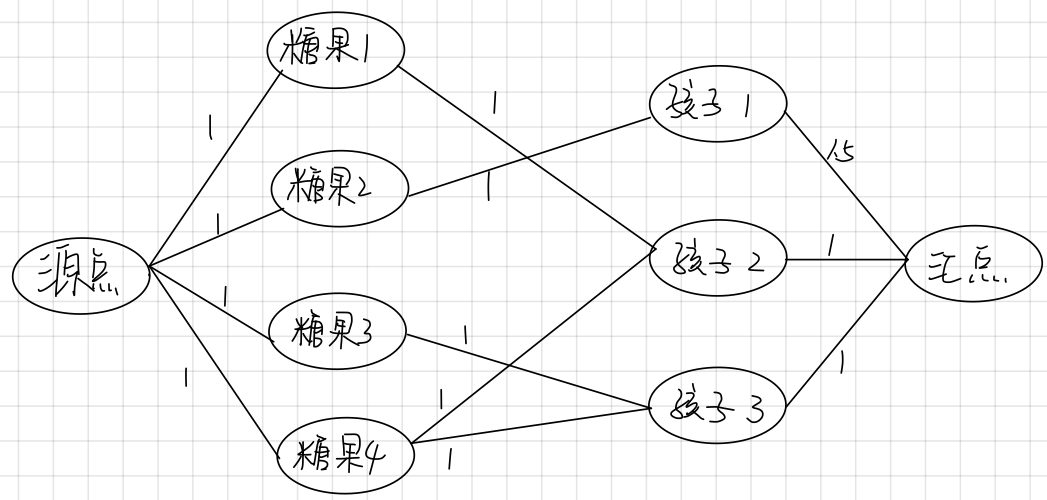
这样就只需要判断小孩是不是喜欢这块糖了，如果喜欢的话，就连边流量为1，如果不喜欢的话就不连边，或者流量为0也行
【样例】
1
4 3
1 2 1
2 1 1
1 1 2
1 2 2
3 2 2
1 1
YES
【代码】
•ZOJ 2760 How Many Shortest Path
【题目大意】
给定一个带权有向图 G=(V, E)和源点 s、汇点 t，问 s-t 边不相交最短路最多有几 条。（1 <= N <= 100）
【思路】
分别以源点和汇点为起点跑dijkstra，得到最短路图，令最短路的边流量都为1，在最短路上跑最大流，得到独立路径条数
类似于hdu 6852，不过最短路图加边时令流量为1
•WOJ 1124 Football Coach
【题目大意】
有 N 支球队，互相之间已经进行了一些比赛，还剩下 M 场没有比。现在给出各 支球队目前的总分以及还剩下哪 M 场没有比，问能否合理安排这 M 场比赛的结 果，使得第 N 支球队最后的总分大于其他任何一支球队的总分。已知每场比赛 胜者得 2 分，败者 0 分，平局则各得 1 分。（1 <= N <= 100, 0 <= M <= 1000）
【思路】
首先利用贪心的思想，让第N支球队赢剩下的所有他参加的比赛，如果此时仍有球队的总分大于等于球队 N 的总分$score[N]$，则已经不可能满足要求；
如果满足的话，想要N赢，那其他的球队i的得分肯定比$score[N]$小，对于除与N以外球队来说，设现在第i支球队得分为$score[i]$,所有比赛结束后得分为$score[i']$
即$score[i']<score[N]$,$score[i']$最大为$score[N]-1$,所以最多再赢$score[N]-score[i]-1$分,也就是每支球队到汇点的容量为$score[N]-score[i]-1$
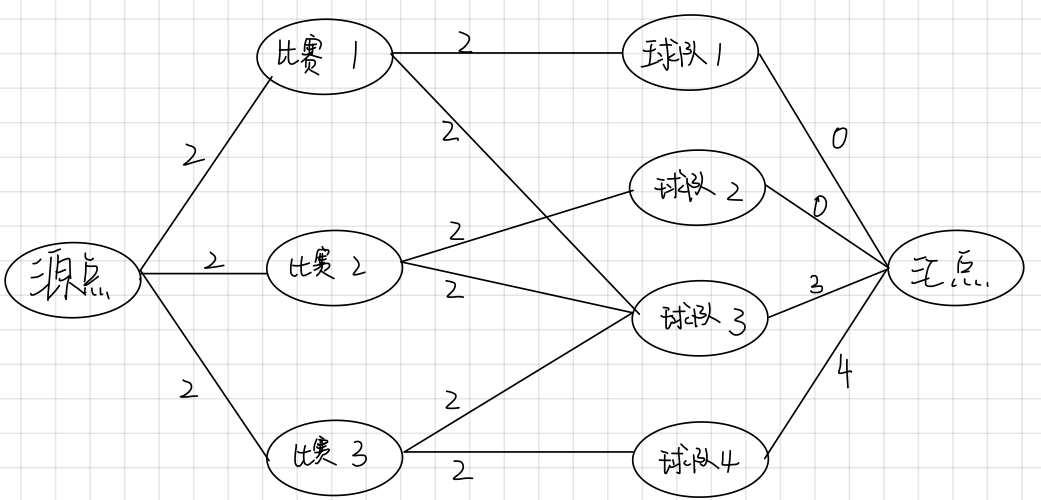
对于除与N相关以外的比赛来说，源点到比赛j的容量为2,(s,j,2),每场比赛向与其关联的两支球队 u, v 连边(j, u, 2), (j, v, 2)
【样例】
5 4
4 4 1 0 3
1 3
2 3
3 4
4 5
NO
•SGU 326 Perspective
【题目大意】
NBA 某小组内有 N 支球队，小组内以及小组间已经进行了若干场比赛。现在给 出这 N 支球队目前胜利的场数、还剩多少场没有比（包括小组内和小组间）以 及小组内任意两支球队之间还剩多少场没有比，问能否合理安排剩下的所有比赛， 使得球队 1 最后成为小组冠军或者并列冠军。 （2 <= N <= 20, 0 <= x <= 10000, x 表示其他任何输入）
【思路】
跟上面WOJ 1124 Football Coach差不多，先令与球队1相关的赛事都让球队1赢，由于想让1赢，那么应该尽可能加大其他队与1的差距 ，
所以令除1以外的小组间的赛事都输，注意这个是可以并列，所以每支球队到汇点的容量为$score[N]-score[i]$
所有小组内的比赛 i（不包括与球队 1 相关的比赛）作为一个点并加边$(s, i, num[i])$，每支球队（不包括球队 1）作为一个点并加边$(j, t, score[N]-score[i])$，每场 比赛向与其关联的两支球队 u, v 连边$(i, u, ∞), (i, v, ∞)$。至于其他球队小组间的 比赛，直接让他们输掉就好，不用管。若最大流等于$∑num[i]$则可以满足要求。
•SPOJ 287 Smart Network Administrator
【题目大意】
一座村庄有 N 户人家。只有第一家可以连上互联网，其他人家要想上网必须拉 一根缆线通过若干条街道连到第一家。每一根完整的缆线只能有一种颜色。网管 有一个要求，各条街道内不同人家的缆线必须不同色，且总的不同颜色种数最小。 求在指定的 K 户人家都能上网的前提下，最小的不同颜色种数。（1 <= N <= 500）
【思路】
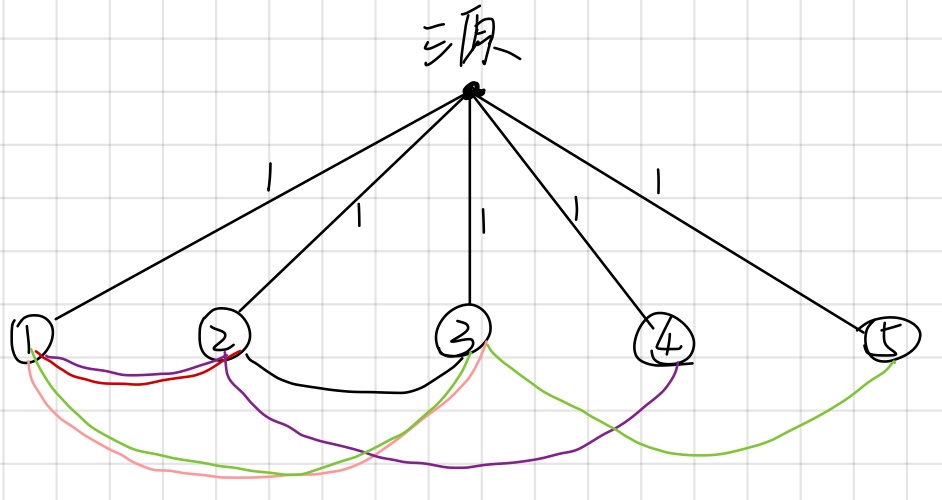
以第一家作为汇点 t，K 户人家中的每一户 i 作为一个点并连边$(s, i, 1)$，对每条街道$(u, v)$，连边$(u, v, c), (v, u, c)，c=∞$。 这样求完最大流后每一条 s-t 流均对应一户人家的缆线，而各条街道内的流量表 示有多少户人家的缆线同时穿过该街道，那么这个流量就是只考虑该条街道的时候最少的不同颜色种数。那么答案是否就是所有街道的不同颜色种数的最大值呢？ 当然不是！最大流只保证总流量最大，而不会去管每条流具体该往哪儿流，所以 这么做不一定能得到最优解。我们只要稍微修改这个模型就一定能保证得到最优 解：去对c进行二分，强制 c 等于某个值 limit，再对网络求最大流，如果等于 K，说明用 c 种不同 的颜色已经足够了；如果小于 K，说明 c 种还不够，还需要往高了调。同时此处 的单调性也很明显：c 越高越容易满足要求。
【样例】
5 5 4
2 3 4 5
1 2
1 3
2 3
2 4
3 54
一种颜色代表一根线，同一根线n种颜色代表流量为n
•SPOJ 962 Intergalactic Map
【题目大意】
在一个无向图中，一个人要从 1 点赶往 2 点，之后再赶往 3 点，且要求中途不 能多次经过同一个点。问是否存在这样的路线。（3 <= N <= 30011, 1 <= M <= 50011）
【思路】
由于是从1到2,再从2到3，可以看做是从2到1,从2到3有没有独立的路径，没有重合的点
为了保持点不重合，我们可以把i点拆开连边$(i,i',1)$，其中$i$点为入点，$i'$点为出点
以2的出点为源点，以0为汇点，为了必须经过1,3点，对1和3的出点和汇点连边$(1',t,1),(3',t,1)$
对于输入的边$(u,v)$，利用入点和出点的关系连接即$(u',v,1),(v',u,1)$
然后判断从源点到汇点的路径是否是两条
最后 输入的时候，可能有边不在1~n的范围内，需要跳过这些边。
【代码】
•最小割
•HOJ 2634 How to earn more
【题目大意】
有 M 个项目和 N 个员工。做项目 i 可以获得 $A_{i}$ 元，但是必须雇用若干个指定的 员工。雇用员工 j 需要花费 $B_{j}$ 元，且一旦雇用，员工 j 可以参加多个项目的开发。 问经过合理的项目取舍，最多能挣多少钱。（1 <= M, N <= 100）
【思路】
蕴含式最大获利问题，最大权闭合子图裸题，戳这
【代码】
•HOJ 2713 Matrix1
【题目大意】
一个 N*M 的网格，每个单元都有一块价值 $C_{ij}$ 的宝石。问最多能取多少价值的宝 石且任意两块宝石不相邻。（1 <= N, M <= 50, 0 <= $C_{ij}$ <= 40000）
【思路】
跟洛谷P2774一样。最大点权独立集裸题，答案=总价值-最小点权覆盖，戳这
【代码】
•ZOJ 2532 Internship
【题目大意】
有 N 个城市，M 个中转站以及 L 条有向边(u, v, c)，表示可以从 u 向 v 传送信息， 带宽为 c。每个城市都在向 CIA 总部发送无穷大的信息量，但是目前总部实际接 收带宽已经不能满足要求。CIA 决定要增大某条边的带宽以增大总部的接收带宽， 请找出哪些边带宽的增加能导致总部接收带宽的增加。（1 <= N+M <= 100, 1 <= L <= 1000）
【思路】
要求找出这样一条边，增加它的容量可以导致最大流的增加。
最直观的办法就是对每一条边增大然后去求最大流，如果最大流增大的话，则符合。但是，复杂度肯定是不神奇的
那要怎么做呢？设t为源点，所有城市和中转站与源点连一条INF的边$(s,i,INF)$,令题目图中的基底为汇点t,然后按照题目中的关系连边
可以先求最大流，得到残留网络，此时残留网络中没有一条可以从源点到汇点流量>0的路。
但是可能有$s->a=x,a->b=0,b->t=y$(其中$x,y$为正整数)的边，如果把$a->b$的边流量增加，就会增大最大流
所以我们需要找出所有可以到达源点s的点 (到达时流量不为0,流量为0是不能到达),所有可以到达汇点的点
可以到达源点的点利用正向边来求，,所有可以到达汇点的点利用反向边求反着求汇点可以到达的点，边权为正才可以到达
可以利用DFS来标记from[i] to[i], true代表可以达到，false则不可以到达
【代码】
•POJ 1815 Friendship
【题目大意】
现代社会人们都靠电话通信。A 与 B 能通信当且仅当 A 知道 B 的电话号或者 A 知道 C 的电话号且 C 与 B 能通信。若 A 知道 B 的电话号，那么 B 也知道 A 的电 话号。然而不好的事情总是会发生在某些人身上，比如他的电话本丢了，同时他 又换了电话号，导致他跟所有人失去了联系。现在给定 N 个人之间的通信关系 以及特定的两个人 S 和 T，问最少几个人发生不好的事情可以导致 S 与 T 无法通 信并输出这些人。如果存在多组解，输出字典序最小的一组。（2 <= N <= 200）
【思路】
由于是最小割点，所以要先拆点(i,i',1)转化成割边，$1~n$为入点，$n+1~2*n$为出点，原图的边按照出点和入点的连接，由于原图边不能割所以设为INF
当且仅当s与t直接相连时，无法割去NO ANSWER!,
先求一次最大流，得到需要割去的点数result，注意为0时不需要输出第二行！(这里没注意一直Wa！)
由于要求最小字典序的，所有从1到n枚举每一个点是否需要割去，由于是从小到大枚举的，所以可以割去时就让他割去，此时字典序最小
何时i可以割去呢?重新建图使(i,i')之间没有边，然后求最小割，若小于result则可以割去
是否割去用vis数组表示，方便后续的建图
【代码】
•Ural 1277 Cops and Thieves
【题目大意】
一个犯罪团伙打算去偷一家美术馆。警察决定派 K 个人堵住所有从匪窝通向美术 馆的道路不过他们只能驻守在沿途顶点处而不能在匪窝或美术馆，且每个点都有一个需要警察驻守的最低人数 Ri。问警察能否完成任务。（2 < N <= 100, 1 < M <= 10000）
【思路】
指定源点汇点的无向图的带权点连通
【代码】
•SPOJ 1693 Coconuts
【题目大意】
N 个城堡守卫正在就非洲的燕子能否搬运椰子而进行投票。每个人都有自己的看法，但是为了避免跟自己的朋友持相反意见，他们 时常会投相反的票。现在给出每个人的初始看法以及朋友关系，求在某种投票方 案下，违背自己意愿的票数与持不同意见的朋友对数的总和最小。 （2 <= N <= 300, 1 <= M <= N(N-1)/2）
【思路】
典型的最小割二者取一式。
二者取其一就是一堆物品，放入两个集合内，放进不同的集合内就会有不同的收益(或代价),使其收益(代价),最大(最小)的一种问题;
将S点设为同意的点，T设为不同意的点。如果$i$同意的话，则加边$(s,i,1),(i,t,0)$,如果$i$不同意，则加边$(s,i,0),(i,t,1)$
同一对好朋友之间连一条容量为1的无向边，代表假设a，b不统一意见。有两种决策，①让a同意b则加$(a,b,1)$ ②让b同意a 则加$(b,a,1)$
【代码】
•hdu 2485 Destroying the bus stations
【题目大意】
给定一个无权有向图 G=(V, E)和源点 s、汇点 t，问最少去掉几个点（连同与其关联的所有边）使得不存在长度小于等于 K 的 s-t 路。$(0 < N <= 50, 0 < M <= 4000, 0 < K < 1000)$
【思路】
如果没有K这个条件，而是只让最短路增大的话，就跟hdu 6852差不多了，都是用根据路径长度对选择出来的路重新构图。有两个地方不同
一个区别是一个有向一个无向。无向的时候在跑最短路就不用区分方向了，这里比6852简化了
另一个区别是一个是最小割，一个是最小割点集。最小割点集需要拆点，这个强化了。
拆点时还是分为入点和出点连边$(i,i',1)$，其他的新边都是$(u+n,v,INF)$
加上K这个条件就不是只让最短路增大了，而是增大到$(>K)$,想6852时怎么挑选的边来构图
dij.dis[1][u]+dij.dis[0][v]+w==dij.dis[1][n]而这里是需要把造成$<=K$的点去掉，所以就需要把条件改成$<=K$
dij.dis[1][u]+dij.dis[0][v]+w<=k还有在构新图的时候不要把边构成无向！
例如：$dis[1->u->v->n]<k$并且$dis[1->v->u->n]<k$,只需加$u->v$或者$u->v$一条边，因为这两个点中割去一个，两条边都会不存在了
如果加成双向边的话，还会有一条存在，就导致错误！
【补充】
hdu上有hack最大流的数据，貌似正解是最小费用最大流，不过我是来练习最大流最小割，所以就不去纠正了
【代码】
View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 #define pii pair<int,int> 4 #define INF 0x3f3f3f3f 5 #define mem(a,b) memset(a,b,sizeof(a)) 6 const int maxn=1e5+5; 7 8 int n,m,s,t; 9 struct Edge 10 { 11 int v; 12 int w; 13 int next; 14 }G[maxn<<1],e[maxn<<1]; 15 int dhead[maxn],dcnt; 16 void addEdge(int u,int v,int w) 17 { 18 G[++dcnt]={v,w,dhead[u]}; 19 dhead[u]=dcnt; 20 } 21 22 struct Dij 23 { 24 int dis[2][maxn]; 25 bool vis[maxn]; 26 priority_queue<pii,vector<pii>,greater<pii> > q; 27 28 void dij(int s,int n,bool ok) 29 { 30 for(int i=1;i<=n;i++) 31 dis[ok][i]=INF,vis[i]=0; 32 33 dis[ok][s]=0; 34 q.push({0,s}); 35 while(!q.empty()) 36 { 37 int u=q.top().second; 38 q.pop(); 39 if(vis[u]) 40 continue; 41 vis[u]=1; 42 for(int i=dhead[u];~i;i=G[i].next) 43 { 44 int v=G[i].v; 45 int w=G[i].w; 46 if(dis[ok][v] > dis[ok][u]+w) 47 { 48 dis[ok][v]=dis[ok][u]+w; 49 if(!vis[v]) 50 q.push({dis[ok][v],v}); 51 } 52 } 53 } 54 } 55 }dij; 56 57 int head[maxn],cnt; 58 void add(int u,int v,int w) 59 { 60 e[++cnt]={v,w,head[u]}; 61 head[u]=cnt; 62 e[++cnt]={u,0,head[v]}; 63 head[v]=cnt; 64 } 65 66 struct Dinic 67 { 68 int cur[maxn],d[maxn]; 69 bool bfs() 70 { 71 queue<int> q; 72 for(int i=0;i<=2*n+1;i++) 73 d[i]=-1; 74 d[s]=0; 75 q.push(s); 76 while(!q.empty()) 77 { 78 int u=q.front(); 79 q.pop(); 80 for(int i=head[u];i!=-1;i=e[i].next) 81 { 82 int v=e[i].v; 83 if(d[v]==-1&&e[i].w>0) 84 { 85 d[v]=d[u]+1; 86 q.push(v); 87 } 88 } 89 } 90 return d[t]!=-1; 91 } 92 93 int dfs(int u,int flow) 94 { 95 int nowflow=0; 96 if(u==t) return flow; 97 for(int i=cur[u];i!=-1;i=e[i].next) 98 { 99 cur[u]=i; 100 int v=e[i].v; 101 if(d[v]==d[u]+1&&e[i].w>0) 102 { 103 if(int k=dfs(v,min(flow-nowflow,e[i].w))) 104 { 105 e[i].w-=k; 106 e[i^1].w+=k; 107 nowflow+=k; 108 if(nowflow==flow) 109 break; 110 } 111 } 112 } 113 if(!nowflow) d[u]=-2; 114 return nowflow; 115 } 116 int din() 117 { 118 int ans=0; 119 while(bfs()) 120 { 121 for(int i=0;i<=2*n+1;i++) 122 cur[i]=head[i]; 123 124 ans+=dfs(s,INF); 125 } 126 return ans; 127 } 128 }_din; 129 130 void Init() 131 { 132 mem(dhead,-1); 133 dcnt=-1; 134 mem(head,-1); 135 cnt=-1; 136 } 137 138 int main() 139 { 140 // freopen("C:\\Users\\14685\\Desktop\\C++workspace\\in&out\\contest","r",stdin); 141 int k; 142 while(~scanf("%d%d%d",&n,&m,&k)) 143 { 144 Init(); 145 s=1+n,t=n; 146 if(!(n+m+k)) 147 return 0; 148 for(int i=1;i<=m;i++) 149 { 150 int u,v; 151 scanf("%d%d",&u,&v); 152 addEdge(u,v,1); 153 addEdge(v,u,1); 154 } 155 dij.dij(1,n,true); 156 dij.dij(n,n,false); 157 for(int u=1;u<=n;u++) 158 { 159 for(int i=dhead[u];~i;i=G[i].next) 160 { 161 if(i&1)///只加单向边 162 continue; 163 int v=G[i].v; 164 if(dij.dis[1][u]+dij.dis[0][v]+1<=k) 165 add(u+n,v,INF); 166 } 167 } 168 169 for(int i=1;i<=n;i++) 170 add(i,i+n,1); 171 172 int ans=_din.din(); 173 printf("%d\n",ans); 174 } 175 }
•费用流
学完费用流发现，貌似最大流的题费用流大部分都能做
•HOJ 2543 Stone IV
【题目大意】
在无向图 G 中，一个人要从源点 $s$ 购买一些石头并运到汇点 $t$。每块石头单价是 $P$ 元。每条边 $i$ 有一个初始容量 $C_{i}$，
当容量超过 $C_{i}$ 时，每增加一单位容量要额外 花费 $E_{i}$ 元。 他现在手头只有 $C$ 元，问他最多能买多少块石头并成功运到目地
【思路】
典凸费用流问题，费用随流的增加呈分段线性状态，可以通过加边的手段转化为最小费用流进行求解。
只需将原图中的每条边$(u, v)$拆成两条： $(u, v, C_{i}, 0), (u, v, ∞, E_{i})$即可。
当最小费用$>C$时，maxflow减去所多出来的流量
【代码】
•HOJ 2739 The Chinese Postman Problem
【题目大意】
带权有向图上的中国邮路问题：一名邮递员需要经过每条有向边至少一次，最后 回到出发点，一条边多次经过权值要累加，问最小总权值是多少。
【思路】
利用欧拉回路来求。
若原图的基图不连通，或者存在某个点的入度或出度为 0 则无解。
统计所有点的 入度出度之差 $D_{i}$，对于 $D_{i} > 0$ 的点，加边$(i, t, D_{i}, 0)$；对于 $D_{i} < 0$ 的点，加边$(s, i, -D_{i}, 0)$；
对原图中的每条边$(i, j)$，在网络中加边$(i, j, ∞, D_{ij})$，其中 $D_{ij}$ 为边$(i, j)$的权值。
求一次最小费用流，费用加上原图所有边权和即为结果。
【代码】
我的代码过不了...从网上扒拉的题解的代码也过不了....
HOJ 2739 The Chinese Postman Problem
