模拟赛总结（四）（终章?）

2024.10.30

2024.10.31

T1 四舍五入

就是求 $i % j < 0.5 j$ 的数量

枚举模数，贡献就是 $[k j, k j + ⌊ \frac{j - 1}{2} ⌋]$ ，差分维护区间加即可

code

T3 道路修建

ps:说的是云淡风轻，机房各大神犇都表示细节过多还很麻烦，后来讲题的人也吐槽了...

T4 逆序图

定义 $F_{i}$ 表示连续 $i$ 个数（即 $k, k + 1, . . ., k + i - 1$ ）在不考虑连通性，只选一条边下的权值和， $G_{i}$ 表示 $i$ 个数 在联通快内的权值和（很明显， $G_{i}$ 表示只选一条边）

我们先考虑一个事情：有多少排列的图是联通的（后面要用）

定义 $f_{i}$ 表示连续 $i$ 个数的排列中连通图数，根据定义，枚举断点 $j$ ，那么 $f_{i - j} \times j!$ 就是非法，意思就是后 $i - j$ 个数联通，前面的瞎搞，这两部分是不联通的，那么

f_{i} = i! - \sum_{j < i} j! f_{i - j}

处理出 $f$ 后，考虑求出 $F$ 或 $G$

求 $F_{i} ：$

对于 $F_{i}$ ，考虑到映射用的函数自变量是排列的差值，所以沿用上面的枚举，然后选定的逆序对就是 $(k, k - j)$ ，函数值为 $W_{j}$ ，一共 $i - j$ 种，对于每个逆序对，都有 $C_{i}^{2} \times (i - 2)!$ 种分布，那么

F_{i} = \sum_{j < i} W_{j} \times (i - j) \times C_{i}^{2} \times (i - 2)!

然后就是题解的结论：排列图的联通快是若干个不相交的区间

那么考虑能否容斥出每个区间的权值和

同样使用求 $f$ 的方法，枚举断点，根据求 $f$ 可知： $[1, j]$ 瞎搞， $[j + 1, i]$ 连通，那么

G_{i} = F_{i} - \sum_{j < i} (G_{i - j} \times j! + F_{j} \times f_{i - j})

就是减去两边区间各自的贡献

定义答案为 $a n s_{i}$ ，那么对于每个可能的区间，要么选( $a n s_{j} \times G_{i - j}$ )，要么不选( $a n s_{j} \times f_{i - j}$ )，要么把它做第一个( $G_{i - j} \times j!$ )

code

2024.11.1

注：可以通过比赛主页得到题面

T2 矩形

注： $S$ 表示 $x$ 坐标相同的点组成的集合，“相交”指的是 $y$ 坐标相同的个数

~~块长越小，码越快~~

code

2024.11.2

暴力： $50 + 50 + 10 + 35$

2024.11.4

~~ f**k the int128 ~~

T3 建筑师

把 $n$ 作为分水岭，那么左右各有 $A - 1, B - 1$ 栋能看见的建筑

把能看见的建筑和被他挡住的看做一组，共 $A + B - 2$ 组。因为能看见的一定在组的边界，所以一组内的分布视为圆排列，使用第一类斯特林数

然后再给一边选出需要的楼，那么答案即：

[\begin{matrix} n - 1 \\ A + B - 2 \end{matrix}] \times (\begin{matrix} A + B - 2 \\ A - 1 \end{matrix})

2024.11.5

T4 银行的源起（banking）

只会 $n^{3}$ 暴力， $n^{2}$ 没去想

$n^{2}$ 的 $30$

code

2024.11.6

T1 新的阶乘

自信满满以为可切，结果 $T$ 俩...

小改成埃筛形式就过了...

code

T2 博弈树

想到直径了，但还是猜错性质qwq

code

T3 划分

暴力倒是到手了...就是有点少...

注1：二分哈希指的是在比对可能的 $n - k + 1$ 长的区间时，二分出最靠左的位置上数字不同的地方，使用哈希比对大小

注2：前缀 $0$ 个数 $\geq k$ 时注意组合数的范围

注3：自然溢出不能使用，只能用取模

注4： corner case特判，不然有两个点过不去

code

T4 灯笼

原题

或者去看谷子题解

含注释

2024.11.7

数据有点水啊。。。

T3 函数（fun）

30pts（实测 $60$ ，还有直接艹过去的。。。）： $O (n^{2})$ 枚举所有情况。

std:

求解 $x_{i} \oplus a$ 最小和最大的两个位置 $c_{1}, c_{2}$ ，如果 $f (c_{1}) \times f (c_{2}) > 0$ 显然无解。

否则每次取 $c_{1}, c_{2}$ 中点 $m i d$ ，因为 $f (c_{1}), f (c_{2})$ 异号，所以 $f (c_{1}), f (m i d)$ 和 $f (m i d), f (c_{2})$ 必然有一对异号，每次区间长度减半，因此重复 $\log$ 次即可。

求解 $x_{i} \oplus a$ 最小和最大的两个位置 $c_{1}, c_{2}$ 可以利用 trie 快速求解，时间复杂度为 $((n + q) (\log n + \log V))$ 。

code

T4 编辑

30pts

枚举 $T$ 的某一子串进行编辑距离求解的DP，具体状态为让 $A$ 变成 $B$ ，现在只考虑 $A [1 : i]$ 变成 $B [1 : j]$ 的编辑距离为 $f [i] [j]$ ，转移时考虑删除，添加，修改第 $i + 1$ 个位置即可，时间复杂度为 $O (n^{4})$ 。

100pts

枚举每个后缀， $f_{i, j}$ 表示最大的 $x$ ，使得 $S [1 : x]$ 和 $T [1 : x + j]$ 可以在 $i$ 次编辑内得到，显然若 $x$ 可以，所有 $x_{0} \leq x$ ， $S [1 : x_{0}]$ 和 $T [1 : x_{0} + j]$ 都可以在 $i$ 次编辑内得到。

考虑如何转移，先考虑做完第 $j$ 次编辑操作后往外延申，可以延申的即为 $S$ 的一个后缀和 $T$ 的一个后缀的最长公共前缀，即 $f_{i, j} = f_{i, j} + LCP (S [f_{i, j} + 1 : | S |], T [f_{i, j} + j + 1 . . : | T |])$ ，随后我们可以通过对 $f_{i + 1, j - 1}, f_{i + 1, j}, f_{i + 1, j + 1}$ 三项进行转移，即考虑下一次的编辑的具体操作是删除添加还是修改。

每次要算的两个后缀的前缀下标不会差超过 $k$ ，因此一共至多求 $O (n k)$ 次 LCP，可以利用二分+ hash 的方式解决。

记录每个后缀中 $f_{i, j} = | S |$ 的那些状态，即可计算出最终答案，时间复杂度为 $O (n k^{2} + n k \log n)$ 。

注1：枚举的 $j$ 可以为负，即 $j \in [- k, k]$ ，所以要坐标平移

注2：LCP指最长公共前缀

90ptsTLE

2024.11.10

T1

tj提到了 $B o r u v k a$ ，不过这题可以直接贪心

一个数只可能和前面的最大值或者后面的最小值连边，这两个可以预处理。然后用若干个最大值将数列分成若干块，每次跳最大值，对块内元素使用上述方式连边即可。注意还要保证连通性，所以每走完一个块就要让当前块内最大和上一个块内最小值连边（倒序扫）

code

T2

可以不用离线，直接线段树对 $1$ 个数的所有情况进行维护，在线区间查询即可，不过有一些细节：

1.为了实现tj中要求 $p o p c o u n t$ 相等的数全部相等，维护的 $v a l$ 使用或合并，这样如果两边的值不同就会使得 $1$ 个数变化，只需要在枚举个数时再次检查 $v a l$ 的 $1$ 个数是否和枚举的个数相同即可
2.注意到 $a_{i} \geq 0$ ，所以可能出现两个党派计算值均为 $0$ 的情况，然而或党初始值也是 $0$ ，所以还要维护两个布尔变量表示两个党派是否放了人， $c h e c k$ 时也要求布尔为1
3.考虑 $p o p c o u n t$ 相同的数如何分配，没有就不分了直接比对，有一个就看给哪边，有一种成立即可。否则两边都要至少分一个

code

T3

先将表达式建成树：所有叶子是变量，其他节点为运算符，运算顺序为从下往上，方式为非叶子节点的值 $=$ 两个儿子的值通过该节点运算符计算得到的值。

至于如何建：维护一个 $m a t c h$ 形如： $m a t c h [左括号位置] = 匹配的右括号位置$ ,然后每次判断 $m a t c h [区间左端点 + 1]$ 是否为空，如果不为空说明有对应右括号，此时后面一定有一个运算符，此符号顺序靠后。否则说明当前左端点 + 1指向一个变量，那么 + 2就是一个运算符，顺序靠前，递归下去即可

设 $g_{x, 0 / 1}$ 表示当前节点的值为 $0 / 1$ 的概率，那么根据当前节点符号讨论即可。叶子节点初始化为 $i n v 2$

设 $d p_{x}$ 表示答案，那么对于按位与，只有在 $& 1$ 时当前节点的值才会有影响，所以更新 $d p_{l s}$ 时只需要乘 $g$ 或相反，异或无所谓， $d f s$ 一遍，将路径上的 $g$ 乘起来即为答案

code

T4

其中“类似快速幂”指的是： $m$ 次交换可以视作 $m$ 条形如 $a_{i} - 1 \to a_{i}$ 的边，那么就可以在 $a n s$ 和 $b a s e$ ， $b a s e$ 和 $b a s e$ 之间拼边，有点像图论矩阵

code

2024.11.11

T1 王国边缘

以为是上次的旅行者，直接打了个ksm，然后跑大样例有点慢才意识到复杂度不对... ~~经验主义害人不浅~~

改成倍增就好了， $p_{i, j}, d_{i, j}$ 分别表示跳相应次数的距离在模 $n$ ,模 $m o d$ 下的值，前者算位置，后者算答案

code

T2 买东西题

贪半天出不来，似了

考虑一个物品怎么买下：

折扣价，贡献 $b_{i}$
用优惠券，贡献 $a_{i} - v_{i}$
“抢”之前某物品的券，贡献 $a_{i} - v_{j} - (a_{j} - v_{j}) + b_{j} = a_{i} - (a_{j} - b_{j})$ （学名反悔贪心）

相当于每用一张券，都生成了一张 $v^{'} i = a_{i} - b_{i}$ 的新券，使用它即可表示第三种情况

那么让优先队列在维护当前能用的券的同时多维护一个 $c = a - b$ 即可

code

T3 IMAWANOKIWA

~~太有品，标题也很应景（写作日语译为“弥留之际”...）~~

$n \leq 10$ ：褒叟
序列中没有 $0$ ，此时怎么弄结果都一样，直接每次从 $1$ 开始搞
判断答案：

$n \leq 3000$ ：贪心从头开始改，如果值变了就撤销，否则继续操作。有结论是每次操作位置不超过 $3$ ，所以是平方级别的

综合上述有

61

if(no0)
{
	minn = s[1] - '0';
	hsh = 0;
	for(int i = 2;i <= n;i++)
	{
		minn = __builtin_popcount(minn + (s[i] - '0'));
		hsh = hsh * P + 1;
	}
	cout << minn << " " << hsh << endl; 
	continue;
}
if(n <= 3000)
{
	int res = getans(s,1,n);
	int L = 1;
	while(L < n)
	{
		for(int i = L,num = 1;i <= n;i++,num++)
		{
			cout << "i: " << i << endl;
//			cout << 114 << endl; 
			char s1 = s[i],s2 = s[i + 1];
			int p1 = s[i] - '0',p2 = s[i + 1] - '0';
			p1 = __builtin_popcount(p1 + p2);
			s[i + 1] = p1 + '0';
			for(int j = i;j > L;j--) swap(s[j],s[j - 1]);
			if(getans(s,L + 1,n) == res)
			{
//				cout << 114514 << endl; 
				hsh = hsh * P + num;
				L++;
				break;
			}
			else 
			{
				for(int j = L;j < i;j++) swap(s[j],s[j + 1]);
				s[i + 1] = s2;
			}
//			cout << "L: " << L << endl;
		}
	}
	cout << res << " " << hsh << endl;
	continue;
}
int fi = getans(s,1,n);
cout << fi << " " << 114514 << endl;

std:

分析判断答案中的三种情况发现全是 $0$ 以及只有一个 $2, 0, 2$ 的时候每次从 $1$ 搞就行，所以只需考虑结果为 $1$ 的情况

考虑维护 $1, 2$ 和 $2, 0, 2$ 三种子序列，暴力修改前三位，通过维护三种序列实现均摊 $O (1)$ 的修改，时间复杂度 $O (T n)$

code

2024.11.12

T1 送信卒

~~$min$ 改 $max$ 直接 $10 \to 100$ .......~~

想了一下发现是因为取最小的话会使得 $k$ 较大的可能最短路变成实际选择的路，然后就不符合条件了。。。

code

T2 共轭树图

暴力的 $s u b t a s k$ 就错了一个直接爆死

code

T3 摸鱼军训

记 $r e v_{x}$ 表示 $x$ 前面比 $x$ 大的数的数量，那么 $r e v_{x} \geq k$ 时答案就是 $p o s_{x} - k$ ，还有一种特盘就是 $k \geq n - x + 1$ 时 $x$ 就在 $x$ 处，接下来考虑剩余情况

有一个神秘的结论：对于 $x$ ，他的最终位置是 在原序列中从左往右数第 $k$ 个比 $x$ 大的数的位置 $- k$

南泵。看大佬主食

code

T4 神奇园艺师

50分代码

其中注意到的内容是某某卷积，但抛开那个从组合意义上理解也不难（就是分成独立两部分分别去选，组合+乘法）

代码。。。来不及谢了

2024.11.13

$100 + 15 + 45 + 15$ ，没有挂分，还行

T1 花鳥風月

每个格子变糟只会影响其前驱非法格和后缀非法格形成的区间，用 $s e t$ 维护计算即可，注意去重

code

T2 九莲宝灯

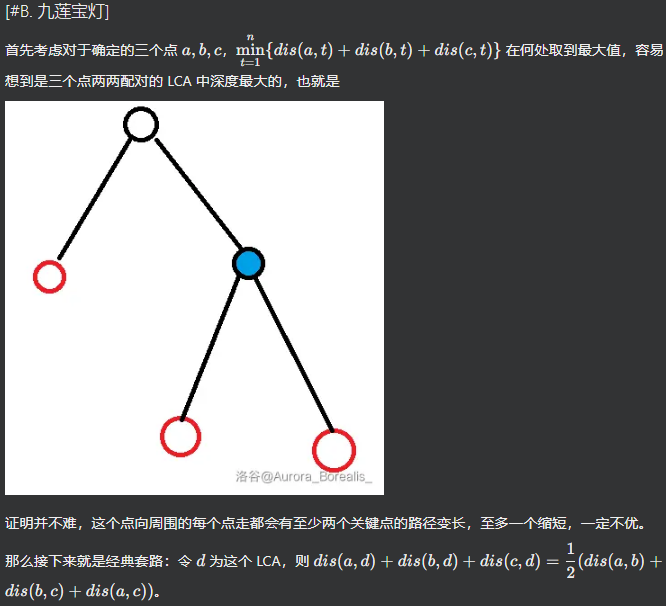
~~容易想到 = 我想不到~~

接上图，那么题目所求即为：

\frac{1}{2} (| C | \times \sum_{i \in A} \sum_{j \in B} d i s (i, j) + | B | \times \sum_{i \in A} \sum_{k \in C} d i s (i, k) + | A | \times \sum_{j \in B} \sum_{k \in C} d i s (j, k))

然后先预处理出每个子树内各集合点的个数，再 $d f s$ 一边根据边统计贡献

code

T3 石上三年

这题部分分中 $k = 1$ 最不好打，首先只有起终点和障碍共线并且障碍在中间才可能绕一下，但是还有可能 只有一行/列，这时直接 $- 1$ 结束

点击查看代码

``` if(k == 1) { if(sx == ex && sx == ob[1].x) { if(min(sy,ey) > ob[1].y || max(sy,ey) < ob[1].y) printf("%d\n",abs(sy - ey)); else { if(n == 1) printf("-1\n"); else printf("%d\n",abs(sy - ey) + 2); } continue; } if(sy == ey && sy == ob[1].y) { if(min(sx,ex) > ob[1].x || max(sx,ex) < ob[1].x) printf("%d\n",abs(sx - ex)); else { if(m == 1) printf("-1\n"); else printf("%d\n",abs(sx - ex) + 2); } continue; } printf("%d\n",abs(sx - ex) + abs(sy - ey)); continue; } ```

正解怎么说呢：如果起终点形成的矩形里没障碍就是曼哈顿距离（这个显然），否则存在一条最短路 贴着障碍走（。。。）

所以预处理障碍四周最多 $120$ 个点到其他点的距离，枚举经过了哪个点来求答案

Tips1: 防止 $M L E :$ 减少 $r e s i z e$ 次数
Tips2: 防止 $T L E :$ 减少数组维数： $d_{i, j, x, y} \to d_{t o t, x, y}$

code

T4 東北新幹線

。。。

60的大炮

dp[0][0] = 0;
for(int i = 1;i < M;i++) dp[0][i] = inf;
while(n--)
{
	scanf("%s",s + 1);
	if(s[1] == 'A')
	{
		int a,b;
		scanf("%d%d",&a,&b);
		cnt++;
		for(int i = 0;i < M;i++) dp[cnt][i] = min(dp[cnt - 1][i] + b,dp[cnt - 1][i ^ a]);
		printf("%d\n",dp[cnt][0]); 
	}
	else
	{
		cnt--;
		printf("%d\n",dp[cnt][0]);
	}
}

code

2024.11.14

菜死了

T1 邻间的骰子之舞

然后少写个+1硬控俩小时。。。

code

T2 星海浮沉录

维护方式和昨天T1类似，找前驱后继，删掉原来的加上新的

code

T4 第八交响曲

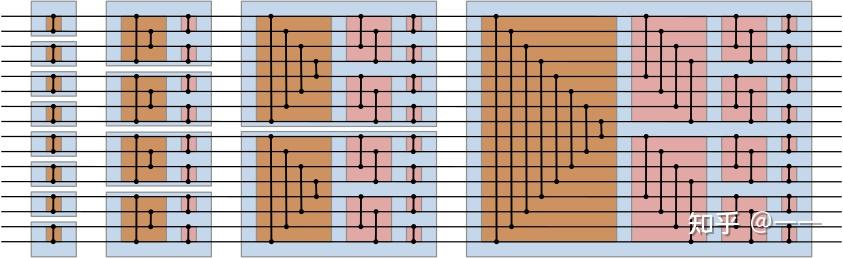
是个叫双调排序的东西，能在 $\log^{2}$ 的复杂度内完成排序

它有两种实现方式，其中一种方向性较强，不适用于这题的一刀切，所以给出另一种方式的实现图解以及代码（代码函数名与图中的颜色对应）

更多也可以看这篇

code

T3 勾指起誓

2024.11.16

原题不会，贪心报废，似了

题面从比赛获得

T1 字符串构造机

10.3考试 $T 1$ ，连边，并查集维护，每次填 $m e x$

code

T2 忍者小队

666开贵了

code

T3 狗卡

贪爆了。。。

code

T4 怪盗德基

臭搜索

2024.11.17

中午不睡，下午崩溃

题面由比赛获得

T1 暴力操作（opt）

除了二分答案其他都想到了。。。

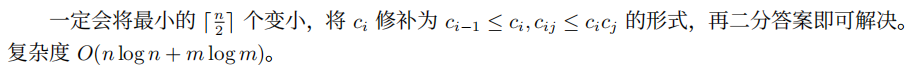
check的话就是算出最小的除数，然后预处理一个后缀 $min$ 即可。

然后会出几个“读取到1，应为0”，说明削成0的代价还有更低的，所以码子里后缀处理到了 $m + 1$

code

T2 异或连通（xor）

忘了加 $m a p$ 记忆化痛失 $30$

勾十题解

首先线段树分治是一种在一些边只在满足一定条件时存在的情况下离线维护图连通性的算法，在时间轴上建立线段树，然后把每条边插入存在区间在线段树上的节点，然后查询时使用并查集搞连通，回溯时撤销。

然后这道题时间轴就是询问（实际上是对 $x$ 排序后的询问时间轴，所以还有映射），通过字典树处理出每个 $x$ 每一位所对应的询问区间，每次插边时在trie树上跑一遍找到其在哪些询问区间存在并插入，最后一把query出来即可

具体的，检查 $K$ 的每一位，如果 $K$ 当前位是 $1$ ，那么 $c_{i}$ 将会在当前节点对应的区间存在（前提是该节点存在），然后跳到异或方向；否则要继续往下比对

code

T3 诡异键盘

T4 民主投票

首先一个点最多可得票数是子树 $s i z e - 1$ ，那么只需要最小化其他点得到票数的最大值即可，这个可以二分+dp

具体的，二分最大值，设 $d p_{x}$ 表示在限制下 $x$ 节点（包括其子树）要向祖先投的票数，形象点就是 $x$ 达到最值后“溢出”的票，如果 $d p_{1} = 0$ 说明可以均摊，二分的值成立

设最终得到的值为 $l i m$ ，那么 $s i z e - 1$ 大于或小于 $l i m$ 的点就直接决定胜负了，接下来考虑等于 $l i m$ 的点，设为 $u_{1}, u_{2} . . .$

如果 $u_{i}$ 只有一个，那么他一定能赢。如果有多个，那么此时的解决办法是以 $l i m - 1$ 为阈值再跑一次上面的 $d p$ ，如果 $d p_{1}$ 不为 $0$ ，那么说明有一个点溢出，并且一直溢到根，那么只要沿着根下去找到这个点即可

code

2024.11.18

T1 草莓

简单的贪心，把 $x, y$ 放一起从大到小排序然后挨个取即可

code

T2 三色

点击查看tj

还得吸个臭氧。。。

code

T3 博弈

至于这个结论，手完几种情况可以发现当差的最低位1是偶数位时不是先手拿下最优情况，就是后手把数列变成三个不同的数使得先手赢，可以参考下面两个例子（第一列 $M, B$ 分别表示先/后手操作完时序列的样子）

[\begin{matrix} a & a & a + 8 \\ M & a & a + 4 & a + 4 \\ B & a + 2 & a + 2 & a + 4 \\ M_{(w i n)} & a + 2 & a + 3 & a + 3 \end{matrix}] [\begin{matrix} a & a & a + 6 \\ M & a & a + 3 & a + 3 \\ B_{(l o s e)} & a + 1 & a + 2 & a + 3 \end{matrix}]

然后祭出字典树，不同的是从低位往高位建树，这样 $d f s$ 时就相当于默认遍历过的位相同，这样减完就都是 $0$ 。然后如果当前深度为奇数，说明下一个分叉就在偶数位上，就要计算一个为 $0$ ，一个为 $1$ 。考虑到只关心最低位，高位怎么样不管，所以要让每个被计算的分叉点的值为其子树的总值，因此要提前遍历一遍，有点像求树的 $s i z e$

~~为什么卡常cnm~~

$80$ 分，就三个过不去

T4 后缀数组

不会平衡树。。。

2024.11.19

T1忘了建树，剩的说实话都不是很会

2024.11.21

T1 图

死都想不到 $p o p c o u n t$ 怎么用，结果一看全是 $b i t s e t$ 。。。事后发现确实好用。。。

就是钦定 $x < y$ ，倒着扫，分开记录 $1, 2, 3$ 的点，然后对于当前点，异或以下能形成边的点集即可

code

T2 序列

不应该往增量去想的。。。

考虑合并 $1, 2$ 操作，即如果 $y > a_{x}$ 时转化为 $+ (y - a_{x})$ ，然后又因为结果是 $\prod$ 形式，所以再全部合并为乘法，就是 $\frac{a_{x}^{'} + y}{a_{x}^{'}}$ ，这里因为实际上的加法是会改变 $a_{x}$ 的，所以要实时更新

最后从大到小排个序挨个去就行了。。。

注：可能有一些劣的操作，所以加入一些 $\frac{1}{1}$ 将其挤到后面，顺便补齐（有些不好的 $1$ 操作会被扔掉导致总数减少）

code

T4 字符串

考虑什么时候多加一个 $t$ ，就是某字符在 $t$ 的位置比前一个字符的位置靠前（或者相等），因此我们考虑维护相邻两个字符所形成的 $n - 1$ 个点对，然后每次查询就看满足 $p o s_{y} \leq p o s_{x}$ 的 $(x, y)$ 有多少了，其中 $p o s_{i}$ 表示字符 $i$ 在 $t$ 中的位置

至于维护，使用线段树。考虑到边界点对只有 $x$ 或 $y$ 会发生变化，所以要分开修改

同时要注意不能越界

modify(max(l - 1,1),r - 1,1,n - 1,1,0,c);
modify(l,min(r,n - 1),1,n - 1,1,c,0);

code

T3 树

什么时候轮流移动 = 走一步了？

看到题后怎么想都是先手一把拉到叶子直接宣告对手的死亡，后手别玩了直接重开吧

结果阳历告诉我1,2,一连先手就输了？神tm为啥？连12先手不高兴了？还是先手大发慈悲打算给后手一点机会？@#￥%@#￥%@#？

然后难受半天跳了

事后得知输出所有情况有90

md整的我跟个sjbrz一样

2024.11.22

T1 镜的绮想

~~STL还是一如既往的辣鸡~~

既然不能用stl，就要把负数转成正的（ $+ 10^{6}$ ），然后不除2，用桶就行

code

T2 万物有灵

想的差不多了，就差加个分桃和等比数列求和了。。。

手玩发现从最后一行选，隔一行选一行就行，然后有周期性，但是 $k$ 是奇数的时候要选的行映射到 $k$ 行内后非常的混乱，只有偶数时是整齐的，所以给奇数加倍。系数和是等比数列，在禁止逆元的情况下有两种写法

类比快速幂法

点击查看代码

ll cal(ll base,ll ci)
{
	ll res = 1;
	ll tot = 1,ba = base;
	ll num = 0;
	while(ci)
	{
		if(ci & 1)
		{
			res = (res + base * qp(ba,num) % mod) % mod;
			num += tot;
		}
		base = base * (1 + qp(ba,tot)) % mod;
		tot *= 2;
		ci >>= 1;
	}
	return res;
}

递归法

注意这个东西计算的是

S + S^{2} + . . .

（由图可知），是没有

+ 1

的

ll cal(ll base,ll ci)
{
	if(!ci) return 1;
	if(ci == 1) return base;
	ll res = 0;
	if(ci & 1) res = (qp(base,ci) + (1 + qp(base,ci / 2)) % mod * cal(base,ci / 2) % mod) % mod;
	else res = (1 + qp(base,ci / 2)) % mod * cal(base,ci / 2) % mod;
	return res;
}

T3 白石溪

~~大炮怎么还挂了两个点~~

假设全是蓝色，现在要往里放红的，那么每个红石头的贡献 $W_{i}$ 就是 $a_{i} - b_{i} + c (i - 1) + d (n - i)$ ，但这是只有一个红石头的情况，如果有 $x$ 个，那么 $c ， d$ 就会多算。具体的，每两个红石头，靠前的一个会使得靠后的一个的贡献少一个 $d$ ，类似的，后面的会使前面的少一个 $c$ ，所以要减去 $(c + d) C_{x}^{2}$

然后发现减去的只与个数有关，所以枚举个数，按 $W$ 贪心选即可

code

T4 上山岗

先说部分分：

首先算出最多能登几座山，然后对于每座山，在剩下的人中二分答案，注意字典序最大时当前山可能登不上去，所以要分成 $\leq a_{i}$ 和 $> a_{i}$ 两部分二分，使用 $m u l t i s e t$ 暴力维护

code

然后发现这匹配模式有点像田忌赛马（？），所以先将能力值排序，从小到大枚举每一个登山队员找到最靠右的合法匹配位置，这样构造下来字典序是较小的，并且匹配数是最多的。

然后考虑在保证匹配数最多的情况下移动。贪心地，按能力值从大到小枚举队员。如果该队员当前有匹配的位置，那么找到最左端的未匹配的位置来置换，这样的位置是确定下来的；如果没有匹配的位置，那就随便找到一个最靠左没有被确定的位置，如果这个位置被其他人匹配过了，那就强制把那个人拆下来，把现在这个人换上去。因为比他小的人都有匹配，那这个人一定也有匹配。由于从大到小确定位置构造，这样的字典序一定最大。

code

2024.11.23

每次在MX上考试都感觉脑子灌了shit

T1 排序

字典树，然后不会了

事后发现没必要，直接扫一遍看有哪些数位要放 $1$ ，有矛盾就是无解，每次修改时删掉旧贡献加上新贡献就行。。。

code

T2 交换

置换和倍增都写成型了，周期除成 $n$ 了。。。也没想到左移的方法

code

剩的有点不太会呀。。。

2024.11.25

以为是四道T4，但事后发现并没有想象的那么难，以后还是不要预设难度了，就题论题

比赛链接

T1

错误认为是大炮，结果是个贪。。。

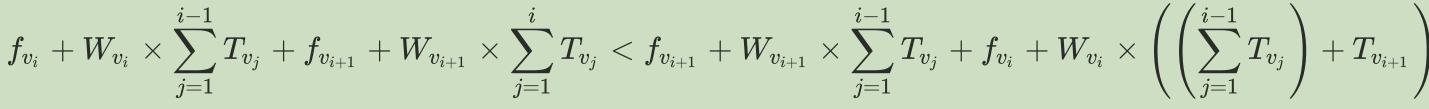
化简：

W_{v_{i + 1}} T_{v_{i}} < W_{v_{i}} T_{v_{i + 1}}

code

T2

先求 $d f n$ 序，那么一个子树就可以视作一个区间。对于一个人 $x$ ，把和他有相同奖励的人（包括自己）的子树扔到线段树上，答案就是覆盖的点数。遍历树，进这个点时加区间，出这个点时删掉，每次查询全局数量即可

注意如果 $a, b$ 存在祖先关系，只考虑祖先

code

T3

有一点要注意的是原始的差分数组下标从 $0$ 开始，要强制平移然后再求前缀和

code

T4

核心意思就是我们可以证明序列 $S$ 和设的 $t$ 一定条件下存在一一对应关系，只要 $t$ 满足条件，就可以直接对 $t$ 计数而做到不重不漏

code

然而我是大常熟选手。。。

60ptsTLE马

2024.11.26

是落谷比赛

T1 打印

用线段树维护每个打印机的等待时间，每次有新文件时先减掉与上一个文件的时差，然后二分找合适的就行

code

T2 飞船

以为是实数二分答案，没救了

定义 $d p_{i, j}$ 为到达第 $i$ 个加油站，速度为 $j$ 时的方案数，又因为 $x \in 1, 2, 3, 4$ ，所以 $j = 2^{p} 3^{q}$ ，所以修改 $d p$ 为 $d p_{i, p, q}$ 表示速度为 $2^{p} 3^{q}$ 时的最短代价。以加 $2$ 号油为例，转移就是

d p_{i, p, q} = min (d p_{i - 1, p, q} + \frac{d i s}{2^{p} 3^{q}}, d p_{i - 1, p - 1, q} + \frac{d i s}{2^{p - 1} 3^{q}} + t_{i})

其他类似

由于开的浮点，内存比较卡，可以滚动优化，不过此时就要边大炮边计算，否则答案就滚掉了。具体就是在计算 $d p$ 时先把在当前点与上一个点之间的 $y$ 算掉，用上一个点的大炮值

有一个细节是每个油只能加一次，所以倒序枚举

code

T3 简单的字符串问题2

这里求 $g_{l, 1}$ 使用二分+哈希优化， $R M Q$ 线段树也不是不行(doge)

意思就是每个 $g_{l, k}$ 会给一个区间加上一个等差数列（递减的），考虑使用二阶差分维护

考虑如何修改，下面是个例子（设首项为 $a$ ，公差是 $d$ ,修改 $[3, 6]$ ）

原数列(其二阶差分中从第三项开始都是 $0$ )	1	2	3	4	5	6	7	8	9
操作后	1	2	3 + $a$	$4 + a + d$	$5 + a + 2 d$	$6 + a + 3 d$	7	8	9
一阶差分 $Δ d$	1	1	$a + 1$	$d + 1$	$d + 1$	$d + 1$	$1 - a - 3 d$	1	1
二阶差分 $Δ^{2} d$	1	0	$a$	$d - a$	$0$	$0$	$- a - 4 d$	$a + 3 d$	0

会发现修改了四个值，即

Δ^{2} d_{l} + = a

Δ^{2} d_{l + 1} + = d - a

Δ^{2} d_{r + 1} - = a + d (r - l + 1)

Δ^{2} d_{r + 2} + = a + d (r - l)

类比使用即可

70ptscode（由于数据范围不同，数组要换，所以马较长，其实核心看一个 $i f$ 就够了）

92pts参考

T4 咕咕咕

2024.11.27

T1 排水系统

按题模拟即可，要注意的是结果约分以及以int128格式输出

code

T2 三元组

以为是数论，然而不是。。。

对于一个 $b$ ， $a + b^{2}$ 的范围是 $[1 + b^{2}, b + b^{2}]$ ，然后将区间用取模映射到 $[0, k - 1]$ 中，但此时原区间长度横跨多个 $[0, k - 1]$ ，还会出现左端点跑到右端点右边的情况，分讨区间加，然后再把枚举的 $b$ 当 $c$ （此时树状数组里都是 $\leq i$ 数的答案），查询一下 $c^{3} m o d k$ 对应的点的值就行了

code

T3 微信步数

~~最近的紫色都太有实力了~~

首先进行一个转化：我们让 $P$ 个起点同时开始走，对于每一步，统计能走这一步的点数，总和就是答案

下称走一个 $n$ 步为一轮，出界的点为“废弃”

先考虑一个维度 $j$ 。

一轮过后，剩下的点会是连续的一段区间，设长度为 $l e n_{j}$ ，那么贡献就是 $\prod_{j = 1}^{k} l e n$

设一轮中走到第 $i$ 步最多向左走 $l_{i}$ 步，向右走 $r_{i}$ 步（更直白的是该维度上 $d$ 的前缀和的最大最小值），那么剩下的点数就是 $v a l_{1_{j}} = w_{j} - (- l_{i} + r_{i})$ ，由于 $d$ 的前缀和可能是负数，所以 $l_{j}$ 可能是负的（也可以理解为钦定向右为正方向）

设第一轮总偏移量为 $b u_{j}$ ，那么以第一轮的位移为边界，可以得到第二轮第 $i$ 步时左右位移增量 $l_{i}^{'}, r_{i}^{'}$

第一维：步数，第二维：维度

for(int i = 1;i <= n;i++) 
	for(int j = 1;j <= k;j++)
	{
		r[i][j] = max(0,r[i][j] + bu[j] - r[n][j]);
		l[i][j] = min(0,l[i][j] + bu[j] - l[n][j]);
	}

那么每一步新废弃的点就是 $f_{i} = r_{i}^{'} - l_{i}^{'}$ ，一轮下来该维度总共废弃 $v a l_{2_{j}} = r_{n} - l_{n}$

暴力枚举轮数的复杂度是玄学的，考虑有无规律

此时手玩会有下面的结论：第 $2, 3, 4, 5. . .$ 轮每一步废弃的点是一样的，只有第一轮特殊

例子：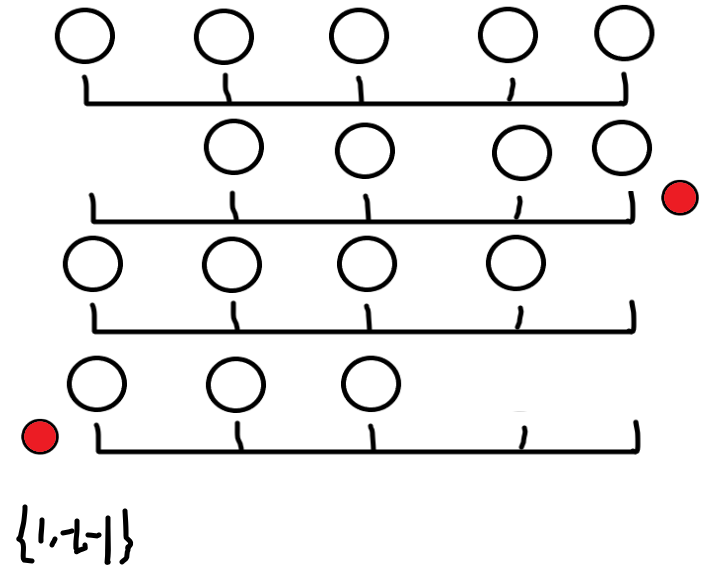

图示为执行左下角指令一轮后的形式，可以发现第一轮中左右各损失一个点，然后可以发现从第二轮开始剩下的点只可能在走完第三步后从左边被废弃，即除了第一轮，剩下的废弃模式就是一样的

每一维度都一样，开始求答案

设当前完整走了 $x$ 轮（不含第一轮），则 $x \leq {min}_{j = 1}^{k} \frac{v a l_{1_{j}} - f_{i}}{v a l_{2_{j}}}$ ，就是当有一个维度全部报废时停止计算

那么走到第 $x + 2$ 轮的第 $i$ 步时，第 $j$ 维还剩下 $v a l_{1_{j}} + (- v a l_{2_{j}}) x - f_{i}$ 个点，那么贡献就是 $\prod_{j = 1}^{k} (v a l_{1_{j}} + (- v a l_{2_{j}}) x - f_{i})$

本来是枚举 $i, x$ 计算，但是我们发现求的东西形如 $\sum_{i = 1}^{n} \sum_{x = 0}^{T} \prod_{j = 1}^{k} [(- v a l_{2_{j}}) x + P]$ ，连乘形如 $F (x) = \sum p_{i} x^{i}$ ，所以第二个求和可以得到各项系数后使用拉碴计算

接下来计算系数，可以使用大炮

定义当前处理了连乘中的 $j$ 项， $x^{k}$ 的系数为 $x i_{j, k}$ ，每次新乘进去的都是 $(- v a l_{2, j}) x + P$ ，其中常数项不会改变次数，从 $x i_{j - 1, k}$ 转移，含 $x$ 项会使得系数升高 $1$ ，从 $x i_{j - 1, k - 1}$ 转移

点击查看代码

for(int j = 1;j <= k;j++)
{
	int x = val1[j] - (r[i][j] - l[i][j]);
//	cout << "x: " << x << endl;
	if(x <= 0) goto nxt;//一个维度爆炸了直接停 
	if(val2[j] > 0) t = min(t,x / val2[j]);
    for(int p = 0;p <= k;p++)
	{
		xi[j][p] = xi[j - 1][p] * x % mod;
		if(p > 0) xi[j][p] = (xi[j][p] + xi[j - 1][p - 1] * (-val2[j]) % mod) % mod;
	}
}

那么 $\sum_{x = 0}^{T} F (x) = \sum x i_{k, j} \sum_{x = 0}^{T} x^{j}$ ，拉擦搞搞就行

code

T4移球游戏

超超超超吊的大构造

这边建议直接去看题解，太屌了

2024.11.28 NOIP终结篇

~~标题党，为了观感不放题目名了~~

T1

手玩发现每次的贡献都是两两相乘的结果，那就算出贡献，再乘以方案数即可。而方案数也不难，就是 $\prod_{i = 2}^{n} C_{n}^{2}$

code

T2

策略死了

可行的一种策略有点像赛道修建，每次先把儿子匹配，有剩的就往上配，只不过这里的树是搜索树，不能走返祖边

code

T3

发现答案等于 $2 + 满足题目要求的 i 的个数$ ，所以不用关心序列内容，只需维护前后端，每次区间加的时候合并序列并检查有没有端点成为答案。由于涉及三个值，所以前后两个值要维护，就要特判长度为 $0, 1$ 的情况

注意只有当序列长大于 $2$ 的时候才统计 $i$ 的个数

code

T4

下称两点间距离为每一维度上距离的最大值， $a$ 的另一半是 $b$ ， $b$ 的另一半是 $a$

二分，然后发现形式同 $2 - S A T$ ，用这个去 $c h e c k$

具体的，首先每个点对的 $(a, b)$ 存在一个去，另一个不去的关系，然后对于所有的 $a, b$ ，两两之间存在一个取的到时另一个取不到的情况（如果二分值不够两点距离的话），然后建图跑 $t a r j a n$ 检验

但是上面的方法是 $n^{2}$ 级别的，加个维度什么的空间吃不消，考虑优化

发现所有 $a, b$ 的逻辑可以细化为： $a$ 的一个维度取不到， $b$ 的所有维度都要取到，或者说取了一个点，其所有维度都取到了；有一个维度取不到，这个点就取不到。那么枚举维度，枚举点，先把边长压到当前点上表示选择当前点维度，然后排序+双指针将此时该维度取不到的坐标扫出来，那么这些坐标对应的点就取不到。既然这些点取不到，那么另一半要取到，所以先把要取到的点连成一坨，然后把当前点连进去就好了。又因为左右端点都可以压（这是小性质：边长端点压坐标上较优），所以正序倒序各跑一遍

sort还用了神秘小科技，表示所有点按当前维度排序

for(int i = 1;i <= k;i++)
{
	sort(a + 1,a + 2 * n + 1,[&](node p,node q) {return p.x[i] < q.x[i];});
	int pre = ++all;
	int l = 1,r = 1;
	while(r <= 2 * n)
	{
		while(a[r].x[i] - a[l].x[i] > lim) 
		{
			all++; add(all,pre);
			pre = all; add(pre,inv(a[l].id));
			l++;
		}
		if(l != 1) add(a[r].id,pre);
		r++;
	}
	int suf = ++ all;
	l = r = 2 * n;
	while(l >= 1)
	{
		while(a[r].x[i] - a[l].x[i] > lim) 
		{
			all++; add(all,suf);
			suf = all; add(suf,inv(a[r].id));
			r--;
		}
		if(r != 2 * n) add(a[l].id,suf);
		l--;
	}
}

posted @ 2024-11-13 20:30 why?123 阅读(16) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 模拟赛总结(二)

· 模拟赛总结（三）

· 模拟赛总结

· 多校A层冲刺NOIP2024模拟赛19

· NOI 2024 前做题纪要

阅读排行：
· 地球OL攻略 —— 某应届生求职总结
· 周边上新：园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源！
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】

公告

昵称： why?123
园龄： 1年
粉丝： 4
关注： 2

+加关注

2025年3月

日

一

二

三

四

五

六

2024.10.30

T1 追逐游戏 (chase)

T2 统计

T3 软件工程

T4 命运的X

2024.10.31

T1 四舍五入

T2 填算符

T3 道路修建

T4 逆序图

2024.11.1

T1 网格

T2 矩形

T3 集合

T4 倒水

2024.11.2

T1 Median

T2 Game

T3 Park

T4 路径

2024.11.4

T1 赌神

T2 幸运数字

T3 建筑师

T4 大写锁定

2024.11.5

T1 选彩笔（rgb

T2 兵蚁排序（sort）

T3 人口局 DBA（dba）

T4 银行的源起（banking）

2024.11.6

T1 新的阶乘

T2 博弈树

T3 划分

T4 灯笼

2024.11.7

T1 图书管理

T2 两棵树

T3 函数（fun）

T4 编辑

30pts

100pts

2024.11.10

T1

T2

T3

T4

2024.11.11

T1 王国边缘

T2 买东西题

T3 IMAWANOKIWA

2024.11.12

T1 送信卒

T2 共轭树图

T3 摸鱼军训

T4 神奇园艺师

2024.11.13

T1 花鳥風月

T2 九莲宝灯

T3 石上三年

T4 東北新幹線

2024.11.14

T1 邻间的骰子之舞

T2 星海浮沉录

T4 第八交响曲

T3 勾指起誓

2024.11.16

T1 字符串构造机

T2 忍者小队

T3 狗卡

T4 怪盗德基

2024.11.17

T1 暴力操作（opt）

T2 异或连通（xor）

T3 诡异键盘

T4 民主投票

2024.11.18

T1 草莓

T2 三色

T3 博弈