专(diao)题大赏
USACO の small Trick杂题
核心Trick使用粗体强调
1.Breakdown P
删改加不多说
考虑\(K\)很小，不妨meet in the middle，此时\(k = 4\)
处理出只包含一条边，两条边的“小组件”去“拼出”最短路，每次加边只需要更新新边端点涉及的组件以及最短路即可
2.Making Friends P
扫一遍，每个点向比他大的点建关系，然后合并
可以用\(set\)，也可以使用线段树合并
3.Palindromes P
考虑每一对字母移到某区间对称位置的贡献，位置\(l,r\)，区间\([L,r]\)，贡献\(|l + r - L - R|\)
分奇偶性讨论，每次由内向外从一对扩展到另一对，使用树状数组维护\(l + r\),\(L + R\)
4.Tractor Paths P
倍增
预处理出每个区间向左/右跳\(2^i\)步最远能跳到哪个区间，这个可以求出第一问
对于第二问，考虑前缀和，沿用上面的倍增，求出\(2^i\)步内有多少个特殊区间，最后使用右-左即为答案
5.Mana Collection P
推式子
设确定要收集的点集为\({c_k}\)，对应到达时刻为\({t_k}\)那么有式子\(ans = \sum\limits_{i = 1}^k m_{c_k}\times t_k\)
考虑时间拉满肯定不劣，所以\(t_i = s - \sum\limits_{j = i}^{k - 1}d(c_j,c_{j + 1})\)
带入:
之所以把后面变一下，是方便状压预处理
第一维表示选的点集，第二维是终点，\(d\)用\(Floyd\)预处理,\(sum = \sum_{i = 1}^k m_{c_i}\)
然后回到式子，发现可以令\(B = - \sum\limits _{i = 1}^{k - 1}d(c_i,c_{i + 1})\sum\limits_{j = 1}^{i}m_{c_i}\),也就是\(dp_{S,c_k}\)，\(K = \sum_{i = 1}^k m_{c_i}\)，\(x = s\)就是直线，可以上李超树，注意终点不同的要放入不同的树中
动态维护即可，复杂度没问题
Hungry Cow P
利用线段树的merge实现类似平推操作
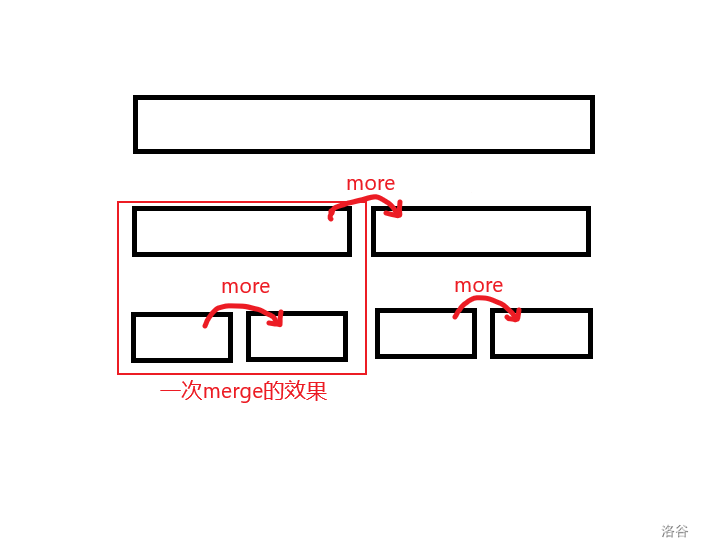
考虑到要把新加的草往右匀，原先有草吃的天跳过，以此计算贡献，使用线段树实现，记录当前区间有草吃天数\(has\)，多出的草\(more\)，答案\(sum\)，以及向后匀的贡献\(giv\)（根据线段树的结构，就是填右子区间的贡献）
理论可匀 $\max(mor - [(r - mid) - has],0) $,最多 \(r - mid\)，二者比大小实现草的剩余等量的转移
考虑到1e14的威压一定要多取模还要考虑线段树大小以及维护的区间的大小
Subtree Activation P
搞出优秀路径及其性质后跑大炮
定义一个点被标记为某时刻该点满足了条件1，将点按照标记先后排列到树上形成若干路径
根据样例和手摸可以猜到优秀路径只可能是下面几种
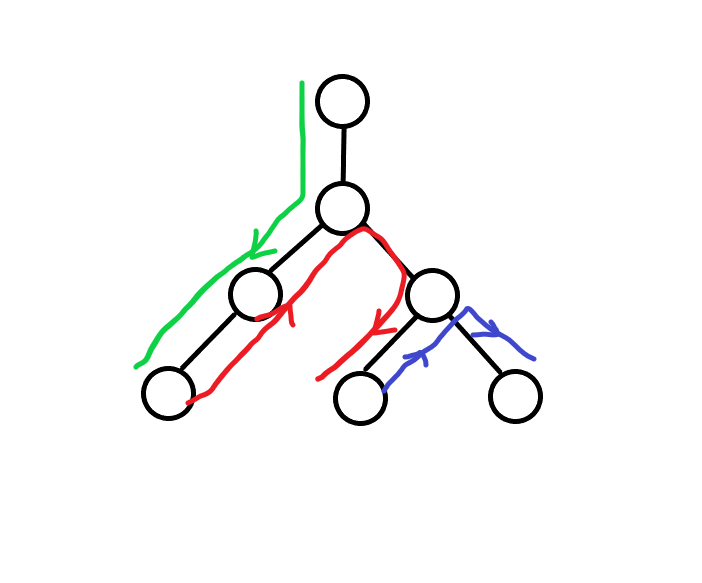
然后接着手玩可以发现标记一条序列上所有点的最小花费是深度最浅的点的\(siz\)的两倍
接着可以想到最优情况下序列互不交叉
然后可以使用树形大炮，用没标记的链结合当前节点拼路径
Problem Setting P
状压出每道题的难易程度，得到\(n\)个\(m\)位的状态，结合题意会发现选择的相邻两道题前者是后者的子集（认为这道题难的下一道仍然难，还有一部分从后一道题开始认为难）
状态相同的可以合并，方案 $ = \sum\limits_{i = 1}^{num} A_{num}^i$
设\(dp_s\)表示最后一道题状态是\(s\)的方案数
枚举当前最后一道题的状态\(S\)，那么前面一共有\(1 + \sum dp_s\)种方案，其中\(s \subseteq S\)，\(+1\)是因为前面可以不选，乘上自己的方案数就是\(dp_S\)
但是实际只有\(60\)，考虑优化
可以沿用\(dp\)的尿性，钦定子集只比全集少一个\(1\)，这样枚举每一位即可，那就预处理\(ret_{s,j}\)表示状态为\(s\)，与全集相比最大的少一处为\(j\)的情况下的\(dp\)总和，也就是说，可能有多位少\(1\)，\(j\)位是编号最大的一位
转移即可
Watching Cowflix P
看牛片
首先\(dp\)，设\(dp_{u,0/1}\)表示节点\(u\)是否属于连通块，然后有
然后可以有\(naive\)的\(n^2\)，考虑优化
使用 惊人的观察力 发现部分答案的差一定而且差单调递减，考虑使用根号分治
\(k < \sqrt n\)时暴力大炮
\(k > \sqrt n\)时二分出所有差变化的位置，然后递推即可
注：卡常，使用\(dfn\)序优化把搜索改成线性遍历
Pareidolia P
使用线段树维护矩阵（？？？）
无修改时有大炮，使用矩阵转移，带修改的话对每一位字符构一个矩阵，使用线段树维护
Good Bitstrings P
真史登场
数形结合
规定射线\((x,y)\)表示从原点出发经过\((x,y)\)的线
定义点\((ia,ib)\)，将变化过程画到平面上，得到从\((0,0)\)到\((a,b)\)的路径
结合判断条件以及图形可得：当前点在射线\((a,b)\)上方时向右走，反之向上走
那么路径上的整点就是所有前缀
考虑合法点\((x,y)\)的性质
1.射线\((a,b)\)和射线\((x,y)\)中间没有路径上的其他点
证明：显然如果有的话会出现不同的决策，矛盾
2.已知合法点\(f_1,f_2\)，如果\(f\)代表的射线在\(f_1,f_2\)中间，且有\(f_1 \times f_2 = 1\)（向量叉积），那么\(f = k_1f_1 + k_2f_2\)
证明：\(f = (f \times f_1)f_2 + (f \times f_2)f_1\)
这样就有\(f = f_1 + f_2\)
然后就有算法，见第一篇题解
简单手膜发现还有一些东西
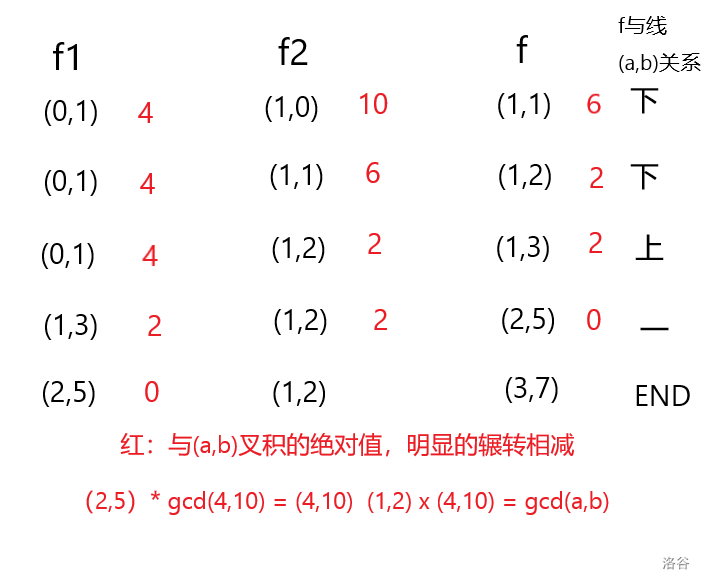
3.结束时\(f_1,f_2\)中有一个满足等于\((\frac{a}{\gcd(a,b)},\frac{b}{\gcd(a,b)})\)，且另一个与\((a,b)\)叉积的值为\(\gcd\)
也就是说整个过程就是个辗转相减，可以转化成辗转相除从而实现\(log\)的复杂度
剩下一些细节见tj
Triples of Cows P
\(deep ♂ dark ♂ fantacy\) 不可做
Paired Up P
大炮
- \(T = 1\)
相对简单，设\(dp_{i,j}\)表示前\(i\)头\(H\),\(j\)头\(G\)完成配对时最大体重和
\(ans = \sum W - dp_{H,G}\)
- \(T = 2\)
考虑直接\(dp\)出答案
定义\(dp_{i,j,k}\)表示前\(i\)头\(H\),\(j\)头\(G\)完成配对，最后一个未配对的牛是\(k\)的最大值
这样转移是三次方的，考虑优化
保留前两维，我们可以使用两个数组分别表示最后一个未配对的牛是\(H\)或是\(G\)，然后可以互相转移，通过提前预处理某区间内极大配对牛数量和一头牛的最小标号配对牛可以实现快速转移
注：这里的区间\(lst_{i,j}\)表示第\(i - numh\),第\(j - numg\)头牛中的极大配对数
HILO
转化成期望
定义\(dp_{i,j,0/1}\)表示还剩下\(i\)个小于\(x\)的有效数字，\(j\)个大于\(x\)的有效数字，前一次喊的是
LO(0)/HI(1)，然后用反向跑的方法去大炮
那么每次选择一个数，都只影响其所在的区域（> / <\(x\)），另一维不影响，考虑到选择后废弃的数字有多种可能，所以要遍历。如果前一次喊的是HI，那么这次如果喊LO期望次数就会增加，增量为\(\frac{i}{i + j}\)
即
使用前缀和优化即可
Minimizing Haybales P
聚聚爆
对于每个数，二分找出他可以换到的位置区间，可以使用线段树维护区间最值实现，然后在活动区间中找到最左边的大于该数的位置，把他扔到那里，那么可能一些位置有多个数，为了字典序最小，使用\(multiset\)维护即可（因为有重复元素）
贪（luan）心（gao）
所有正确的贪心一定有科学的理由
国王游戏
根据直觉按照\(b\)升序排列能得一半分
考虑大臣1和大臣2位置能交换的必要条件是：大臣2放在大臣1的前面得到的最大值更加小。那么讨论两种情况下的最值：
如果大臣1放在前面，他俩获得的金币数分别为：\(\frac{a_0}{b_1},\frac{a_0 \times a_1}{b_2}\)
如果大臣2放在前面，他俩获得的金币数分别为：\(\frac{a_0}{b_2},\frac{a_0 \times a_2}{b_1}\)
约去式子里面的a0，就变成了比较：\(\max(\frac{1}{b_1},\frac{a_1}{b_2})\)和\(\max(\frac{1}{b_2},\frac{a_2}{b_1})\)的大小
根据\(a > 0\)，可得: \(\frac{a_1}{b_2} \geq \frac{1}{b_2}\)、\(\frac{1}{b_1} \leq \frac{a_2}{b_1}\)
那么，如果\(\frac{1}{b_1}\)是最大的，则\(\frac{1}{b_1} \geq \frac{a_2}{b_1}\)，只可能左右两边相等，则有\(\frac{1}{b_2} \leq \frac{a_2}{b_1}\)，所以两种情况的最大值是一样的，则不用交换。同理可得\(\frac{1}{b_2}\)是最大的情况也不用交换。
那么如果\(\frac{a_1}{b_2} > \frac{a_2}{b_1}\)，那么就要交换，变形得：
$$a_1 \times b_1 > a_2 \times b_2$$
表示要交换，我们排序就只要按照\(a \times b\)的从小到大排就可以了。
高精传统美德
皇后游戏
根据直觉认为\(a\)越小越好（减少大值的累加），\(b\)越大越好（在\(\sum a\)还小的时候加入大值），两种情况分别跑一遍然后取\(\min\)可得\(70\)...
首先证明直觉有一定正确性
沿用上一道题的方法，考虑相邻两个人的交换条件。由于奖金单调，所以后一个人的一定更大。设大臣\(i\)后面的大臣为\(j\)，\(i\)前面的\(\sum a\)为\(x\)，\(i\)前面一位大臣奖金为\(y\),则
化简为：\(\max(y + b_i + b_j,x + a_j + b_i + b_j,x + a_i + a_j + b_i)\)
同理可得交换后\(i\)的奖金
那么不交换更优，那么
其中\(y + b_i + b_j\)没有本质上的影响，直接消掉。类似的，\(x\)也能消掉：
然后提出相同的，移项
较大数会被减掉，留下较小数的相反数，变个号得到
分讨：
-
\(a_i < b_i\),\(a_j < b_j\)时，\(a_i \leq a_j\)，按照\(a\)升序
-
都相等：无所谓
-
\(a_i > b_i\),\(a_j > b_j\)时，\(b_i \geq b_j\)，按照\(b\)降序
所以猜想是有合理性的，重点在于\(a,b\)谁的“影响力”更大
所以维护\(a,b\)的大小关系，由此排序
其中$del$只会是$-1,0,1$
bool cmp1(node x,node y)
{
// return min(x.a,y.b) < min(y.b,y.a);
if(x.del == y.del)
{
if(x.del <= 0) return x.a < y.a;
else return x.b > y.b;
}
return x.del < y.del;
}
加法
首先二分答案，考虑用贪心搞\(check\)
那么为了最大化效果，肯定选当前可选区间中右端点最大的，所以使用优先队列维护备选区间，然后遇到需要填的数字时，如果原先有的区间数不够，就从队列里取新的，但是新区间要满足右端点长于当前位置才能使用，扫一遍即可
赛道修建
- \(m = 1\)：直径
点击查看代码
if(m == 1)//直径
{
dfs(1,0); st = pos;
memset(d,0,sizeof(d));
dfs(st,0); ed = pos;
printf("%d\n",d[ed]);
return 0;
}
- \(a_i = 1\): 菊花图，此时赛道最多两条边。最优肯定是两两组合。分讨，如果两两组合能凑够\(m\)条，那肯定是用排序后的边中后\(2m\)条组，大配小即可。否则需要用一些单边当赛道，那么首先要最小化单边数量，然后肯定用最大的边做单边，剩下的大配小
点击查看代码
if(ifjh)//菊花
{
sort(val + 1,val + num + 1);
if(m <= (n - 1) / 2)
{
int pos = n - 1 - m * 2;
int l = pos + 1,r = num;
for(int i = 1;i <= m;i++) pat[++tot] = val[l] + val[r],l++,r--;
sort(pat + 1,pat + tot + 1);
printf("%d\n",pat[1]);
}
else
{
int x = (n - 1 - m); int sig = n - 1 - 2 * x;
int l = 1,r = num - sig;
for(int i = 1;i <= x;i++) pat[++tot] = val[l] + val[r],l++,r--;
for(int i = 2 * x + 1;i <= num;i++) pat[++tot] = val[i];
sort(pat + 1,pat + tot + 1);
printf("%d\n",pat[1]);
}
return 0;
}
- \(b_i = a_i + 1\)：链，二分答案+贪心\(check\)即可，注意\(val\)数组不能排序，是\(dfs\)的遍历顺序
点击查看代码
if(ifchain)//链
{
dfs(1,0); num = 0;
for(int i = 2;i <= n;i++) val[++num] = d[i] - d[i - 1];
int res = 0,L = 1,R = all;
while(L <= R)
{
int mid = L + R >> 1;
if(check(mid)) res = mid,L = mid + 1;
else R = mid - 1;
}
printf("%d\n",res);
return 0;
}
以上一共\(55\)分
std:
首先二分答案
对于每个点，优先将他的儿子之间配对形成赛道，剩下未配对的儿子中挑个最大的传上去（与祖先们形成赛道）
考虑配对方式。如果一个儿子就已经满足二分的值，就不配了直接删。否则找一个最小的与当前儿子加起来能满足二分值的儿子，将二者同时删去，一直配到不能再配为止
由于重复元素，使用\(multiset\)维护
一些特判：
-
如果找到的位置是自己，指针往后跳一位
-
如果当前集合里就剩一个元素，直接比对不配了
点击查看代码
int Dfs(int x,int fa,int lim)
{
s[x].clear();
for(int i = head[x];i;i = e[i].next)
{
int k = e[i].to;
if(k == fa) continue;
int ret = Dfs(k,x,lim) + e[i].w;
if(ret >= lim) sum++;
else s[x].insert(ret);
}
int maxx = 0;
while(!s[x].empty())
{
int tmp = *s[x].begin();//待配对元素
if(s[x].size() == 1) return max(maxx,tmp);
auto pos = s[x].lower_bound(lim - tmp);
if(pos == s[x].begin()) pos++;//找到它自己，往后跳一个
if(pos == s[x].end())//没找见
{
maxx = max(maxx,tmp);
s[x].erase(s[x].begin());
}
else//配对的一起删
{
sum++;
s[x].erase(pos); s[x].erase(s[x].begin());
}
}
return maxx;
}
让我们赢得选举
明显，在\(B_i \neq -1\)时，获得协作者必能得到选票
所以考虑按照\(B\)排序。
然后考虑到有些州\(B\)很大但\(A\)很小，所以用大炮维护
但是大炮有一个问题：
大炮是遍历，然而最优策略其实是先选人再去专心拿票，这就使得走的州的顺序在排序后的数列上可能是跳跃的
怎么办呢？
但有一点是不变的：选人肯定从前若干个选
然后就很骚了：枚举选了多少个人(\(x\))，然后将大炮两维定义为票数和人数，在计入拿票代价时直接除以\(x + 1\)，其他正常
注意第七行
for(int i = 0;i < N;i++) for(int j = 0;j < N;j++) dp[i][j] = 1.0e9;
dp[0][0] = 0;
for(int i = 1;i <= lim;i++)
{
for(int j = 0;j <= x;j++)
{
dp[i][j] = min(dp[i][j],dp[i - 1][j] + sta[i].a * 1.0 / (x + 1));
if(j > 0 && sta[i].b != 1e9) dp[i][j] = min(dp[i][j],dp[i - 1][j - 1] + sta[i].b * 1.0 / j);
}
}
接着，这\(x\)个人能拿的票数\(\in [x,k]\)，那么枚举他们拿的票数\(i\)，此时这里还有一个性质：这\(i\)张票肯定全部来自前\(i\)个州。那么第\(i + 1\)到第\(n\)部分 按照\(A\)贪心 去选剩的\(k - i\)张，然后与大炮合并即可
点击查看代码
db res = 1.0e9;
for(int i = lim;i >= x;i--)//这里要倒序，因为要排序，正向的话会乱
{
sort(a + i + 1,a + n + 1);
int sum = 0;
for(int j = i + 1;j <= lim;j++) sum += a[j];
res = min(res,dp[i][x] + sum * 1.0 / (x + 1));
}
ans = min(ans,res);
双序列拓展
性质题
首先翻译一个东西：\(\forall 1 \le i,j \le l_0\) 都有 \((f_i - g_i)(f_j - g_j) > 0\)。实际上就是\(\forall i \in [1,l_0],f_i > g_i\)或\(f_i < g_i\)
结合这个东西，就能得到拓展的目的：如果当前位的\(Y\)与\(X\)不符合关系，将前面的\(Y/X\)延展过来
那么不妨使用第一项确定一种大小关系去搞，如果不符合就把序列交换一下看行不行
不妨设为\(X< Y\)
那么首先可以有一个大炮\(dp_{i,j}\)表示当前匹配到\(X\)的第\(i\)位，\(Y\)的第\(j\)位是否能扩展，\(dp_{1,1} = 1\),然后当\(X_i < Y_j\)时转移即可
点击查看代码
dp[1][1] = 1;
for(int i = 1;i <= lena;i++)
for(int j = 1;j <= lenb;j++)
if(a[i] < b[j]) dp[i][j] = (dp[i][j] | dp[i][j - 1] | dp[i - 1][j] | dp[i - 1][j - 1]);
然后观察特殊性质，发现提到了最值，提醒我们从这方面考虑
再次注意到题目中有一个条件：\(L\)是一个正整数序列
这个条件比较重要，这说明：\(Y\)中的每一个元素都会与\(X\)中某个元素相对
那么，如果\(Y_{min} \leq X_{min}\)，就说明\(Y_{min}\)这个位置一定不能满足\(X < Y\)的要求，\(Y_{max} \leq X_{max}\)同理，即没有\(Y\)能胜任\(X_{max}\)所在位置
此时我们得到了两个判据，接下来进一步发掘性质
\(dp\)的转移形式似乎暗示着可以使用网格建立模型，那么我们可以得到：
有一个网格\(A\)，\(A_{i,j} = [X_i < Y_j]\)，\(1\)表示能走，\(0\)表示不能走，能否从\((1,1)\)走到\((n,m)\)
那么以\(Y_{min} \leq X_{min}\)为例，反应到网格上就是\(\forall i \in [1,n],(i,pos[Y_{min}])\)都是堵死的，也就是走不到。另一个同理
把条件反一下呢？
如果\(Y_{min} > X_{min}\)，此时所有\(Y\)都比\(X_{min}\)大，即：\(\forall i \in [1,m],(pos[X_{min}],i)\)全是通路，另一个同理，\(\forall i \in [1,n],(i,pos[Y_{max}])\)全是通的，形如
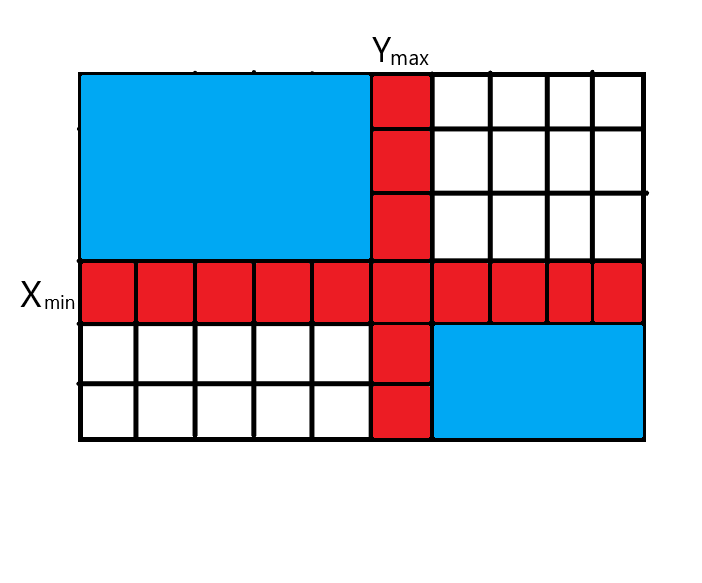
此时已经变成了左上和右下两个子问题（特殊性质只有左上），那么递归处理即可
这是左上的check，pre是前缀最值，右下check只需把pre改成suf并修改边界即可
bool chk1(int posx,int posy)
{
if(posx == 1 || posy == 1) return 1;
node X = prex[posx - 1],Y = prey[posy - 1];
if(x[X.mn] < y[Y.mn]) return chk1(X.mn,posy);
if(x[X.mx] < y[Y.mx]) return chk1(posx,Y.mx);
return 0;
}
丁香之路
个人认为不是很优美。。。
想到应该构造形如下图状物
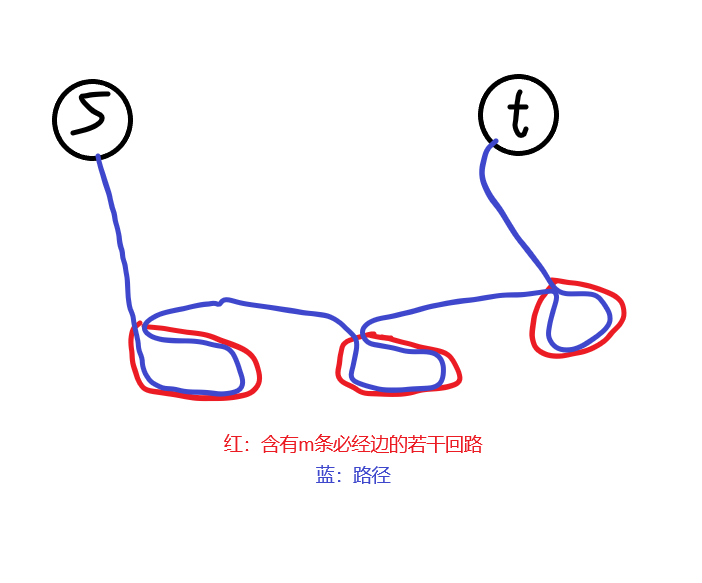
首先建出\(m\)条边，然后考虑怎么贪心
然后就有神秘小策略：如果当前点为奇点，就往下一个点（编号相邻）连边，如果下一个点变成奇点，则继续往后连，直到没奇点
就是先把所有点捏成若干个红圈圈。造完之后考虑连通性。可以使用最小生成树，但是要注意的是代价是树边和的两倍，因为此时的路径形如\(dfs\)，一条边走两次
最后起终点也要连边。。。
数学
Small Permutation Problem (Easy Version)
转化题
将排列转化为\((i,p_i)\)，那么就变成了\((i,i)\)与原点形成的矩形中有\(a_i\)个点，那么每次\(a_i\)变化就是在两个正方形形成的\(L\)形中加点（这也说明\(a_i\)单调不降）
考虑到排列形成的点横纵坐标各不相同，所以一个\(L\)里最多两个点，因此\(|\Delta a_i| \leq 2\)，可以判断有无解
然后如果差为\(1\)，那么只用在\(L\)的一支上加点，而上一个正方形占掉了\(a_{i-1}\)个横纵坐标，所以方案数为\(2(i - a_{i - 1}) - 1\)，减一是因为\((i,i)\)重复算了
类似的可得，差为\(2\)就是\((i - a_{i - 1} - 1)^2\)，因为\((i,i)\)一定不能填点
最后，判断无解还有首项不大于\(1\)和末项必须为\(n\)的要求
乘法原理统计即可
Multiple Lamps
人类智慧构造题。。。
很快就能想到一个灯最后能亮的条件是按下的按钮编号中有奇数个是其编号的因数
然后发动传统艺能人类智慧：将\(1\)到\(n\)全按一遍，最后亮的就是完全平方数
然后你就会发现在\(n \geq 20\)的时候就符合题目条件了。。。
so直接状压预处理剩下的\(n\)然后每次询问\(check\)预处理的合法状态即可
wtf
方案数
做了前置题后这道题就好做一些了 （别问前置题怎么找到的），设\(dp_i\)表示不经过其他障碍到达障碍\(i\)的方案数，原理和前置题相同
然后处理判定以及该题下的“距离”，那么就需要一个辅助数组\(g_{i,j,k}\)来表示当三个维度二进制下\(1\)的个数分别为\(i,j,k\)时的方案数，枚举每一位转移即可
如下，组合表示新加的$1$的分布情况
g[0][0][0] = 1;
for(int i = 0;i <= 60;i++)
{
for(int j = 0;j <= 60;j++)
{
for(int k = 0;k <= 60;k++)
{
if(i == 0 && j == 0 && k == 0) continue;
for(int x = 1;x <= i;x++)
g[i][j][k] = (g[i][j][k] + g[i - x][j][k] * C[i][x] % mod) % mod;
for(int x = 1;x <= j;x++)
g[i][j][k] = (g[i][j][k] + g[i][j - x][k] * C[j][x] % mod) % mod;
for(int x = 1;x <= k;x++)
g[i][j][k] = (g[i][j][k] + g[i][j][k - x] * C[k][x] % mod) % mod;
}
}
}
判定就按题意判定即可
Construct Matrix
很快发现要求每行\(1\)的个数奇偶性相同，列一样，那么奇数一定不行，然后\(k = n,k = n^2,k = 0\)较方便，不说，主要看偶数。偶数有两大类
- \(k = 4p\)
这个手摸\(n = 4,k = 8\)得到一个合法构造
当然还有别的，但这个规侓性很强，可以发现是由以下“基元矩阵”组成：
而且发现只要不重叠，随便怎么放都行，那就直接一个密铺过去
点击查看代码
int H = 1,W = 1;
while(k)
{
for(int i = H,oi = 1;oi <= 2;i++,oi++)
for(int j = W,oj = 1;oj <= 2;j++,oj++)
a[i][j] = 1;
W += 2;
if(W > n) H += 2,W = 1;
k -= 4;
}
print();
- \(k = 4p + 2\)
这个麻烦些，手摸\(n = 4,k = 10\)可得：
发现左上角那个\(3 \times 3\)可以把\(k\)的个数削成\(4p'\)，那么就可以继续沿用上面的基元矩阵密铺，不过\(3\)是个奇数，那就扩一圈\(0\)成为\(4 \times 4\)，然后去铺剩的。最后发现铺完后会剩\(4\)个或\(8\)个\(1\)，后者无解，前者扔进\(4 \times 4\)即可
I Wanna be the Team Leader
咕
字符串
字符串匹配
枚举循环节（\(AB\)）长度，算出能有多少节，然后暴力枚举节数和\(A\)长度，前者可以得到\(C\)，然后比对即可，有\(48\)分
枚举长度和节数是\(n\log n\)的，可以保留，考虑优化计算答案
发现每当长度加一，\(A\)的可能只增加一种，就是上一次的\(AB\)，然后可以预处理出前/后缀字符个数为奇数的字符数，每次得到\(C\)后开桶统计，枚举完当前长度后把当前长度扔进桶即可
复杂度\(O(26n\log n)\)，谷上过不去，要写树状数组？26和log26也妹啥区别吧
Short Code
建成trie树，然后把末尾标记点往空祖先跳，要求最小化标记点深度总和
就是把最深的往上提，注意不是直接让最深的跳到当前最浅（样例2过不去），而是从下往上一步一步跳，每次从儿子中选一个最深的跳
先搜在跳
void cal(int x,int d)
{
for(int i = 1;i <= 26;i++)
{
if(tr[x][i])
{
int k = tr[x][i];
cal(k,d + 1);
while(!q[k].empty()) q[x].push(q[k].top()),q[k].pop();
}
}
if(x != 1 && !cnt[x])
{
// cout << q[x].top() << endl;
ans -= q[x].top();
ans += d;
q[x].pop();
q[x].push(d);
}
}
串串题
很明显有两个性质：
-
\(B\)中出现的元素不能被删
-
\(B\)中没有且妨碍匹配（\(A\)中有）的要删掉
那么就可以把\([1,W]\)中所有\(B\)没有的算出来，记为\(All\)（这些都可以选），然后把\(A\)中在\(B\)出现的元素的下标提取出来，在扫这个下标序列的时候用双指针和桶维护要删掉的元素总数\(del\)（相当于一个长为\(m\)的滑动窗口），用\(KMP\)匹配，如果能配上，那么答案就是\(C_{All - del}^{d - del}\)，意即必选这\(del\)个数，然后再剩余中选够\(d\)个
Cezar
字典序 \(\to\) 拓扑，经典套路
就是按照\(a\)的限定，建\(S_{a_i} \to S_{a_j} (j > i)\)的边，具体的，找出\(S_{a_i},S_{a_j}\)第一个不同的位\(x\)，则有\(S_{a_i,x} \to S_{a_j,x}\)。如果没找见，而且\(S_{a_i}\)还比\(S_{a_j}\)长，则肯定无解。然后判环，跑拓扑即可
CSPS2023B消消乐
定义\(dp_{i}\)表示\([1,i]\)的子串的合法方案数，那么答案就是\(\sum\limits_{i = 1}^{n}dp_i\)
另定义\(pos_i\)表示使得\([pos_i,i]\)为合法串的位置，那么有\(dp_i = dp_{pos_i - 1} + 1\)。至于如何得到\(pos_i\)，可以类比\(next\)，初始化为\(i - 1\)，然后不断向前跳，即\(pos_i \to pos_{pos_i} - 1\)，直到\(s_{pos_i} = s_i\)
Keyboard Design
首先一个字符最多和两个字符相邻，扔到图上就是合法序列都是链，没有环。
所以可以先判环，扔掉不符合条件的单词，然后把剩下的串精简一下，因为我们只会关心相邻关系，像样例的\(abacaba\)就可以简化为\(bac\)，然后建\(AC\)自动机（多模式串匹配必备工具），注意相邻不分顺序，所以还要把串反过来再扔进去，然后经典小套路：\(W_{i} += W_{fail_i}\)以及经典小大炮：\(dp_{i,S}\)表示当前走到\(i\)节点，已经选择的字符集为\(S\)，式子很简单：
\(\large dp_{s | 2^j,tr_{i,j}} = \max(dp_{s,i} + W_{tr_{i,j}})\)
最后要输出方案，记录一下前驱状态以及前驱节点即可
Hossam and Range Minimum Query
奇偶性 \(\to\) 异或，还算经典
然后考虑到 \(3 \oplus 2 \oplus 1 = 0\)的坑，要赋随机权值来异或。然后区间内出现次数使用主席树来维护，询问的话在主席树上二分就行了
Comfortably Numb
考虑区间分治。设区间为\([l,r]\)，中点\(mid\)，假设最值在\([mid + 1,r]\)（在左边同理）
在\([mid + 1,r]\)内枚举右端点\(i\)，然后找到最靠左的左端点\(j\)使得区间最值\(mx\)不变（就是最值只能通过扩展\(i\)更新），设\(s_x\)表示前缀异或和，那么子区间最值就是在\(s_j,s_{j + 1},...s_{mid + 1}\)里选一个与\(s_i \oplus mx\)异或使得和最大，这个使用字典树维护
点击查看代码
void sol(int l,int r)
{
if(l == r) return;
int mid = l + r >> 1;
sol(l,mid),sol(mid + 1,r);
int mx = -1;
for(int i = 1;i <= tot;i++) tr[i][0] = tr[i][1] = 0; tot = 1;
rt = 1; sum[l - 1] = 0;
for(int i = l;i <= r;i++) sum[i] = sum[i - 1] ^ a[i];
for(int i = mid + 1,j = mid + 1;i <= r;i++)
{
mx = max(mx,a[i]);
while(j > l && a[j - 1] <= mx) j--,ins(sum[j - 1]);
int ret = sum[i] ^ mx;
ans = max(ans,ret ^ query(ret));
}
mx = 0;
for(int i = 1;i <= tot;i++) tr[i][0] = tr[i][1] = 0; tot = 1;
rt = 1; sum[r + 1] = 0;
for(int i = r;i >= l;i--) sum[i] = sum[i + 1] ^ a[i];
for(int i = mid,j = mid;i >= l;i--)
{
mx = max(mx,a[i]);
while(j < r && a[j + 1] < mx) j++,ins(sum[j + 1]);
int ret = sum[i] ^ mx;
ans = max(ans,ret ^ query(ret));
}
}
