模拟赛总结(二)

2024.8.1

T1 集合(mex.cpp)

枚举每个数，求他是\(mex\)的概率，就是取完比他小的，比他大的随便取的方案数比上总方案数

code

T2 取模(mod.cpp)

有点套路

定义：\(odd\)为奇数，\(even\)为偶数，\(num_{odd}\)或者\(t\)为奇数个数

那个下取整可以变为：

\[\begin{cases} & \text{ odd + even :} \frac{a_i+a_j-1}{2} \\ & \text{ otherwise :} \frac{a_i+a_j}{2} \end{cases}\]

那我们就分成两部分求：元素和和减了多少个\(1\)

在推正式的式子之前，先看一看对于固定的序列，有结论

\[\sum\sum \lfloor\frac {a_i+a_j}{2}\rfloor = (n-1) \sum a_i - num_{odd}(n - num_{odd}) \]

简单解释：考虑到是不重复的两两求和，那么每个元素都会和其他元素配对\(n-1\)次，然后结合一奇一偶配对会有一个\(-1\)，得到式子

接下来推正式的

• 元素和

考虑一个位置的贡献，当这个位置是\(val\)时，其他位随便取，\(m^{n-1}\)种序列，贡献就是一个\(val \times m^{n-1}\)，然后\(val \in [1,m]\)，共\(n\)位，所以

\[ans_1 = (n-1)\frac{m(m+1)}{2}m^{n-1}n \]

• 减一数量

假设当前有\(i\)个奇数，那首先分布有\(C_{n}^{i}\)种，设\([1,m]\)内有\(t\)个奇数，那么放奇数的位的情况有\(t^i\)种，相应的，偶数位有\((m-t)^{n-i}\)种，结合上面的结论可得贡献为\(i(n-i)\)，故

\[ans_2 = \sum_{i = 1}^{n-1}i(n-i)t^i(m-t)^{n-i}C_{n}^{i} \]

最后\(ans = ans1 - ans2\)

补上取余即可

code

T3 魔法(magic.cpp)

暴力给编号连边+\(bfs\)有\(60\)

正解：根据第二个传送法，我们可以把颜色相同的放到一起，如果两个编号间能传送，其实就是这两个编号代表的颜色联通了，可以使用类似并查集的方法合并，使用\(bitset\)实现状压，询问是\(O(1)\)的

小优化：假设当前颜色是\(i\)，那么合并到\(i-1\)就完了，因为更小的都已经并入\(i-1\)了

bitset: 一种容器 bitset<N> vis[N];。其中vis[i][j]表示第\(i\)个bitset的第\(j\)位

code

T4 排位(star.cpp)

贪心最多\(80\)

正解\(dp\)，戳它

code

2024.8.3

阿巴阿巴阿巴阿巴阿巴...

T1 怎么又是先增后减

对于最小的数字，它肯定去两边，那么交换次数就是左/右边比他大的数的个数，二者取\(\min\)，然后从小到大对每个点做一个这个即可

可以使用树状数组优化

code

T2 美食节

我们可以采取各种办法发现某些位置答案一样，而且构成连续区间

相关理解：

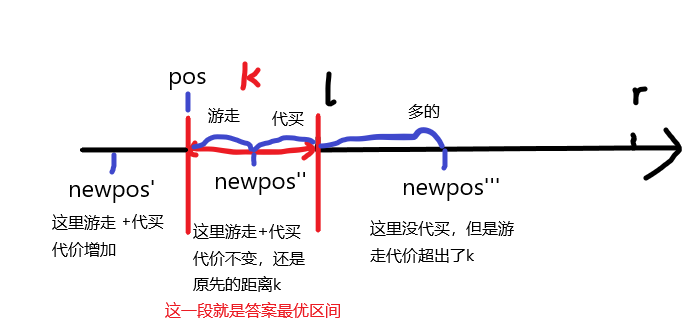
那么我们每次维护一个答案最优区间，每次和活动区间取交集，如果交集为空，就更新代价和区间

code

T3 环上合并

先说特殊性质

如果序列单增，则每个数都只需要一次操作，但是首尾不同，需要根据当前\(k\)的值讨论，具体情况手玩可得

竟然有60

然后我们就关注什么时候一个数需要一次操作，什么时候不止一次

为了方便讨论，我们新建一个数组\(b_i = sgn(a_i - k)\)

其中

\[sgn(x) = \begin{cases} 0 & x = 0\\1 & x > 0 \\ -1 & x < 0 \end{cases} \]

此时就要把数组全部染成\(0\)

那么讨论

• 形如\([0,1,1]\)或者\([0,-1,-1]\)，此时每个数只需一次操作

• 形如\([0,1,-1]\)或者\([0,-1,1]\)，此时必须额外花费一次

再将第二种情况扩展一下：\(-1,1\)交替出现时多消耗一次，所以找尽量长的交替段来计算额外答案

code

T4 送快递

大炮题

定义\(dp_{i,j}\)表示送完前\(i\)件后周欣，青蛙分别在\(a_i,a_j\)时的代价，那我们就根据上一件是谁送的来\(转移\)

以周欣为例

\[dp_{i,i-1} = \min_{j=0}^{i-1}(dp_{j,i-1} + |a_i - a_j|) \]

\[dp_{i,j} = \min_{j = 0}^{i-1}(dp_{i-1,j} + |a_i - a_{i-1}|) \]

又因为两人是等价的，所以把上面两维交换一下就是青蛙的式子

可得50

正解戳this

这里关于绝对值，由于只扫一遍，所以不知道内部大小关系，因此两种情况都要存，故需要两棵树，而且维护的时候要把整个含\(i\)的全扔进去

https://img2024.cnblogs.com/blog/1129554/202403/1129554-20240319111911135-280028134.png

2024.8.5

T1

最终态就是前面都为\(1\)，后面都为\(0\)，那么挪动总数就是所有\(1\)跑到后面的步数，又称逆序对数。\(10\)一次减少\(1\)，其余减少\(2\)。

假设值为\(l\)，如果\(l\)不是\(3\)的倍数，那么先手总能使得操作后\(l'\)为\(3\)的倍数，考虑到\(0\)也是三的倍数，所以先手胜（除非一开始就全是\(1\)）

同理，\(l\)是三的倍数时，后手胜

code

T2 珂学

每次选择的最大值肯定不挨着，那么操作总数就是被选择的数的总和

那么就有四种状态：左/右都/仅一个有（没有）被选择的数，代码中注释使用\(X\)表示

合并区间时，如果\(mid,mid +1\)都有被选择的数，就要分讨舍掉哪个数，被舍掉的数所在区间要用舍数后的状态更新

为了判断上面的情况，就要记录对应状态下左右端点的数是否被选择（没有就不管，也不更新）

code

T3 帝国飘摇

贪心，肯定越靠右越好，最劣情况就是第\(k\)大配第\(k\)小，倍增+归并维护每次扩张的区间，左端点更新为右端点\(+1\)

烦死了都在洛谷上过了怎么gxyz就是不让我过之前就有好几道题都是卡着最后一个点\(TLE\)还死活优化不过去把人气的又耗时间又耗心情真是的cnm老子的正解就TMD不是整洁了啊谁告诉你的我W#%@#

upd on 2024.8.8 : 开O2可过..........

T4 前往大都会

建最短路图搞大炮+鞋油

2024.8.6

T1 小学奥数题

膜拟了半天出不来，当场似了

\[ans = \max(\max\{a_i\},\lceil \frac{\sum a_i}{n} \rceil) \]

T2 BB

定义\(f(u,v)\)表示\(u\)是否支配\(v\)，即\(f(u,v) \in \{0,1\}\)

那么

\[\begin{align} ans &=\sum_{u\in A}\sum_{v \in B} f(u,v) - \sum_{u\in A}\sum_{v \in B} f(v,u) - \sum_{u \in A} w_u \\&= \sum_{u \in A}(\sum_{v \in B}f(u,v) + \sum_{v \in A}f(u,v)) - \sum_{u\in A}(\sum_{v \in B}f(v,u) + \sum_{v \in A}f(v,u)) - \sum _{u \in A}w_u \\&= \sum_{u \in A}(siz_u - dep_u - w_u) \end{align}\]

解释：赚的钱=从\(B\)那里收的保护费 - 给\(B\)的保护费 - 买点的花费

考虑到自己的点互相支配不影响赚的钱，所以用类似补\(0\)的操作修改前两项，然后发现前一项的\(f\)如果为\(1\)，\(v\)必然在\(u\)下面，所以\(v\)构成\(u\)的子树。类似的，第二项的\(v\)都是\(u\)的祖先，构成深度

算出来每个点的\(siz - dep - w\)后排序选择即可

code

T3 BC

理解大半，直接上马吧

高消版，也有纯大炮的

#include <bits/stdc++.h>
using namespace std; 
typedef long long ll; 
typedef unsigned long long ull; 
typedef double db; 
typedef pair <int,int> pii;
const int N = 1e3 + 5, M = 50 + 5, Mod = 998244353, inv = 205817851;
//first:概率 second:期望 
int n, m, W[M<<1]; pii F[N][M], G[N+M][M];
int Pow ( int x, int y ) { int res = 1; for( ; y; y >>= 1, x = 1LL * x * x % Mod ) if( y&1 ) res = 1LL * res * x % Mod; return res; }
int Inv ( int x ) { return Pow( x, Mod - 2 ); }
int Add ( int x, int y ) { return x + y >= Mod ? x + y - Mod : x + y; }
pii Add ( const pii& a, const pii& b ) {return make_pair( Add( a.first, b.first ), Add( a.second, b.second ) ); }
//加法取余，比较正常 
pii Mul ( const pii& a, const pii& b ) {return make_pair( 1LL * a.first * b.first % Mod, ( 1LL * a.first * b.second + 1LL * b.first * a.second ) % Mod ); }
//Mul：事件A,B期望的合并，E(A+B) = E(A)P(B) + E(B)P(A)
//这个和概率生成函数的导函数（某种情况下好像就是期望，E(x) = F'(1)）以及导数的运算法则有关
//实在不理解可以尝试使用集合描述法理解
//生成函数详情看看这个：https://www.cnblogs.com/gtm1514/p/16653405.html 
//F[i][j]：同题解含义 
//G[i][j]：最终值为(i,i+j)时的答案 
//+m是平移坐标
void Solve ()
{
	cin >> n >> m;
	for(int i = -m; i <= m; ++i ) cin >> W[i+m], W[i+m] = 1LL * W[i+m] * inv % Mod;
	//简化高消预处理F，O(nm^2)  
	//所谓的几何分布就是：该情况下期望是1/p或者(1-p)/p,p是概率（但是感觉在这里没什么用） 
	for(int i = 0; i < n; ++i)
	{
		pii T[M<<1];//高斯消元系数数组简化版，下标含义应当和F的第二维相等 
		for(int j = -m;j <= m; ++j) T[j + m] = make_pair(0, 0);
		for(int j = -m;j <= m; ++j) T[max(-i,j) + m] = Add(T[max(-i,j) + m], make_pair(W[j+m], W[j+m]));
		for(int j = -m;j < 0; ++j) 
			for(int k = 1; k <= m;++k) 
				T[j + k + m] = Add(T[j + k + m], Mul(T[j+m], F[i+j][k]));
		int tmp = Inv((1 - T[0 + m].first + Mod) % Mod);//这个手搓一下朴素高消版本就能知道是啥
		for(int j = 1;j <= m;++j)                                                                           //条件概率 
			F[i][j].first = 1LL * T[j + m].first * tmp % Mod, F[i][j].second = 1LL * ( T[j + m].second + 1LL * F[i][j].first * T[0 + m].second) % Mod * tmp % Mod;
	}
	//dp,将<i的答案向>=i转移 
	G[0][0 + m] = make_pair(1, 0);
	for( int i = 0;i < n; ++i)
		for(int j = max(-i,-m);j <= 0;++j)//起点 
			for(int k = 1;k <= m;++k)//向上“走”了多少步 
				if(k + j <= 0) G[i][k + j + m] = Add(G[i][k+j+m], Mul(G[i][j+m], F[i+j][k]));//此时用i+j的号打 
				else G[i+k+j][-(k + j) + m] = Add(G[i+k+j][-k-j+m], Mul(G[i][j+m], F[i+j][k]));//此时用i的号打 

	int res = 0;
	//答案的最终值范围是[n,n + m] 
	for( int i = n; i <= n + m; ++i ) for(int j = max(-i,-m); j <= 0; ++j) res = Add(res,G[i][j+m].second );
	cout << res << "\n";
}
int main ()
{
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0); Solve(); return 0;
}

T4 BD

直接戳吧，部分分，std都有

2024.8.7

困~~~~~

T2 排排

\(P_1 = 1\)启发我们可以从最值位置考虑，然后就很简单了，发现只有四种情况

• \(ans = 0\)：原本就单增，判一下即可

• \(ans = 1\)：比较复杂：根据第一个样例可知\(P_i = i\)的位置可以拿来操作，那么条件就是左边没有右边下标对应的数，可以用\(\max\)实现

• \(ans = 2\):\(1,n\)在中间，此时先操作一次可以把一个排到头头，然后变成\(ans = 1\)的情况

• \(ans = 3:\)：\(1,n\)在头头，但是反的，手算可知三次

code

T1 串串

对于一个点\(i\)，如果翻转后长度超过原串，判一下多出来的长度是否匹配即可

否则看一下新长度到达的点是否可行（倒着扫，因为\(len\)处肯定行），然后判一下多出长度是否匹配即可

code

T4 桥桥

思路很粗暴但不好想到

对操作分块，\(B\)次后处理，答案转化为并查集联通快\(size\)，暴力加边+撤回处理

细节见码子

T3 序序

戳

2024.8.8

T1 九次九日九重色

上古套路题

手摸样例配对的\({a,b}\)发现\(a\)按下标（不是值）排序时，\(b\)的下标单增

所以可以预处理所有可能的配对\((i,j)\)（都是下标），然后按\(i\)排序，对\(j\)做一个\(LIS\)

对于\(i\)相同的情况，按\(j\)逆序排序

预处理复杂度\(\sum_{i=1}^n\lfloor \frac{n}{i}\rfloor = n\log n\),\(LIS\)的二分\(DP\)也是这个复杂度

code

T2 天色天歌天籁音

想到莫队做法了，但是没想到好的求个数方法，套了个线段树\(O(n\sqrt n \log n)\)遗憾离场

然后发现想多了

题目要求区间众数的个数，并不关心是什么数，所以我们可以开一个数组\(num_i\)表示出现次数为\(i\)的有多少个

然后维护即可

code

T3 春色春恋春熙风

考虑回文成立当且仅当最多一个字母的个数是奇数，可以使用异或表示，每一位表示字母个数的奇偶性

那么\((u,v)\)点对合法就等价于

\[S_u \oplus S_v = 00..010...0或者0 \]

先说暴力：

对每个可能的状态(一共\(2^{22}\)种)开桶，从每个节点都搜一次，遍历时把符合该状态的点扔进去，并查找有无互补的点，有的话更新一下长度，平方级别有\(30\)

std:

考虑继承儿子的答案，那么为了省事，继承重儿子答案（因为子树最大，合并少），对于每个轻儿子暴力走一遍算出路径，其他信息都扔掉，数组留着维护重儿子信息

还有一个优化就是桶里直接装最深深度，直接算一下即可

当前树根\(x\)可能是\(lca\)，也可能不是（路径完全在子树内），所以要遍历儿子们更新路径

click here to see more details

T4 雪色雪花雪余痕

有两种方法：直接维护原序列或者维护差分数组

二者初始都是全为\(0\)

• 维护原序列

有两种加数方式：在后面一段区间加\(1,2,3..\)或者整体抬升

前者区间长是根号级别，然后可以使用类似背包的方式转移

注意有一种情况是前面一部分\(A_i\)递减，后面增加，这种情况可以从左向右移动最低点，然后左/右就会相应增加/减少相应的根号长区间，动态维护即可

• 维护差分数组

由于差分数组还原原序列做的是一个形如\(\sum i\times d_i\)的东西，所以\(dp\)方式有所不同

更多戳这里吧

2024.8.10

菜

T1 星际旅行

题意等价于：删掉两条走一遍的边后，剩下的是欧拉回路（这样才能都过第二次）

然后就有：两个自环，一个自环+一条边，两条有公共点的边三种，累计即可

注意要先判断图的联通，朴素并查集即可

code

T2 砍树

题目要求最大的\(d\)，使得

\[d \times\sum_{i=1}^{n}\lceil \frac{a_i}{d} \rceil \leqslant \sum a_i + k \]

然后发现二分死了

但是发现\(\lceil \frac{a_i}{d} \rceil\)的取值是根号级的，所以直接暴力枚举可能的除数并存储

注意，这里枚举的除数不一定是答案，而是当\(d\)大过一定值时，上取整的值不变，所以存的应是答案\(d\)的等价\(d'\)

然后反带回去验证即可

还有一个判断就是除出来的\(d\)要大于等于选的\(d'\)

code

T3 超级树

超级抽象

定义\(dp_{i,j}\)表示当前是\(i\)级超级树，内部同时含有\(j\)条无交点的边

很抽象，拿样例来说，\(j = 2\)时，类似\((1),(2-3)\)是符合定义的

然后考虑把两个\(i\)级超级树加一个根并成\(i+1\)级来转移

如果两棵树内部路径分别是\(l,r\)条，那么不考虑根节点时，就有\(num = dp_{i,l} \times dp_{i,r}\)个方案

然后要讨论根节点的去处

• 啥也不干，\(dp_{i + 1,l + r} += num\)

• 自己独立作为一个路径，\(dp_{i + 1,l + r + 1} += num\)

• 连到左/右子树内的一条路径上，共\(l + r\)种，又分方向，故有首位之分，\(dp_{i + 1,l + r} += num \times 2(l + r)\)

• 联通左右树的一条路，此时总数减一，然后乘法原理+方向可得\(dp_{i + 1,l + r - 1} = num \times l \times r \times 2\)

• 联通一个子树内的两条路，类似的可得\(dp_{i + 1,l + r - 1} = num \times (l(l - 1) + r(r - 1))\)

答案\(ans = dp_{k,1}\)

然后讨论循环上界，因为裸的上界是2的幂次

如果目标状态是\(dp_{m,q}\)，那么第二维\(\geqslant m + q + 1\)的状态肯定毫无意义，那么考虑到最终状态是\(dp_{k,1}\)，那么\(l + r\)肯定不超过\(k + 1\)，可以拿这点去卡，就能卡成\(k^3\)

code

T4 成绩单

啊，1.题读错了，暴力写炸了 2. n 最多50 四次方没想区间大炮

here here

code

2024.8.12

T1 序列

因为\(q \leqslant 1000\)，所以直接预处理\(q\)的整数次幂以协助找最小公比，然后暴力，前两项确定公比，然后加数就行了，注意\(q = 1\)的情况

code

T3 建造游乐园

以为是结论，但是是半结论

我们可以直接求欧拉图数量，然后删（加）一条边即为题目所求，共\(C_{n}^{2}\)种方法

考虑容斥

设\(g_i\)表示每个点的度数都是偶数，但图不一定联通的数量，\(f_i\)表示答案

对于\(g_i\)，构造方法是在\(i - 1\)个点中间任意连边，然后把度数为奇数的点都连向\(n\)，由于度数总和一定是偶数（每个边贡献\(2\)），所以这样是对的。每个边有连与不连两种情况，共\(C_{i - 1}^{2}\)条边，所以

\[g_i = 2^{C_{i - 1}^{2}} \]

然后要减去不联通的

不妨把图划分成两部分，第一部分一定联通，大小为\(j \in [1,i - 1]\)，第二部分不一定联通，大小为\(i - j\)，后一部分方案就是\(g_{i-j}\)，前一部分就是\(dp_j\)，考虑到前一部分联通大小至少为\(1\)，不妨固定一个点进去，剩下\(j - 1\)个点从\(i - 1\)个点中选，则

\[f_i= g_i - \sum_{j = 1}^{i - 1} dp_jg_{i - j} \]

\(ans = f_n\)

T2 熟练剖分(tree)

大炮，注释代码里有

code

T4 由乃的 OJ

病娇一般的题目and时空限制

\(30\)分就是贪心，从高到低，\(\&\)遇\(1\)取\(1\)，剩下两个都是遇\(0\)取\(1\)

std:

首先位运算不满足交换律，因此运算有顺序

然后\(2^{64}\)要开\(ull\)

大致思路就是拆成位，然后为了空间把64个位（64个线段树）压成一个\(ull\)拿线段树维护，初始每一位都是\(0/1\)，然后用一堆位运算搞

树剖的时候要两个方向

没过，看看

2024.8.13

T1 那一天我们许下约定

暴力\(30\)，然后大炮

设\(dp_{i,j}\)表示前\(i\)天给了\(j\)块饼干的方案，虽然\(D\)很大，但真给的天数不超过\(n\)，然后就变成\(O(nm)\)的了

答案就是\(dp_{i,n} \times C_{D}^{i}\)

后面那个递推可搞

code

T2 那一天她离我而去

拆掉\((1,i)\)，然后跑\(1 \to i\)的最短路再加上删掉边的边权就是小环，暴力枚举有\(40\)多

然后考虑不把边删掉而是连向虚拟点\(n + 1\)，具体的，将与\(1\)相连的边分为连到\(1\)或者连到\(n + 1\)，跑一次最短路就行

由于点编号不同，可用位运算分类

ps1:边的数量最多\(8e4\)，直接\(1e5\)得了

ps2:连向\(n + 1\)的边要在原图中删掉

code

T4 战争调度

暴力枚举叶子\(20\)

考虑枚举父亲状态然后到叶子时初始化，然后回溯时大炮

设\(dp_{i,j}\)表示以\(i\)为根的子树的叶子中有\(j\)个人打仗，那么就是\(dp_{i,k + l} = dp_{ls(i),k} + dp_{rs(i),l}\)

code

T3 哪一天她能重回我身边

考虑反面向正面连边，那么合法的情况就是每个点入度不超过\(1\),翻转就是改变边的方向，形成若干联通块

根据抽屉原理，边数 \(>\) 点数时一定有一个点入度为\(2\)，一定不合法，那么剩下的就是树或基环树，每个块内大炮求翻转次数最后汇总即可

click to get more details

2024.8.14

4道T4,吃满暴力就能上三位数

T1 2-Coloring

上来一道紫

暴力：\(30pts\)，状压枚举每一行的状态check即可

思路难泵，戳这里看第一篇，讲的清楚

code

T2 连通块

暴力:\(60pts\)，每次搜整个块即可

trick:删边改为加边，就是初始时把标记的未删的边合并，然后离线倒序跑询问，用并查集维护树的直径

答案就是查询点到块内直径其中一端的距离

code

T3 军队

暴力:\(20pts\)，模拟，上限在于数组大小和\(c\)的限制

重叠矩形使用扫描线，可以\(log\)处理出每行多少雌的，然后设\(x\)表示雌雄数量中较小者，然后它和\(\lfloor \frac{y}{2} \rfloor\)的大小关系不同时有不同的计算式子，可以使用前缀和优化成\(O(1)\)

code

T4 棋盘

暴力：\(0pts\)，宽搜爆完，但听说大炮有\(30\)

奇怪的维护，戳

2024.8.15

T1 Kanon

\(40pts\):开两个变量记录向左/右最远跑了多少，如果一个球当前位置超过原位置+最远距离就可能产生贡献，说可能是因为当前位置可能越过上一个球的历史位置，此时没贡献

考的时候想成一堆球打架就不会维护了qwq

code

\(100pts\)

每个雪球大小来源都是连续区间，没有交集那么答案就是区间长，有的话要判断交集属于哪个球，然后可以二分找到\(t\)，使得第\(t\)天无交集，第\(t + 1\)天有交集，则可得知交集是谁的

球之间的雪最需要判断主权，两端以外没必要（肯定是第一个和最后一个）

T2 Summer Pockets

讲解见the first one

code

T3 空之境界

裸区间大炮可以\(60pts\)

然后考虑转化：二分枚举答案，做\(01dp\)，表示区间内是否存在小于等于二分值的数，这样就能用bitset优化

然后将区间大炮的转移方式小改一下，就有两种情况：

• 更新\([i,j]\)，如果\([i + 1,j - 1]\)符合并且\(cost_{i,j}\)也符合条件，我们就能认定\([i,j]\)可行

• 用\([i,j]\)扩展，这一步有点像枚举断点更新，即如果\([i,j]\)符合条件，那么\([i,k]\)的状态（就是\([i,j]\)以后区间的状态）可以使用\([j + 1,k]\)更新

最后检查\([1,n]\)是否为\(1\)就行了

code

T4 穗/P4690 Ynoi2016

\(20\)的模拟 +\(20\)的普通莫队 + \(40\)的带修莫队

剩下\(20\)全踏马是珂技

2024.8.17

考场暴力刚好\(100\)

T1 Set

考场以为子集不连，直接乱搞起步睡到\(50\)

正解很简单：余数共\(n\)种，但前缀和\(s_0 \sim s_n\)一共\(n + 1\)个，所以找到相同的输出区间即可。。。

好短。。。

T2 Read

\(x\)本书可以“消”掉\(x + 1\)本书

那么如果有书的数量\(\geqslant \frac{n + 1}{2}\)，就说明有书会剩下，反之答案为\(0\)

考虑到\(a\)开不下，所以记一个\(val\)和一个\(sum\),\(sum\)为\(0\)时\(val = a_i\)，然后根据是否和\(val\)相同对\(sum\)加一减一，然后再生成一遍\(a\)记录\(val\)个数，如果满足有剩余的条件，答案就是\(x - (n - x + 1)\)

code

T3 题目交流通道

乱搞\(30\)

然后如果有\(d_{i,j} = d_{i,k} + d{k,j}\)，那么\(d_{i,j}\)的长度范围就是\([d_{i,j},k]\)共\(k - d_{i,j} + 1\)种，乘起来有\(60\)

考虑\(d_{i,j} = 0\)的情况，此时把\(0\)边连起来的点缩成一个（图论中曰为“团”），然后分团内和团外进行容斥，团内情况类似之前欧拉图构造的情况，式子也很像，然后团外（团与团之间，共\(siz_1 \times siz_2\)条边）的话还是找符合上面条件的\(d_{i,j}\)，如果有，那么之间的边随意，如果没有，那么至少一条长为\(d_{i,j}\)，也可容斥得出

code

T4 题目难度提升

构造

如果序列中间有数字出现两次以上，就一直让他作中位数，然后一小一大往里加即可

然后考虑一般情况

首先有结论：当前未填数的最小值必须大于等于当前中位数

那么就要看中位数情况，分加之前有奇数个/偶数个数字讨论

如果序列内没重复数字，那就走流程

如果有重复的，分析重复数字的位置，考虑在一定情况下让重复数字成为中位数

更多戳这里

code

附加：消除游戏

不会

2024.8.19

T1 电压

暴力拆边+check有\(25\)

然后要求删边后是二分图，那么删的边都在奇环上，考虑\(dfs\)生成树+返祖边check+差分搞

gxyz第一男神wmw题解

code

T3 奇迹树

一眼树的直径，想从某一端点出发搜完整棵树完成赋值

裸搜，假的，\(12pts\)

假了的原因在于不能保证其他点和作为终点的端点关系合法

处理很简单，先把不在直径上的点遍历完再给直径上的点赋值，很容易证明这样最优（考虑回溯，在直径上回溯然后跑到别的点肯定垃圾）

code

T2 农民

默认\(1\)为根全死了

修改后的暴力高达\(80\)

std:考虑维护每个点能吸收的肥料值的范围，一个节点会把\([l,r]\)分成\([l,w_u)\)和\((w_u,r]\)，然后一个点吸收范围就是祖先吸收范围的交集，使用线段树维护即可

code

T4 相逢是问候

click

2024.8.20

又双困了一上午╯﹏╰....

T1 博弈

先手必胜：至少一个数个数为奇数

奇偶性使用异或表示，但考虑到\(3 \oplus 2 \oplus 1 = 1\)，所以要先\(hash\)，然后考虑容斥，状态相等的点之间不合法，减去即可

code

T3 大陆

做过的原题，这里有

T2 跳跃

考虑到最优肯定是在某些区间里反复横跳，设\(l_i\)表示以\(i\)为右端点，和最大时的左端点

那么就是在\([l_{i_1},{i_1}],[l_{i_2},{i_2}]...\)的区间里跳

为了维护跨区间的跳跃，分别维护从\(1\)跳到\(i\)所需的最小步数和此时对应的分数，不足\(k\)的部分在\([l_i,i]\)内反复横跳，然后枚举上一个横跳区间，算出从那里跳过来时需要的步数以及对应分，考虑到方向问题，要奇偶判断一下，然后扫一遍就行

code

T4 排列

暴力\(40\)

剩下平衡树，不会

2024.8.21

Fate

看到教堂自动浮现名场面

暴力\(only\) \(19pts\)

大炮，设\(f_i,g_i\)表示从\(s\)到\(i\)的最短路径，最短+1路径的条数,\(dijkstra\)预处理dis

\[\begin{cases} f_u \to f_v & dis_v = dis_u + 1\\ g_u \to g_v & dis_v = dis_u + 1\\ f_u \to g_v & dis_u = dis_v \end{cases}\]

记搜转移即可

code

T2 EVA

睡了\(v\)相同的部分

考虑到以鱼的坐标为网的一端一定不劣，所以枚举鱼作为参考系，其他鱼根据相对运动可以算出进入网的时间范围，由于是\(double\)类型所以离散化一下，然后区间差分找使\(\sum w\)最大的时间点即可

code

T3 嘉然登场

状压\(40\) + \(K = 1\)的\(20\) \(= 60\);
考虑根据\(a_i\)的大小和与\(\frac{k}{2}\)的差的绝对值为排列依据降序排列，前面一部分抽象为\(1\)，后面抽象为\(0\)，和\(K = 1\)的情况类似，详细证明戳这里

code

T4 Clannad

爆了

题目要求包含区间内所有关键点的最小联通子树

有结论：

将关键点按\(dfn\)序排序后，边数 \(=\) \(\huge\frac{\sum\limits _{i = 1}^{k- 1}dis(a_i,a_{i+1}) + dis(a_k,a_1)}{2}\)，点数\(=\)边数\(+1\)

可结合\(dfs\)顺序理解

依此暴力\(40\)

然后可以使用回滚莫队(只删不加) + 链表（删除\(O(1)\)）维护，检查祖先的\(log\)使用\(dfn\)序\(——ST\)表优化成\(O(1)\),\(O(n\sqrt n)\)然后再小卡一下(__lg和交换\(ST\)两维)

code

2024.8.22

今天题难，才爆出来\(60\)多

对应的讲解戳题可得

或者这个

T1Skip

暴力：\(30pts\)

这个代码用魔法常数可得\(60\)

T2String

code

T3Permutation

暴力大炮：

code

std:

code

T4小P的生成树

参考这个严谨一点

code

2024.9.8

大数学时代

T1 喜剧的迷人之处在于

首先找出使\(ax\)为平方数的最小\(x\)，分解质因数即可实现，然后二分找一个平方数\(pf\)使得\(x \times pf\)在范围内即可

后面三道就乱杀人了

戳戳

T2 镜中的野兽

本质是容斥，但是朴素版本会算死人的，所以开科技（莫反）

code

T3 我愿相信由你所描述的童话

正反两遍平方级大炮跑最长子序列类似的板子然后没去重死了

重复原因就是统计答案时在枚举坡度转折点\(t\)，如果中间是平的就\(gg\)了

T4 Baby Doll

一眼顶针鉴定为神秘外星禁忌知识根本不可做

2024.9.15

我是盲人

T1 出了个大阴间题（repair

瞎 * 1，看成自由合并，然后被求\(b\)难倒，事后才发现每次的\(b\)都是\(2^{k - 1} - 1\)...

部分分（80pts）:

定义\(dp_{i,S}\)表示当前最大值为\(i\)，合并状态为\(S\)的代价和，\(i\)的范围最大到\(\max(a_i) + n \leqslant 2n\)，然后模拟就行

考虑到题目说的是排列，而状态只能表示选没选，所以还得另开一个存方案数

std:

可以预处理每个状态下的最大\(a\)，然后实际合并到此状态的\(a'\)无非就是相等或差\(1\)，所以上面\(dp\)的的第一位直接改成\(2\)表示对应情况，其他没什么改变

code

T3 是我的你不要抢（string）

瞎 * 2，看成\(S\)尾部的倒序了...

想到自动机的fail可以搞，但是好像要撤销，不会了

后边发现hash+记录答案可过...

至于原理，考虑最多只有\(n^2\)种不同询问，\(n^2 > Q\)的话就是\(Q\)，复杂度\(O(\frac{Q\sum len}{n})\)，反之复杂度就是\(O(Q\sum len)\)，两种都是\(O(\sum len \sqrt{Q})\)级别的，可过

然后\(map\)会被卡\(T\)，纯\(ull\)会卡\(WA\)，对应用\(un-map\)和取余再哈希解决即可

code

T2最简单辣快来做（satellite

瞎 * 3，没看到\(ans\)没清空暴力似了

绝对值拆成四个方向的矩形维护

对于每个卫星相对查询点所在的四个矩形哪一个的序列，只有\(O(n^2)\)种可能 的情况。 也就是对于卫星\((x_i,y_i)\)用直线\(x = x_i\)和\(y = y_i\)将平面分割成\(O(n^2)\)个格子。 如果查询点落在直线上，根据绝对值性质直接选择任意一个相邻的矩形。 如果落在格子里，就直接选择对应的矩形。 类似之前的二维前缀和，在直线的每一个交点处求出四个方向矩形的和。 在查询的时候，通过先前的离散化找到对应的格子，然后利用O(log v) 快速幂（实测88pts），或者是分块预处理的O(1)光速幂，计算出查询点到格子四个角的额外贡献

code

T4 显然也是我整的

好像是每次找到一些单独成块的点（这里的点可能是单点，也可能是缩完的点）计入答案，然后构造 + 递归搞

具体还是不太清楚