AC Automaton
0.什么是自动机
1.实现原理
\(TRIE + KMP\),详细戳这里
本质:字符串图论
这里重点看代码实现
#include<bits/stdc++.h>
#define N 1000005
using namespace std;
int T,n;
char s[N],t[N];//模式串、文本串
namespace AC
{
int tot;
int tr[N][27];//字典树(图) ,u ->i-> tr[u][i] i是字母的编号
int rev[N];//对应的编号,主要是应对重复串:把重复了的第j个串对应的编号赋成前面出现过的第i个串
int fail[N], idx[N], in[N], vis[N], ans[N];
//点u的 fail指针、是第几个串的结尾、(fail指针的)入度 答案数组 插入时被字符串"经过"的次数
void init()
{
memset(tr,0,sizeof(tr));
memset(fail,0,sizeof(fail));
memset(idx,0,sizeof(idx));
memset(in,0,sizeof(in));
memset(vis,0,sizeof(vis));
memset(ans,0,sizeof(ans));
memset(rev,0,sizeof(rev));//初始化(可能会T(doge))
tot = 1;//根节点编号为1,后续节点编号从2开始
}
void insert(char x[],int id)//建字典树
{
int u = 1;
int l = strlen(x + 1);
for(int i = 1;i <= l;i++)
{
if(!tr[u][x[i] - 'a']) tr[u][x[i] - 'a'] = ++tot;
u = tr[u][x[i] - 'a'];
}
if(!idx[u]) idx[u] = id;//记录首次以u结尾的串的编号
rev[id] = idx[u];//处理重复串,当前第id个串重了的话对应的就是第idx[u]个串
return;
}
queue<int> q;
void build()//拓扑排序优化用fail指针建字典图
{
for(int i = 0;i < 26;i++) tr[0][i] = 1;
q.push(1);
fail[1] = 0;//从根开始
while(!q.empty())
{
int u = q.front();
q.pop();
for(int i = 0;i < 26;i++)
{
int v = tr[u][i];
if(!v)
{
tr[u][i] = tr[fail[u]][i];//后面没了直接拿fail当新边
continue;
}
fail[v] = tr[fail[u]][i];//KMP思想,把v的指针指入tr[fail[u]][i]
in[tr[fail[u]][i]]++;//对应上一行,tr[fail[u]][i]的指针入度增加了一个fail[v]
//cout << in[tr[fail[u]][i]] << endl;
q.push(v);
}
}
}
void topo()//拓扑搞答案
{
for(int i = 1;i <= tot;i++)
if(!in[i]) q.push(i);//拓扑套路
while(!q.empty())
{
int u = q.front();
q.pop();
vis[idx[u]] = ans[u];
int v = fail[u];
ans[v] += ans[u];//合并点的答案
in[v]--;
if(!in[v]) q.push(v);
}
}
void query(char x[])
{
int u = 1,len = strlen(x + 1);
for(int i = 1;i <= len;i++) u = tr[u][x[i] - 'a'],ans[u]++;//更新ans数组
}
void getans()
{
int sum = 0;
for(int i = 1;i <= n;i++) printf("%d\n",vis[rev[i]]);
}
}
int main()
{
scanf("%d",&n);
AC::init();
for(int i = 1;i <= n;i++) scanf("%s",s + 1),AC::insert(s,i);
AC::build();
scanf("%s",t + 1);
AC::query(t);
AC::topo();
AC::getans();
return 0;
}
对应的是板子题
2,应用
纯自动机
P3966 [TJOI2013] 单词
开始没看懂题
结合英文写作常识才知道文章是(样例为例)
有空格隔开的不能算做一个单词
那是不是就这样每输入一个单词就加个空格来生成文本串最后再统一与模式串(单词)匹配即可?
按理来说是这样的,得到了\(90pts\)(模拟空格的是"{",即ASCII表中z的后一个字符)
后来才发现这样做文本串会膨胀到\(10^6 + 200\),还得多开个\(200\)多的空间
#define N 1005005//内存开大
...
void init(char x[])
{
int l = strlen(x + 1);
for(int i = 1;i <= l;i++) t[++cnt] = x[i];
t[++cnt] = '{';
}
...
//剩下的都是上道题的板子
P5231 [JSOI2012] 玄武密码
这里要求的是最长前缀,本来想着只靠\(TRIE\)也行,后来发现缺的要素太多,比如当前匹配不上要记录长度时该把答案归到哪个模式串头上,同时沿着树向下进行类\(dfs\)操作时不把答案记乱的一些细节等等
那我们不妨利用下\(AC\)自动机里的成分
这里,\(fail\)指针成为一个利器,因为结合含义,他可以用来记录哪些前缀(不一定最长)出现在了文本串中(\(fail\)可能跨串,如下图,也可能像\(KMP\)一样在同串之间跳)
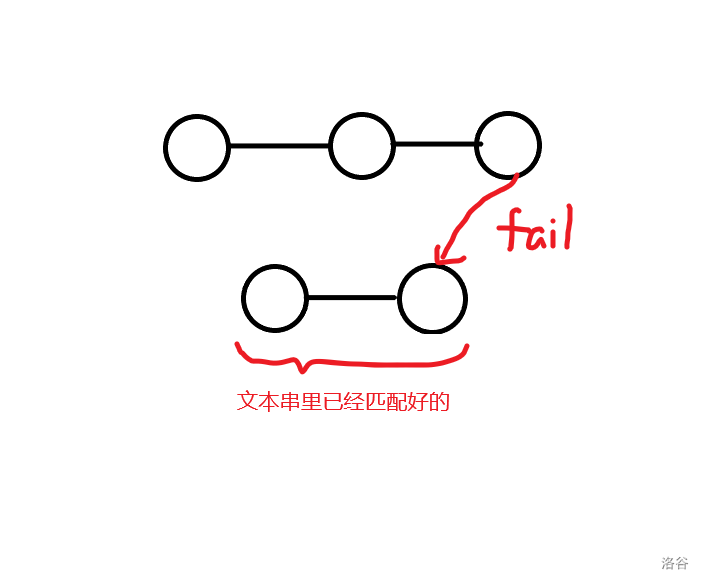
那么用\(fail\)打完标记后,对于每个模式串,就可以通过在\(TRIE\)上找标记点来得到最长的前缀了
void build()
{
for(int i = 1;i <= 4;i++) tr[0][i] = 1;
q.push(1);
fail[1] = 0;
while(!q.empty())
{
int u = q.front();
q.pop();
for(int i = 1;i <= 4;i++)
{
int v = tr[u][i];
if(!v)
{
tr[u][i] = tr[fail[u]][i];
continue;
}
fail[v] = tr[fail[u]][i];
q.push(v);
}
}//板子
int p = 1;
for(int i = 1;i <= lent;i++)
{
p = tr[p][getid(t[i])];
for(int k = p;k && !vis[k];k = fail[k]) vis[k] = 1;
}//用文本串跑trie,通过fail标记出现了的前缀
}
void getans()
{
for(int i = 1;i <= m;i++)
{
//每个文本串跑一边trie找最远的标记点
int res = 0;
int l = strlen(s[i] + 1);
int p = 1;
for(int j = 1;j <= l;j++)
{
p = tr[p][getid(s[i][j])];
if(vis[p]) res = j;//j单增,就这样写
}
printf("%d\n",res);
}
}
P2444 [POI2000] 病毒
输出TAK白拿60
有点莫名其妙
画了个大图才明白
一个病毒出现的充要条件就是当前点\(p\)跳到了某个串的尾巴上,那么如果不想让病毒出现,就需要找到一条长度无限的路径,该路径不经过所有病毒串的尾巴节点
长度无限,就是在环里兜圈子
所以就是看字典图上是否存在一个环,该环不经过所有病毒串的尾巴节点
以题干中的一组病毒为例
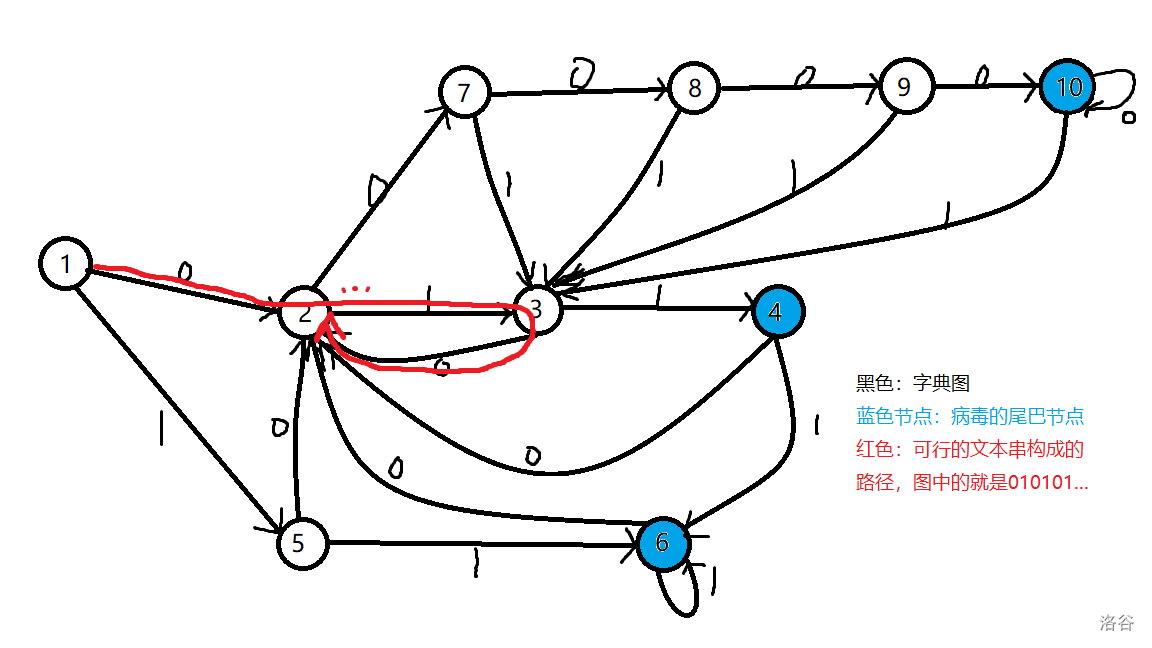
那么用搜索找符合条件的环即可
//超原始代码
//tr已经经过AC::build()了
void dfs(int x)
{
if(vis[x] == 1)
{
ans++;
return;
}
vis[x] = 1;
for(int i = 0;i <= 1;i++)
{
int u = tr[x][i];
if(vis[u] == 2) continue;
dfs(u);
vis[u] = 0;
}
}
//44pts
优化:另开一个数组记录当前点是否在搜索路径上,在搜索完毕时进行重置
void dfs(int x)
{
ifvis[x] = 1;//将当前点记为在路径上
for(int i = 0;i <= 1;i++)
{
int u = tr[x][i];
if(ifvis[u])//下一步就在该路径上
{
ans++;//有合法环
return;
}
if(!wei[u] && !vis[u])//
{
vis[u] = 1;
dfs(u);//继续沿该路径找
}
}
//此时出了循环,说明上一条路径搜完了,重置标记
ifvis[x] = 0;
}
怎么才\(76pts\)
这和上面的一张图有关

如果下面一行的后一个节点是尾巴节点呢?
说明上面一行的最后一个即使不是尾巴节点也不能走
所以要根据\(fail\)多打标记
if(!v)
{
tr[u][i] = tr[fail[u]][i];
if(vis[fail[u]] == 2) vis[u] = 2;//根据fail打标记
continue;
}
fail[v] = tr[fail[u]][i];
if(vis[fail[u]] == 2) vis[v] = 2;//根据fail打标记
q.push(v);
以此可见\(fail\)指针的一个重要含义:指向的是当前已匹配的最长后缀
奇美拉
\(dp\)常用定义:\(dp_{i,j}\)表示当前文本串长度为\(i\),走到了自动机上标号为\(j\)的点
可附加其他状态
P2322 [HNOI2006] 最短母串问题
\(dp\)+状压+字符串匹配
状压有点像Bill的挑战
现在就是要把这东西放到自动机上
众所周知匹配上一个串就是经过他的尾巴点,那么我们就在跳到尾巴时把对应编号位搞成\(1\)
S[u] = 1 << (id - 1);
这里再结合\(fail\)的含义,还要把\(fail\)两端节点的状态合并一下(不写\(80pts\))
S[u] |= S[fail[u]];
然后\(bfs\),每走到一个点就继承(按位或)一下他的状态,直到继承完所有模式串结束的状态
然后就得到超暴力\(50\)分代码
很显然,存储方式太\(low\)了
事实上,一般的\(dp\)问的是最小长度,那很明显,这题还要用记录路径的方法来搞答案
原先的代码就像\(dfs\)一样把信息都扔进了队列,浪费空间,所以采用新的方法
不妨记录每次的跳动是在第几次的跳动上进行的,所以设\(fa_i\)表示第\(i\)次跳动是在第\(fa_i\)次跳动进行的
分散的跳动都聚在循环内部,所以出了循环才相当于进行了一次大的跳动(换了一个分散点)
最后再根据路径还原串,然后倒序输出即可
这里还用到了\(bfs\)的优势:考虑到每一次循环都是按字典序来的,所以一旦找到了第一个答案,毫无疑问一定是最短且字典序最小,此时输出完后直接退出即可
void solve()
{
vis[1][0] = 1;//vis[u][s]表示节点u的状态为s的情况是否已经遍历
node tmp;
tmp.idx = 1,tmp.nowS = 0;
q1.push(tmp);
p = 0;//记录大的跳跃
while(!q1.empty())
{
node u = q1.front();
q1.pop();
if(u.nowS == ((1 << n) - 1))
{
while(p)
{
//printf("p:%d\n",p);
ans[++sum] = path[p];
p = fa[p];
}//回溯路径
for(int i = sum;i >= 1;i--) printf("%c",ans[i] + 'A');
return;//直接退出
}
for(int i = 0;i < 26;i++)//这里面所有的跳跃(push了的)都是在第p次跳跃的基础上进行的
{
int v = tr[u.idx][i];
if(!vis[v][u.nowS | S[v]])
{
vis[v][u.nowS | S[v]] = 1;//打标记
fa[++cnt] = p;//意义如上
path[cnt] = i;//记录该次跳跃对应的字符
node x;
x.idx = v,x.nowS = u.nowS | S[v];
q1.push(x);//push新节点
}
}
p++;//小跳完了是大跳
}
}
坑点:重复串(不写\(90pts\))
S[u] |= 1 << (id - 1);
P4052 [JSOI2007] 文本生成器
这题写bfs10分
设\(dp_{i,j}\)表示当前串长为\(i\),在自动机上走到点\(j\)时的方案数
转移:\(dp_{i,j} \to dp_{i + 1,tr_{j,s}}\)
这样想了好久,后来发现无论如何都带有严重的后效性(因为不管能配上多少个,贡献只有一),所以要换个思路
显然总方案数就是\(26^m\),那么可以尝试求出不包含可读词的串数
那就可以参照上面病毒的解法,把能配上的点打上标记,\(dp\)时直接绕过这些点就行了
式子:\(dp_{i + 1,tr_{j,s}} += dp_{i,j}\)
初始化:\(dp_{0,1} = 1\),即在起点处,方案有一个(空串)
答案:\(26^m - \sum dp_{m,i}\)
坑点:写在新\(namespace\)里的变量不会像全局变量一样自动重置,得手动memset
void solve()
{
int ans1 = 1;
for(int i = 1;i <= m;i++) ans1 = (ans1 * 26) % mod;//总数
memset(dp,0,sizeof(dp));//手动清零
dp[0][1] = 1;
for(int i = 0;i < m;i++)
{
for(int j = 1;j <= tot;j++)
{
for(int s = 0;s < 26;s++)
{
int k = tr[j][s];
if(vis[k]) continue;//能匹配上就跳过
dp[i + 1][k] = (dp[i + 1][k] + dp[i][j]) % mod;//dp
}
}
}
int ans = 0;
for(int i = 1;i <= tot;i++) ans = (ans + dp[m][i]) % mod;//求和
int y = (ans1 - ans) % mod;
printf("%d",(y % mod + mod) % mod);
}
P4045 [JSOI2009] 密码
数量+方案,鉴定为最短母串大爸
不同的是,这道题加了母串长度的限制,所以可能一些重叠部分要展开,比如母串长为\(7\)时就要是\(goodday\)
所以需要大力\(dp\)
仿照上题,定义\(dp_{i,j,S}\)表示当前串长度为\(i\),走到了自动机上\(j\)号点,匹配上的串集合为\(S\)
式子和上题也极为相似
\(dp_{i+1,k,S | s_k} += dp_{i,j,S}\)
如果不考虑方案可以得到\(50pts\),且根据\(WA\)的地方都是\(line\) \(2\)可得第一行的总数都是对的
接下来考虑求得具体的串
题目说了,只在\(ans \leqslant 42\)时输出串,而数量是\(LL\)级别的,所以不能在\(dp\)的同时记录路径,考虑直接搜索出串
首先,模拟\(dp\),标记出可行的\(dp\)路径,然后再沿着标记走得到答案
bool dfs(int len,int idx,int nows)//找到路径
{
//vis:是否访问过(简直)
//can:是否在可行的路径上
if(len == L)
{
vis[len][idx][nows] = 1;
can[len][idx][nows] = (bool)(nows == (1 << n) - 1);//到了路径终点,看看是不是答案路径
return can[len][idx][nows];
}
bool u = 0;//记录从该点出发有没有在路径上的点
if(vis[len][idx][nows]) return can[len][idx][nows];//剪枝
else vis[len][idx][nows] = 1;
for(int i = 0;i < 26;i++)
u |= dfs(len + 1,tr[idx][i],nows | S[tr[idx][i]]);//找延伸出去的点中有没有路径点,找到至少一个u就是1,所以用|
can[len][idx][nows] = u;//记录是否找到
return u;
}
void getans(int l,int idx,int nows)//搞答案
{
if(!can[l][idx][nows]) return;//该点不在路径上的话直接叫停
if(l == L)
{
for(int i = 1;i <= L;i++) printf("%c",anss[i] + 'a');
printf("\n");//由于是顺序搜索,所以正序输出
}
for(int i = 0;i < 26;i++)
{
anss[l + 1] = i;//记录可能路径上的字母
getans(l + 1,tr[idx][i],nows | S[tr[idx][i]]);//按延伸点搜索
}
}
void solve()
{
memset(dp,0,sizeof(dp));
dp[0][1][0] = 1;//初始化,和上题一致
for(int i = 0;i < L;i++)
{
for(int j = 1;j <= tot;j++)
{
for(int s = 0;s <= (1 << n) - 1;s++)
{
for(int t = 0;t < 26;t++)
{
int k = tr[j][t];
dp[i + 1][k][s | S[k]] += dp[i][j][s];//也和上一道题一致
}
}
}
}
for(int i = 1;i <= tot;i++) ans += dp[L][i][(1 << n) - 1];//同理
printf("%lld\n",ans);
if(ans > 42) return;//ans大时不必搞串
memset(anss,0,sizeof(anss));
memset(vis,0,sizeof(vis));
memset(can,0,sizeof(can));
dfs(0,1,0);//先找路径
getans(0,1,0);//再找答案
}
P4569 [BJWC2011] 禁忌
标签最难蚌的一集
翻译:用前\(alpha\)个小写字母等概率生成一个长为\(len\)的串\(T\),定义贡献\(w(T) = x\)为将其分成(没有重叠) 若干部分,最多含有\(x\)个模式串,求\(E(T)\)
结合自动机是图论的暴论思想,这就是一个图上概率\(dp\),每个点的度都是\(alpha\)
老定义:设\(dp_{i,j}\)表示文本串长度为\(i\),走到了\(j\)点时的期望值
结合没有重复的限制,我们可以贪心的想到:如果要最大化\(w(T)\),肯定是配上一个后直接在后面拼一个尽量短的模式串
放在自动机上,就是直接返回根开启新一轮的配
我们可以根据这一点写出图上的期望\(dp\)
设\(tr_{j,s} = k\)
如果\(k\)是一个尾巴节点,则配完后回到根加新的
否则
但是\(len \leqslant 10^9\),肯定开不出来
我们不妨找到一个最小单元,再用这个单元还原出整个串
这个套路在矩阵乘法中十分常用
上面的\(dp\)就是从\(j\)走到\(k\)或者回到\(1\)
因此可以结合图论在矩阵上的体现形式来构造矩阵
首先搞一个\(tot \times tot\)的矩阵,一般情况下\(j,k\)之间有边要走,就把对应的值赋成边权,也就是\(\frac{1}{alpha}\)
接下来要考虑如何转化这个东西:
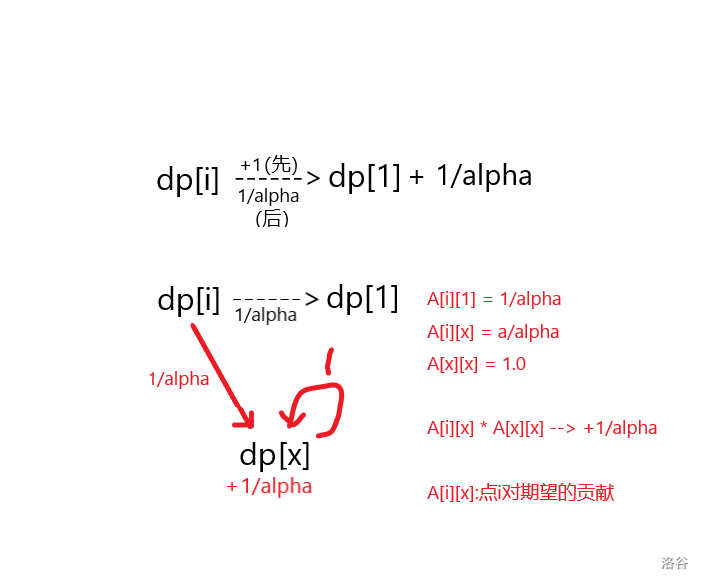
重点是分子多加了个\(1\),不是纯乘积,要想办法处理
先分割一下
前半部分就是老办法,把\(j \to 1\)对应部分加一个\(\frac{1}{alpha}\),
对于后半部分,考虑使用图论表示法
众所周知\(A_{i,k} \times A_{k,j}\)表示\(i \to j \to k\),那么对于\(+ \frac{1}{alpha}\),可以拆成\(\frac{1}{alpha} \times 1\),也就是要走过权值为\(\frac{1}{alpha}\)和\(1\)的边,那么中间点选什么呢?
首先\(1 \sim tot\)是不能用的,那些用来转移\(dp\)数组,使用其中的点会将两个和项混为一谈,那么不妨引入一个新点\(x\)来专门存储和项,那么走向就是\(i \to x \to x\),边权分别为\(\frac{1}{alpha}\)和\(1\)
- 为什么不是\(i \to i \to x?\)
因为\(i \to i\)会影响\(dp\)的转移
- 为什么边权不是\(1\)和\(\frac{1}{alpha}?\)
首先经过尝试这样是不行的,那么具体原因要结合因果关系:\(i \to x\)才是\(dp\)下的概率事件,\(x \to x\)是必然的,因为\(x\)就这一条出边
还有一种方式理解就是这里的\(x\)代替的就是\(tr_{i,s}\),是属于\(dp\)系统里面的东西,所以要把边权赋成概率
- 答案?
由于是以走完一遍图为最小单元来做矩阵乘法,所以答案就是\(A^{len}\)之后根节点的答案
到这里,其实矩阵大部分的思想都和GT考试如出一辙,所以在答案方面也会想着类比
原先的答案是\(\sum_{1}^{tot}dp_{len,i}\),换成矩阵就是\(\sum_1^{tot}A_{1,i}\) ?
不是的
我们再次想一想先前提到的一个重要东西——额外点\(x\)
结合\(dp\),可以发现所有的和项都存入了\(x\),由此可推测\(x\)应当与答案有关
事实上,做矩阵乘法时,会有\(\sum A_{i,x}\times A_{x,x},i \in [1,tot]\),这里相当于所有点都向\(x\)走了一遭,所以\(x\)更大的功能就是一个虚拟汇点
或者说,答案是在走的时候顺带着的,走到哪里,哪里就是答案聚集处,所以总路径就是\(根 \to 其他 \to 尾巴 \to 根/汇点\),所以答案在根和\(x\)处,那么需要在这两点之间再走一步来汇总,就能得到答案
所以
附:这里的\(x\)是大于\(tot\)的任意值
//x = tot + 2
matrix init()
{
matrix A;
for(int i = 1;i <= tot;i++)
{
for(int s = 0;s < alpha;s++)
{
int k = tr[i][s];
if(!vis[k]) A.m[i][k] += 1.0 / alpha;//非尾巴点在(i,k)间赋边权
else A.m[i][tot + 2] += 1.0 / alpha,A.m[i][1] += 1.0 / alpha;//要给(i,x),(i,1)赋边权
}
}
A.m[tot + 2][tot + 2] = 1.0;//那个小自环
return A;
}
int main()
{
scanf("%d%d%d",&n,&len,&alpha);
for(int i = 1;i <= n;i++)
{
scanf("%s",s + 1);
AC::insert(s,i);
}
AC::build();
matrix A = init();
matrix sum = qpow(A,len - 1);//快速幂
printf("%lf",sum.m[1][tot + 2]);//答案
return 0;
}
啸细节:自动机\(buff\)
vis[u] |= vis[fail[u]];
[BZOJ 2905]背单词
这题自动机优势明显

也就是说,若\(T\)是\(S\)的子串,那么总能通过跳\(fail\)调到\(T\)的尾巴节点
但是出现了一个小问题:序列是从短到长,而\(fail\)很明显方向反了
那就不妨把\(fail\)反着建一遍就行了,方便并答案
那么此时起点反而是子串\(S\)的尾巴点,终点是以\(S\)为子串的\(T\)中的某个节点- ---- ①
接下来我们考虑怎么转移答案
首先,反建\(fail\)后,一根串\(s\)会有一大堆\(fail\)指入该串字符对应的结点\(s_i\),结合①,可得选了\(s\),转移范围就是所有\(s_i\)的父亲(还有祖先),区间查询最大值后再决定加不加\(val_s\),得到\(ans_s\)
那么得到了\(ans_s\),所有以\(s\)为子串的串\(T\)自然也能得到这个答案,再结合①,可知还要对\(s\)的儿子,而且是由尾巴点的\(fail\)指向的儿子 进行修改,区间修改
这些操作可以用\(dfs\)序+线段树维护
while(T--)
{
init();//清空
scanf("%d",&n);
for(int i = 1;i <= n;i++)
{
int v;
scanf("%s",s + 1);
scanf("%d",&v);
insert(s,i);//插入
val[i] = v;
}
build();//建fail
for(int i = 1;i <= tot;i++) add(fail[i],i);//反建fail
ST.build(1,tot,1);
dfs(1);//获取dfs序
int ans = 0;//答案
int sum = 0;//一条串的答案
for(int i = 1;i <= n;i++)
{
sum = 0;
int u = vis[i];//从尾巴点开始遍历整个串
while(u)
{
sum = max(sum,ST.query(1,dfn[u],1,tot,1));//更新max
u = fa[u];//这里的fa是在insert()中更新的,就是一条串内一个字符结点的上级节点
}
u = vis[i];//只有尾巴点的子节点才能修改
sum = max(sum,sum + val[i]);
ans = max(ans,sum);
ST.add(dfn[u],out[u],1,tot,1,sum);//修改
}
printf("%d\n",ans);
}
然后喜提\(24pts\)
才没有什么query没return,add的比大小打成赋值,多测少清几个这种东西
仔细想想可以发现上面两个操作似乎有重叠的地方:修改操作就已经把\(T\)中节点的\(max\)修好了,那么查询的时候不必再找这些点的父亲,直接在节点中找\(max\)就行了
sum = max(sum,ST.query(dfn[u],dfn[u],1,tot,1));
喜提\(64pts\)
CaO
发现输出的答案都比std大,肯定还有重叠操作
后来发现真是重叠了——
TMD某个傻逼竟然用build()函数清空线段树,很明显由于每次tot不一样所以线段树大小不同,那肯定清不干净
6
void cle(){memset(t,0,sizeof(t));}
[ABC305G] Banned Substrings
病毒+禁忌,边权改为\(1\),不走尾巴点即可
不同的是,最终答案可以表示为\(1 \to id\),但这一步只有一次,不像禁忌的虚拟汇点,所以不能加入\(A\),必须另外乘一次汇总一次答案
matrix sum;
sum.m[1][1] = 1;
sum = cal(sum,qpow(A,n - 1));


 浙公网安备 33010602011771号
浙公网安备 33010602011771号