状压dp
0.位运算
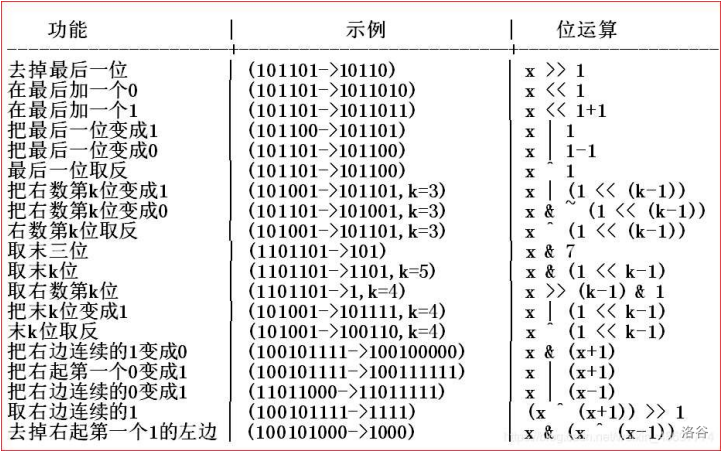
1.概述
用01数字标志状态
2.要求
-
对象状态只能有两种,例如放/不放,正/反等等
-
某一项指标的范围很小
3.实际运用
后续\(S_i\)一般表示状态(除特殊说明)
特殊方格棋盘
组合:我会!\(n!\)
先考虑所有格子都能放
\(n \leqslant 20\),可以状压
\(0\)表示没放,\(1\)表示放了
由于位运算的尿性,最右边是第一列,从右往左算
对于状态\(01101\),就表示放了\(1,3,4\)列
由于一行只能放一个,上述状态表示第三行,那么
更进一步的,对于数\(s\),如果某一位是\(1\),那么就可以从这一位为0的状态转移而来
用位运算就是:
答案就是\(f(11111) = f(2^n-1)\)
但有的格子不能放了
那么首先,我们把不能放的状态也压缩
比如\(a[3]=00100\)就表示第三行第三列不能放
然后对于枚举的状态\(s\),进行如下操作:
解释:\(a_i\)取反后被标记为不能放的列一定是\(0\),再按位与就让\(s\)中同列的位置也变为\(0\),就相当于不能放
更多的,对于快速求得哪一位是\(1\),可以使用\(lowbit\) 啊?
for(int i = 1;i <= m;i++)
{
scanf("%d%d",&x,&y);
a[x] |= (1 << (y - 1));// 把不能放的位置标记为1
}
f[0] = 1;
//cout << 114 << endl;
for(int i = 1;i <= res;i++)
{
int u,num = 0;
for(u = i;u;u -= lowbit(u)) num++;//统计1的个数,也就是当前的i表示第几行
u = i & (~a[num]);//把不能放的位置变成0
while(u)
{
//cout << 114 << endl;
//用lowbit提取u中的1,即100...
f[i] += f[i ^ lowbit(u)];// 只有i的这一列不为1才能加
u -= lowbit(u);
}
}
P1879 [USACO06NOV] Corn Fields G
首先将能不能种草压缩
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= m;j++)
{
int x;
scanf("%d",&x);
a[i] = (a[i] << 1) + x;
}
}
设\(dp_{i,s}\)表示第\(i\)行状态为\(S\)时的方案数
对于枚举的状态\(S\),如果存在\(11\)之类的非法情况,那么
为了避免上下相邻,我们取得\(i-1\)行的状态\(S'\),如果上下相邻,那么二者必有一位均是1,即
方程就是
for(int i = 1;i <= n;i++)
{
for(int j = 0;j <= (1 << m) - 1;j++)
{
int u = j;
if(u & (u << 1)) continue;//排除左右相邻
if(a[i] == (a[i] | u))
{
vis[i][u] = 1; //标记合法,留着后面取用
for(int k = 0;k <= (1 << m) - 1;k++)
{
if(k & (k << 1)) continue;
int v = k;
if(!vis[i - 1][v]) continue;//不合法
if(u & v) continue;//排除上下相邻
dp[i][u] = (dp[i][u] + dp[i - 1][v]) % mod;
}
}
}
}
P1896 [SCOI2005] 互不侵犯
用\(0/1\)表示有没有放国王
设\(dp_{i,j,S}\)表示放到第\(i\)行,用了\(j\)个国王,第\(i\)行的状态为\(S\)
接下来看转移条件
如果一个国王在第\(i\)行放在了第\(j\)列,那么对第\(i + 1\)行来说,第\(j - 1,j,j + 1\)列均不能放国王
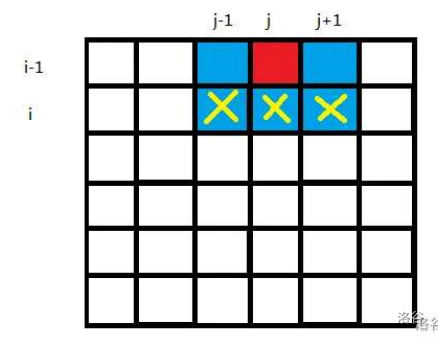
接下来考虑用位运算排除情况
设当前第\(i\)行状态为\(S_i\),上一行状态为\(S_{i-1}\)
如果第\(j-1\)列有国王,可以右移一下
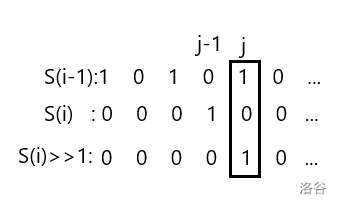
类似可得:
第\(j\)列有国王:\(S_i \& S_{i-1} = 1\)
第\(j + 1\)列有国王:\((S_i << 1)\&S_{i-1} = 1\)
转移条件就是上述三个式子的值均不为1
考虑方程式
发现前两维很像背包
第\(i\)行放的棋子就是\(S_i\)中\(1\)的个数,设为\(num_{S_i}\)
初始化:\(dp_{0,0,0} = 1\)
技巧:我们可以预处理出来一堆左右不相邻的合法状态备用,可以避免盲目暴力
P2704 [NOI2001] 炮兵阵地
又一道经典的入门题
放为\(1\),不放为\(0\)
根据炮兵射程可得
- 连续三格内只能有一个阵地
横向判定就是分别左移一位和两位再分别取与
纵向判定涉及到三行,所以\(dp\)中要多一些行的状态
设\(dp_{i,S_i,S_j}\)表示到了第\(i\)行,当前行的状态是\(S_i\),上一行的状态是\(S_j\)
那么转移就是\(dp_{i-1,S_j,S_k} \to dp_{i,S_i,S_j}\),判定的三行分别是\(S_i,S_j,S_k\)
由于连续三格在同一列,所以直接取与就行
转移方程:
取答案时要遍历所有可能状态
由于第一、二行上面不足两行,需要单独处理
for(int i = 1;i <= tot;i++)
{
if((a[1] | S[i]) == a[1])
{
vis[1][S[i]] = 1;
dp[1][S[i]][0] = num[S[i]];
}
}//第一行,就是初始化
for(int i = 0;i <= tot;i++)
{
if((a[2] | S[i]) == a[2])
{
int si = S[i];
vis[2][S[i]] = 1;
for(int j = 0;j <= tot;j++)
{
int sj = S[j];
if(!vis[1][sj]) continue;
if((si & sj) == 0)
dp[2][si][sj] = max(dp[2][si][sj],dp[1][sj][0] + num[si]);
}
}
}//第二行
for(int r = 3;r <= n;r++)
{
for(int i = 0;i <= tot;i++)//第r行状态
{
int si = S[i];
if((a[r] | si) == a[r])
{
vis[r][si] = 1;
for(int j = 0;j <= tot;j++)//第r-1行状态
{
int sj = S[j];
if(!vis[r - 1][sj]) continue;
if(si & sj) continue;
for(int k = 0;k <= tot;k++)//第r-2行状态
{
int sk = S[k];
if(!vis[r - 2][sk]) continue;
if(((sj & sk) | (si & sk)) == 0)
dp[r][si][sj] = max(dp[r][si][sj],dp[r - 1][sj][sk] + num[si]);
}
}
}
}
}
int ans = -1;
for(int i = 1;i <= tot;i++)
for(int j = 1;j <= tot;j++)
ans = max(ans,dp[n][S[i]][S[j]]);//遍历所有情况
- \(Tip:\)为了避免内存危机,可以定义\(dp_{i,j,k}\)为当前为第\(i\)行,该行状态是合法状态中的第\(j\)个,上一行是合法状态中的第\(k\)个
把代码中的\(si,sj,sk\)改成\(i,j,k\)就行
P3226 [HNOI2012] 集合选数
乍一看wc这是状压?
我们只能用\(01\)表示选没选,不能知道具体内容,所以对于二倍三倍的要求是很难办到的
那么我们能否想一个办法,使得当第\(i\)位为\(1\),第\(2i\)、\(3i\)位就自动不可能为\(1\)了呢
也就是说,这种构造下的每一次选择伴随着舍弃两个选择
这种构造其实早就见过——
棋类问题
这种问题就是在某处放了棋后自动舍弃掉了会被攻击到的格子,符合需求
所以考虑构造一个矩阵来实现类似下棋的操作
不妨把二倍放到右边,三倍放到下边,就是
设定一个棋子的攻击范围就是它的右边和下边,那么问题就转化成了有多少合法放棋方案
但这样有一个问题:比如\(n = 20\)
一些数进不去,一些位置空着
再次类比棋盘问题,我们还做过特殊方格棋盘,就把空位设置成不能放置棋子来解决
进不去的数呢?
再多搞几个棋盘,不在同一个棋盘上的数一定互不影响,所以合法
这样问题就成了
有若干张棋盘,每张棋盘上都有格子不能放棋,现在要在每个棋盘上放置若干枚棋子,满足所有棋子不能互相攻击到(当然,不在一个棋盘上的棋子肯定不能互相攻击)攻击范围就是右和下,求合法方案数
对于每张棋盘使用状压求解,使用乘法原理联结各个棋盘的答案得到方案数
绝了
坑点:memset会超时四个
预处理:
void init(int x)
{
//不同于dp,这里面全是赋值类操作,所以不用memset
r = 0;
for(int i = 1;i <= 20;i++)
{
if(i == 1) a[i][1] = x;//特殊处理左上角
else a[i][1] = a[i - 1][1] * 3;
if(a[i][1] > n) break;
vis[a[i][1]] = 1;//标记数字已被放入某个棋盘
r = i;//记录最大行数,dp要用
int num = 1;
for(int j = 2;j <= 20;j++)
{
a[i][j] = a[i][j - 1] * 2;
if(a[i][j] > n) break;
num = j;
vis[a[i][j]] = 1;
}
maxx[i] = (1 << num) - 1;//这里记录的是每行的上限,就是每行有多少个连续的1(可放棋子的位置)
}
}
每个棋盘的dp:
```cpp
ll getans()
{
//S[i]是预处理的合法状态
for(int i = 1;S[i] <= maxx[1];i++) dp[1][i] = 1;//合法状态不能超过极限
for(int i = 2;i <= r;i++)
{
for(int j = 1;S[j] <= maxx[i] && j <= tot;j++)
{
dp[i][j] = 0;//由于不能使用memset,就用一个清零一个
for(int k = 1;S[k] <= maxx[i - 1] && k <= tot;k++)
{
if(S[j] & S[k]) continue;
dp[i][j] = (dp[i][j] + dp[i - 1][k]) % mod;//朴素的dp
}
}
}
ll res = 0;
for(int i = 1;S[i] <= maxx[r];i++)
res = (res + dp[r][i]) % mod;
return res;
}
联结答案:
for(int i = 1;i <= n;i++)
{
if(!vis[i]) //未使用,就构建新棋盘
{
init(i);
ll sum = getans();
ans = ans * sum % mod;//乘法原理
}
}
可见状压的一大基础模型就是棋盘类问题,这也是状压最本质的呈现
接下来看一些脱离棋盘的问题:
P2831 [NOIP2016 提高组] 愤怒的小鸟
写这题前趴电脑前面睡了半个小时,可能是被状压NaOH的昏迷了
\(n\leqslant 18\),考虑用\(0,1\)表示猪的死活,\(0\)表示没死,\(1\)表示死了
设\(dp_{S}\)表示达到状态\(S\)所需的最少鸟数
那么
显然,死的猪复活不了,所以\(S'\)中\(1\)的个数在\(S\)的基础上要多,设多出来\(k\)个\(1\),那么\(num_{S'}\)就表示打死那\(k\)只猪所需的最少鸟数
更具体的,由于抛物线的形式,所以两个点就能确定一个抛物线,那么设\(P_{i,j}\)表示经过第\(i,j\)个点能杀死的猪的集合,和\(S\)相同,杀死的猪在\(P_{i,j}\)中对应的数位为\(1\)
那么
但也可能存在需要额外消耗一只鸟(说明过这个点的抛物线上只有一个点\(k\))的情况,还得再处理一下
接下来考虑一些细节
- 求\(P_{i,j}\)
设\((x_1,y_1),(x_2,y_2)\)在同一条抛物线上,那么
解得
int init(int p,int q)
{
double x1 = point[p].x,x2 = point[q].x;
double y1 = point[p].y,y2 = point[q].y;
if(x1 == x2) return 0;//会导致a变成nan
double a = (y1 * x2 - y2 * x1) / (x1 * x2 * x1 - x1 * x2 * x2);
double b = (y1 * x2 * x2 - y2 * x1 * x1) / (x1 * x2 * x2 - x1 * x2 * x1);
//cout << a << endl;
if(a >= 0) return 0;//题目要求
int s = 0;
for(int i = 1;i <= n;i++)
{
double x = point[i].x,y = point[i].y;
if(fabs(a * x * x + b * x - y) < eps)//实数误差在允许范围内
{
s |= 1 << (i - 1);
dp[s] = dp[1 << (i - 1)] = 1;//当前的猪和目前找到的在一条线上的猪都能用一只鸟打掉
}
}
return s;
}
- 跳过不必要的枚举
我们需要一个\(i\)来枚举状态,需要\(j,k\)枚举\(P_{j,k}\),总复杂度是\(O(Tn^2\times(2^n-1))\),极限\(2e9,\)可能会超时(这么说是因为不加此处的优化好像也能过)
显然,使用\(P_{j,k}\)的前提就是第\(j,k\)只猪都活着,所以得保证当前\(i\)的第\(j,k\)位均不为\(1\)
for(int i = 0;i <= (1 << n) - 1;i++)
{
for(int j = 1;j <= n;j++)
{
if((i >> (j - 1)) & 1 == 1) continue; //第j只猪是活的
for(int k = 1;k <= j;k++)
{
if((i >> (k - 1)) & 1 == 1) continue;//第k只猪是活的
dp[i | S[j][k]] = min(dp[i | S[j][k]],dp[i] + 1);
}
dp[i | (1 << (j - 1))] = min(dp[i | (1 << (j - 1))],dp[i] + 1);
}
}
我才不说那个把\(double\)老写成\(int\)的傻子是谁 (我)
P4163 [SCOI2007] 排列
\(|s| \leqslant 10\),状压字符串
用\(01\)表示某一位数字有没有被使用,\(0\)表示没用,\(1\)表示用了
接下来定义\(dp\)状态
发现“整除”这个东西挺不好保证的,尤其是在只知道位的情况下更不好办了
为了解决这个问题,不妨引进余数,整除就是余数为\(0\)的情况
故设\(dp_{S,d}\)表示状态为\(S\),余数为\(d\)时的方案数
如果要使用第\(i\)个数,那么根据\(dp\)尿性,前\(i-1\)位已经排好(但具体数字可能不是前\(i-1\)个数),应当放到第\(i\)位(从右往左),那么由余数可加性可得新余数就是\((10\times j + s_i) \% d\),其中\(j\)就是前 \(i-1\)位模\(d\)的余数
所以得到方程
由上一道题可知第\(i\)位必须是\(0\)
坑点:需要对序列去重,或者打标记防重复
if(vis[c[j] - '0']) continue;//该数字已被使用
if(i & (1 << (j - 1))) continue;//第j位被用了
vis[c[j] - '0'] = 1;//打标记
P2167 [SDOI2009] Bill的挑战
\(N \leqslant 15\),状压每个字符串是否与\(T\)匹配,\(1\)表示配上了,\(0\)表示没配上
很明显,状态中最多只能有\(K\)个\(1\)
但有些\(S\)是一定不能同时匹配上一个\(T\)的,可以预处理
接下来就是定义\(dp\)状态
\(dp\)中至少有一维是\(S\),考虑另一位放什么
由于每一位放不同的字母会产生不同的效果,所以考虑用一维枚举放到了第几位
所以得到\(dp_{i,S}\)表示当前在第\(i\)位,匹配状态为\(S\)的方案数
答案就是
方程就是
接下来细嗦预处理并具体化\(dp\)
设\(vis_{i,j}(1\leqslant j \leqslant 26)\)表示第\(i\)位放了第\(j\)个字符时仅第\(i\)列的匹配情况(\(01\)表示)
for(int i = 1;i <= l;i++)
{
for(int j = 1;j <= 26;j++)
{
for(int k = 1;k <= n;k++)
{
char op = s[k][i];
if(op == '?') vis[i][j] |= (1 << (k - 1));
else
{
if(op - 'a' + 1 == j) vis[i][j] |= (1 << (k - 1));
else continue;
}
}
}
}
那么结合\(dp\)可得
按位与就表示只有前\(i-1\)位配上了(\(S\)对应位为\(1\))并且第\(i\)位也能配上(\(vis[i][j]\)对应位为\(1\))该串状态才可能为\(1\)
初始化:\(dp_{0,2^n-1} = 1\)
dp[0][(1 << n) - 1] = 1;
for(int i = 1;i <= l;i++)
for(int s = 0;s <= (1 << n) - 1;s++)
for(int j = 1;j <= 26;j++)
dp[i][s & vis[i][j]] = (dp[i][s & vis[i][j]] + dp[i - 1][s]) % mod;
听说还有容斥做法,。先咕咕
Disease Management
好像比前面都裸
把每头牛的得病状态压缩,类似上面的方程,把与改成或就行
坑点:二维要先继承上一维的状态再\(dp\)
for(int i = 1;i <= n;i++)
{
for(int s = 0;s <= (1 << d) - 1;s++)
{
dp[i][s] = dp[i - 1][s];//先继承
dp[i][s | a[i]] = max(dp[i][s | a[i]],dp[i - 1][s] + 1);
}
}
P3451 [POI2007] ATR-Tourist Attractions
图论+dp
题面有点扯淡
原题翻译核心:
最短的方案是\(1\to2\to4\to3\to4\to5\to8\),总长度为19,注意FGO为了从城市2到城市3可以经过城市4(\(2\to4\to3\)),但不在城市4停留
清新了
也就是说,\(2\to4\to3\)两条道路(边) 可以变成\(2\to3\)这一条路径
这样一来,我们就可以使用最短路算法处理出\(2\sim k+1\)到其他点的最短路并记录,相当于用\(2\sim k+1\)建了个新图,每一条边都是最短路径 (最小生成图)
设\(d_{i,j}\)表示从\(i\)到\(j\)的最短路径
建了新图之后,就只剩下了\(1 \sim k + 1,n\)等关键点,刚好\(K \leqslant 20\),直接状压这些点走没走
接下来考虑预处理\(g\)个限制
这一点可以参考集合选数,把每一个点的“上限”状态处理出来
设\(dp_{i,S}\)表示当前在\(i\),状态为\(S\)的最短路
首先新图联通,所以点两两可达,直接暴力枚举
假设要从\(j\)走到,那么\(i\)就要满足
-
对应数位为\(0\)
-
要在\(i\)之前停留的数对应的数位均为\(1\)
那么
其中
答案统计:
一交一片黑,发现————
内存危机:64MB!!!
我突然释怀的亖了
是时候拿出我不会的必杀技了————————
滚动数组
我们发现第二维按照原开法最大是\(1 << (k + 1)-1\),但这之中有很多冗余状态,考虑优化
显然,如果\(S\to S_1 \to S_2 \to...\)成立,那么状态中\(1\)的数量一定单调增(旧的点走过了,不断在走新的点)
进一步的,相邻的转移状态中间\(1\)的个数一定只差了\(1\),因为一次只能走一个点
所以可以只存储相邻两层的信息,上一层是含有\(i\)个\(1\)的方案,下一层就是含有\(i+1\)个\(1\)的方案
就是开成\(dp_{i,S,2}\),用异或跳层数
中间\(S\)的大小取决于该层状态含\(1\)的个数,如果含有\(x\)个\(1\),那么最大就是\(C_{20}^{x}\)
显然,最大是\(C_{20}^{10} = 184756\)
相比\(2^{20}-1=1048575\)是极大地优化
//由于题目特点,提前k++了
//这里将点的编号统一-2是方便与位运算兼容,直接压的是2~k+1
for(int i = 0,num,now;i < 1 << (k - 1);i++)
{
for(num = 0,now = i;now;now -= lowbit(now),num++);
newadd(num,i);
id[i] = ++ sum[num];
}//用前向星的方式将含1个数与对应集合连接起来
for(int p = h[1];p;p = Re[p].ne)//遍历含1个1的集合
{
int v = Re[p].to;
for(int i = 2;i <= k;i++)
{
if(v & (1 << (i - 2)))
{
dp[i][id[v]][0] = d[i][1];
break;
}
}
}
//方向:j->i
for(int num = 2;num < k;num++,l ^= 1/*l控制层数*/)
{
for(int o = h[num];o;o = Re[o].ne)
{
int v = Re[o].to;
for(int i = 2,now;i <= k;i++)
{
if((v & (1 << (i - 2))) && ((S[i] & v) == S[i]))//判断是否满足条件
{
now = v ^ (1 << (i - 2));//j循环中i点还没走过
dp[i][id[v]][l] = 1 << 30;
for(int j = 2;j <= k;j++)
{
if((now & (1 << (j - 2))) && ((S[j] & now) == S[j]))
dp[i][id[v]][l] = min(dp[i][id[v]][l],dp[j][id[now]][l ^ 1] + d[j][i]);
}
}
}
}
}
for(int o = h[k - 1];o;o = Re[o].ne)
{
int v = Re[o].to;
for(int i = 2;i <= k;i++)
{
if((v & (1 << (i - 2))) && ((S[i] & v) == S[i]))
ans = min(ans,dp[i][id[v]][l ^ 1] + d[i][n]);
}
}//走完所有关键点后前往n点
P3622 [APIO2007] 动物园
先明确状压什么
发现题目中唯一的较小值是“连续的5个围栏”,考虑状压连续的5个围栏的状态
套路的设出\(dp_{i,S}\)。第一维表示当前所在围栏,第二维表示\(i\sim i + 4\)这5个围栏的状态,\(0\)表示移走,\(1\)表示还在,由\(dp_{i - 1,S'}\)转移答案
由于重叠关系,\(S\)确定后,\(i\sim i + 4\)位均已知,只有第 \(i-1\) 位是放/不放,在此处比个 \(max\)后加上 \(S\)能使有多少孩子开心
接下来考虑\(S'\)和\(S\)的关系
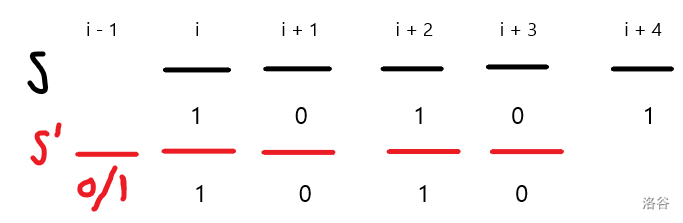
\(S'\)的后四位就是\(S\)的前四位,即\(S >> 1\),所以如果第\(i - 1\)位放就是
不放的话就不按位或了
所以
显然\(num\)可以预处理
仿照dp数组定义\(num_{i,S}\)表示\(i\sim i + 4\)的围栏状态为\(S\)时高兴的小朋友个数
我们尝试把小孩儿的喜恶也压成一个五位的二进制,但每个动物有三种状态:喜欢,讨厌,和无感
那就设置两个数\(x,y\),一个压喜欢,一个压不喜欢,共同点就是有感为1,无感为0,位数对应要和dp式兼容不然会出问题
但是考虑到转圈,沿用石子合并旧法,小于\(E\)的多加一个\(n\)即可
void init()
{
int li,dis;
li = 0;
dis = 0;
for(int i = 1;i <= f;i++)
{
int x;
scanf("%d",&x);
if(x < e) x += n;
int u = 5 - (x - e);
li |= 1 << (u - 1);//dp式的位是从左至右,但是位运算是从右往左,要转换
}
for(int i = 1;i <= l;i++)
{
int x;
scanf("%d",&x);
if(x < e) x += n;
int u = 5 - (x - e);
dis |= 1 << (u - 1);
}
for(int s = 0;s <= 31;s++)
{
bool f1 = (s & li);//要求对应位至少有一个1
bool f2 = ((~s) & dis);//要求对应位至少有一位是0,所以先取反
if(f1 || f2) num[e][s]++;
}
}
初始化:限定\(0\sim 4\)的状态,对于每个状态做一次dp
坑点:限定\(0\sim 4\)就是限定了\(n,1,2,3,4\),所以取答案时不能遍历
int u = (1 << 4);
int ans = -1;
for(int S = 0;S <= 31;S++)//0-4位的状态
{
memset(dp[0],-inf,sizeof(dp[0]));//其他状态0初始化为极小值
dp[0][S] = 0;//当前状态初始
for(int i = 1;i <= n;i++)
for(int s = 0;s <= 31;s++)
dp[i][s] = max(dp[i - 1][(s >> 1)],dp[i - 1][(s >> 1) | u]) + num[i][s];
//for(int s = 0;s <= 31;s++)//不遍历
ans = max(ans,dp[n][S]);//终末状态就是限定的初始态
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号